Conservative Vector Fields

Theorem. If $\vec{F} = (P(x,y), Q(x,y))$ is a vector field in the plane, and P and Q have continuous partial derivatives on a region. the following four statements are equivalent:

1. $\vec{F} = \nabla f$ for some function $f(x,y)$ .

2. $\pder Q x = \pder P y$ .

3. If $\sigma$ is a closed curve lying in the region --- i.e. a path which starts and ends at the same point --- then

$$\int_{\sigma} \vec{F}\cdot \bvec{ds} = 0.$$

4. ( Path independence) If $\sigma$ and $\tau$ are paths in the region which start at the same point and end at the same point, then

$$\int_{\sigma} \vec{F}\cdot \bvec{ds} = \int_{\tau} \vec{F}\cdot \bvec{ds}.$$

To say that these statements are equivalent means that if one of them is true, then all of them are true (and if one of them is false, all of them are false). A field that satisfies any one of these conditions is a conservative field --- or sometimes a gradient field, or sometimes path independent.

Before I show that these statements are equivalent, I'll give a couple of examples.

Example. Show that $\vec{F} = (2 x + y, x + 2 y)$ is a gradient field.

I want a function f such that $\grad f = (2 x + y, x + 2 y)$ , i.e.

$$\pder f x = 2 x + y \quad\hbox{and}\quad \pder f y = x + 2 y.$$

Integrate the first equation with respect to x:

$$f = \int (2 x + y)\,dx = x^2 + x y + C(y).$$

Since the integral is with respect to x, y is constant, and must be included in the arbitrary constant --- hence $C(y)$ . Differentiate with respect to y and set the result equal to $\pder f y$ above:

$$x + 2 y = \pder f y = 0 + x + \der C y.$$

I get $\der C y = 2 y$ , so $C = y^2 + D$ . This time, D is a numerical constant. Since the derivative of a number is 0, and since I just want some potential function (see the previous example), I might as well take $D = 0$ . Then $C = y^2$ , so

$$f = x^2 + x y + y^2.\quad\halmos$$

Thus, if $f(x, y) = x^2 + x y + y^2$ , then

$$\pder f x = 2 x + y, \quad \pder f y = x + 2 y.$$

Definition. A function f such that $\nabla f = \vec{F}$ is called a potential function for $\vec{F}$ .

Example. Let $\vec{F} = (2 x + y, x + 2 y)$ and

$$\sigma(t) = (\cos t, \sin t), \qquad 0 \le t \le 2 \pi.$$

Show that

$$\int_{\sigma} \vec{F} \cdot \bvec{ds} = 0.$$

The velocity vector is

$$\sigma\,'(t) = (-\sin t, \cos t).$$

The field is

$$\vec{F}(t) = (2 \cos t + \sin t, \cos t + 2 \sin t).$$

Hence,

$$\vec{F}(t) \cdot \sigma\,'(t) = -2 \cos t \sin t - (\sin t)^2 + (\cos t)^2 + 2 \cos t \sin t = (\cos t)^2 - (\sin t)^2 = \cos 2 t.$$

So

$$\int_{\sigma} \vec{F} \cdot \bvec{ds} = \int_0^{2 \pi} \cos 2 t\,dt = \left[\dfrac{1}{2} \sin 2 t\right]_0^{2 \pi} = 0.$$

Theorem. Suppose $\vec{F} = \nabla f$ is a gradient field, and let $\sigma(t)$ for $a \le t \le b$ be a path. Then

$$\int_{\sigma} \vec{F} \cdot \bvec{ds} = f\left(\sigma(b)\right) - f\left(\sigma(a)\right).$$

In other words, to evaluate the integral of a gradient field, just plug the endpoints of the path ($\sigma(a)$ and $\sigma(b)$ ) into the potential function (f).

$$\hbox{\epsfysize=1.75 in \epsffile{conservative-fields-1.eps}}$$

Proof. By the Chain Rule,

$$D(f \cdot \sigma)(t) = Df\left(\sigma(t)\right) \cdot \sigma\,'(t) = \nabla f\left(\sigma(t)\right) \cdot \sigma\,'(t) = \vec{F}\left(\sigma(t)\right) \cdot \sigma\,'(t).$$

So

$$\int_{\sigma} \vec{F} \cdot \bvec{ds} = \int_a^b \vec{F}\left(\sigma(t)\right) \cdot \sigma\,'(t)\,dt = \int_a^b D(f \cdot \sigma)(t)\,dt.$$

The antiderivative of the derivative of $f \cdot \sigma$ is just $f \cdot \sigma$ , so

$$\int_a^b D(f \cdot \sigma)(t)\,dt = \left[f \cdot \sigma(t)\right]_a^b = f\left(\sigma(b)\right) - f\left(\sigma(a)\right).$$

All together,

$$\int_{\sigma} \vec{F} \cdot \bvec{ds} = f\left(\sigma(b)\right) - f\left(\sigma(a)\right).\quad\halmos$$

Example. Compute $\displaystyle \int_{\sigma} 2 x y\,dx + x^2\,dy$ , where

$$\sigma(t) = ((\cos t)^3, (\sin t)^3), \quad 0 \le t \le \dfrac{\pi}{2}.$$

To compute this directly, you would need to do the integral

$$\int_0^{\pi/2} \left(-6 (\cos t)^5 (\sin t)^4 + 3 (\cos t)^4 (\sin t)^2\right)\,dt.$$

Yuck.

Instead, notice that if $f(x, y) = x^2 y$ , then $\nabla f = (2 x y, x^2)$ , which is the field in the integral. Hence, I can compute the integral by plugging the endpoints of the path into f.

$$\sigma(0) = (1, 0) \quad\hbox{and}\quad \sigma\left(\dfrac{\pi}{2}\right) = (0, 1).$$

So

$$\int_{\sigma} 2 x y\,dx + x^2\,dy = f(0, 1) - f(1, 0) = 0.$$

(The fact that it comes out to 0, as opposed to a nonzero number, is a coincidence.) The important thing to notice is how easy it was to do the computation!

Now I will go back and prove that the four statements which define a conservative field are equivalent. To prove that they're equivalent, I must show that any one of them follows from any other. I will do it this way:

$$\hbox{statement 1} \quad \ifthen \quad \hbox{statement 2} \quad \ifthen \quad \hbox{statement 3} \quad \ifthen \quad \hbox{statement 4} \quad \ifthen \quad \hbox{statement 1}$$

Proof. First, assume statement 1 is true, so $\vec{F} = \nabla f$ for some f. Since $\vec{F} = (P, Q)$ , this means that

$$P = \pder f x, \quad Q = \pder f y.$$

Hence,

$$\pder P y = \dfrac{\partial^2 f}{\partial y \partial x}, \quad \pder Q x = \dfrac{\partial^2 f}{\partial x \partial y}.$$

But the two second derivatives are equal by equality of mixed partials, so $\pder Q x = \pder P y$ . This is statement 2.

Next, assume statement 2 is true, so $\pder Q x = \pder P y$ . Take a closed curve $\sigma$ . I want to show that the integral around $\sigma$ is 0. This follows from Green's theorem, which I'll discuss in more detail later. For now, note that the closed curve $\sigma$ encloses a region R.

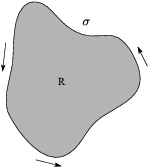
$$\hbox{\epsfysize=1.5 in \epsffile{conservative-fields-2.eps}}$$

Green's theorem says

$$\int_{\sigma} \vec{F} \cdot \bvec{ds} = \int_{\sigma} P\,dx + Q\,dy = \dint_R \left(\pder Q x - \pder P y\right)\,dx\,dy.$$

But the double integral on the right is 0, because $\pder Q x = \pder P y$ . Therefore, the integral around a closed curve is 0, and that is statement 3.

Before I do the next step, here is some notation. If $\sigma$ is a curve, $-\sigma$ will denote the same curve traversed in the opposite direction.

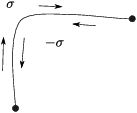
$$\hbox{\epsfysize=1 in \epsffile{conservative-fields-3.eps}}$$

If I traverse a curve backward, the line integral flips its sign:

$$\int_{-\sigma} \vec{F} \cdot \bvec{ds} = -\int_{\sigma} \vec{F} \cdot \bvec{ds}.$$

Now assume statement 3 is true: The line integral around a closed curve is 0. Take curves $\sigma$ and $\tau$ , both of which start at P and both of which end at Q. I need to show that

$$\int_{\sigma} \vec{F} \cdot \bvec{ds} = \int_{\tau} \vec{F} \cdot \bvec{ds}.$$

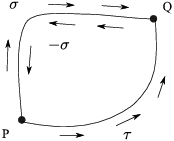
$$\hbox{\epsfysize=1.25 in \epsffile{conservative-fields-4.eps}}$$

If I go from P to Q along $\tau$ then back from Q to P along $-\sigma$ , I have a closed curve. So the integral around $\tau + (-\sigma)$ is 0:

$$\int_{\tau + (-\sigma)} \vec{F} \cdot \bvec{ds} = 0.$$

Do each path separately:

$$\int_{\tau} \vec{F} \cdot \bvec{ds} + \int_{-\sigma} \vec{F} \cdot \bvec{ds} = 0.$$

The second integral is the negative of the integral along $\sigma$ :

$$\int_{\tau} \vec{F} \cdot \bvec{ds} - \int_{\sigma} \vec{F} \cdot \bvec{ds} = 0.$$

Finally, move the second integral to the other side:

$$\int_{\tau} \vec{F} \cdot \bvec{ds} = \int_{\sigma} \vec{F} \cdot \bvec{ds}.$$

This is what I wanted to prove, so statement 4 follows from statement 3.

Finally, suppose statement 4 is true: The field is path independent. I want to show that $\vec{F} = (P, Q)$ is a gradient field. I need to find a function f such that $\nabla f = \vec{F}$ . To do this, take any path $\sigma$ from $(0, 0)$ to $(x, y)$ and define

$$f(x, y) = \int_{\sigma} \vec{F} \cdot \bvec{ds}.$$

By path independence, it does not matter what path I choose, so I'll use the path from $(0, 0)$ to $(x, 0)$ to $(x, y)$ made up of two segments as shown below:

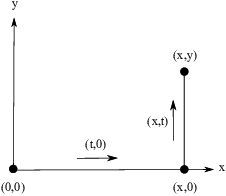
$$\hbox{\epsfysize=1.75 in \epsffile{conservative-fields-5.eps}}$$

Having defined f using this path, I have to show that $\pder f x = P$ and $\pder f y = Q$ .

The horizontal part is $\sigma(t) = (t, 0)$ for $0 \le t \le x$ . The velocity vector is $\sigma\,'(t) = (1, 0)$ , and $\vec{F}(t) = (P(t, 0), Q(t, 0))$ . So

$$\vec{F} \cdot \sigma\,'(t) = P(0, t).$$

Therefore, the integral for the horizontal segment is

$$\int_0^x P(0, t)\,dt.$$

The vertical part is $\tau(t) = (x, t)$ for $0 \le t \le y$ . The velocity vector is $\tau\,'(t) = (0, 1)$ and $\vec{F}(t) = (P(x, t), Q(x, t))$ . So

$$\vec{F} \cdot \tau\,'(t) = Q(x, t).$$

Therefore, the integral for the vertical segment is

$$\int_0^y Q(x, t)\,dt.$$

The line integral along the whole path --- which by definition is f --- is

$$f(x, y) = \int_0^x P(0, t)\,dt + \int_0^y Q(x, t)\,dt.$$

Remember that I was trying to show that $\pder f x = P$ and $\pder f y = Q$ . Differentiate the last equation with respect to y.

$$\pder f y = \pder {} y \int_0^x P(0, t)\,dt + \pder {} y \int_0^y Q(x, t)\,dt.$$

The first integral only involves x, so its derivative with respect to y is 0. For the second integral, apply the Fundamental Theorem of Calculus: The y in the top limit replaces the t in the integrand and I get $Q(x, y)$ . So

$$\pder f y = Q(x, y).$$

That is, f has the right y derivative.

If you take a path made up of two segments going from $(0, 0)$ to $(0, y)$ to $(x, y)$ --- along the y-axis, then horizontally --- you can show in similar fashion that $\pder f x = P$ . (Remember that I get the same "f" regardless of which path I take.) Thus,

$$\nabla f = \left(\pder f x, \pder f y\right) = (P, Q) = \vec{F}.$$

This proves statement 1.

And that finishes the proof that the four statements are equivalent.

By the way, the last part of the proof gives a way of constructing a potential function for a gradient field. It's perhaps not the best way for a human being to do this, but would be a reasonable approach if you were doing this on a computer.

Example. Find a potential function for $\vec{F} = \langle 2 x y, x^2)$ using the line integrals in the proof of the theorem.

I can find f using the formula

$$f(x, y) = \int_0^x P(0, t)\,dt + \int_0^y Q(x, t)\,dt.$$

Here $P = 2 x y$ , so $P(0, t) = 0$ . Likewise, $Q = x^2$ , so $Q(x, t) = x^2$ . So

$$f(x, y) = 0 + \int_0^y x^2\,dt = \left[x^2 t\right]_0^y = x^2 y.$$

By the way, notice that $g = x^2 y + 143$ is also a potential function for this field, since $\pder g x = 2 x y$ and $\pder g y = x^2$ . There are infinitely many potential functions for a gradient field; they differ by a numerical constant.

So far, I've discussed vector fields in $\real^2$ , that is, 2 dimensions. There are few surprises when you move up to 3 dimensions.

Theorem. Let $\vec{F} = (f_1, f_2, f_3)$ be a 3-dimensional vector field, and assume its components have continuous partial derivatives. Then the following four statements are equivalent:

1. $\vec{F} = \nabla f$ for some function $f(x, y)$ .

2. $\curl \vec{F} = \vec{0}$ .

3. If $\sigma$ is a closed curve --- i.e. a path which starts and ends at the same point --- then

$$\int_{\sigma} \vec{F} \cdot \bvec{ds} = 0.$$

4. ( Path independence) If $\sigma$ and $\tau$ are paths which start at the same point and end at the same point, then

$$\int_{\sigma} \vec{F} \cdot \bvec{ds} = \int_{\tau} \vec{F} \cdot \bvec{ds}.$$

Once again, a field that satisfies any one of these conditions is a conservative field --- or sometimes a gradient field, or sometimes path independent.

The only change in moving from 2 dimensions to 3 dimensions is in statement 2. To see how this is related to the $\pder Q x = \pder P y$ for a 2-dimensional field, take a field $\vec F = (P(x, y), Q(x, y))$ and regard it as a 3-dimensional field by making the third component 0, so

$$\vec{F} = \langle P(x, y), Q(x, y), 0).$$

Then

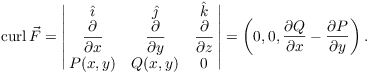
$$\curl \vec{F} = \left|\matrix{ \ihat & \jhat & \khat \cr \pder {} x & \pder {} y & \pder {} z \cr P(x, y) & Q(x, y) & 0 \cr}\right| = \left(0, 0, \pder Q x - \pder P y\right).$$

(Notice that, e.g., $\pder {} z P(x, y) = 0$ , because P does not contain any z's.) The condition $\curl \vec{F} = \vec{0}$ is, in this case, the same as $\pder Q x = \pder P y$ .

In fact, the components of $\vec{F}$ should have continuous first partials, except perhaps at finitely many points. Here's the reason I can allow finitely many "bad points" in this case but none in the 2-dimensional case.

Think of a closed curve as a piece of string. In a rough sense, the reason why the integral of a conservative field around a closed curve is 0 is that the string can be "reeled in" to the basepoint without changing the integral.

$$\hbox{\epsfysize=1.75 in \epsffile{conservative-fields-6.eps}}$$

When the curve has been reeled in to a single point, the integral over the curve is obviously 0.

In 2 dimensions, a curve can "get stuck" on a single bad point as you reel it in.

$$\hbox{\epsfysize=1.75 in \epsffile{conservative-fields-7.eps}}$$

However, if the picture above is in 3 dimensions, you can "lift" the curve up out of the plane and over the point in the middle, so the curve doesn't get stuck as you reel it in.

Example. Show that $\vec{F} = (2 x y + z, x^2 - 2 yz, -y^2 + 2 z + x)$ is conservative, and find a potential function for $\vec{F}$ .

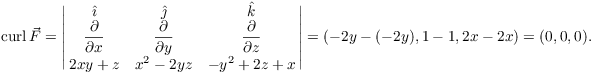
$$\curl \vec{F} = \left|\matrix{ \ihat & \jhat & \khat \cr \pder {} x & \pder {} y & \pder {} z \cr 2 x y + z & x^2 - 2 y z & -y^2 + 2 z + x \cr}\right| = (-2 y - (-2 y), 1 - 1, 2 x - 2 x) = (0, 0, 0).$$

Therefore, $\vec{F}$ is conservative. A potential function f must satisfy

$$\pder f x = 2 x y + z, \quad \pder f y = x^2 - 2 y z, \quad \pder f z = -y^2 + 2 z + x.$$

Integrate the first equation with respect to x:

$$f = \int (2 x y + z)\,dx = x^2 y + xdz + C(y,dz).$$

Since the integral is with respect to x, y and z are constant, and must be included in the arbitrary constant $C(y,z)$ . Now differentiate with respect to y and set the result equal to $\pder f y$ above:

$$x^2 - 2 y z = \pder f y = x^2 + \der C y.$$

I find that $\der C y = -2 y z$ , so integrating with respect to y,

$$C = \int (-2 y z)\,dy = -y^2 z + D(z).$$

This time, z is constant and must be included in the arbitrary constant $D(z)$ . Plug this back into f; it is

$$f = x^2 y + x z - y^2 z + D(z).$$

Finally, differentiate with respect to z and set the result equal to $\pder f z$ above:

$$-y^2 + 2 z + x = \pder f z = x - y^2 + \der D z.$$

I find that $\der D z = 2 z$ , so $D = z^2 + E$ , where E is a numerical constant. As in an earlier example, I may take $E = 0$ . This gives $D = z^2$ , so

$$f(x, y, z) = x^2 y + x z - y^2 z + z^2.\quad\halmos$$

Example. Compute $\displaystyle \int_{\sigma} \vec{F} \cdot \bvec{ds}$ , where

$$\vec{F} = (3 x^2 y - z^2, x^3 + 2, -2 x z + 1) \quad\hbox{and}\quad \sigma(t) = \left(t^4, \dfrac{2}{t + 1}, \cos \dfrac{\pi t}{2}\right), \quad 0 \le t \le 1.$$

You could compute the integral directly --- would you want to? There must be an easier way ...

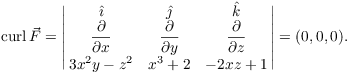
$$\curl \vec{F} = \left|\matrix{ \ihat & \jhat & \khat \cr \pder {} x & \pder {} y & \pder {} z \cr 3 x^2 y - z^2 & x^3 + 2 & -2 x z + 1 \cr}\right| = (0, 0, 0).$$

Since $\curl \vec{F} = \vec{0}$ , the field is conservative. If I can find a potential function, I can compute the integral by simply plugging the endpoints of the path into the potential function.

A potential function f must satisfy

$$\pder f x = 3 x^2 y - z^2, \quad \pder f y = x^3 + 2, \quad \pder f z = -2 x z + 1.$$

Integrate the first equation with respect to x:

$$f = \int (3 x^2 y - z^2)\,dx = x^3 y - x z^2 + C(y,z).$$

Since the integral is with respect to x, y and z are constant, and must be included in the arbitrary constant $C(y,z)$ . Now differentiate with respect to y and set the result equal to $\pder f y$ above:

$$x^3 + 2 = \pder f y = x^3 + \der C y.$$

I find that $\der C y = 2$ , so integrating with respect to y,

$$C = \int 2\,dy = 2 y + D(z).$$

This time, z is constant and must be included in the arbitrary constant $D(z)$ . Plug this back into f; it is

$$f = x^3 y - x z^2 + 2 y + D(z).$$

Finally, differentiate with respect to z and set the result equal to $\pder f z$ above:

$$-2 x z + 1 = \pder f z = -2 x z + \der D z.$$

I find that $\der D z = 1$ , so $D = z + E$ , where E is a numerical constant. As in an earlier example, I may take $E = 0$ . This gives $D = z$ , so

$$f = x^3 y - x z^2 + 2 y + z.$$

The endpoints of the path are

$$\sigma(0) = (0, 2, 1) \quad\hbox{and}\quad \sigma(1) = (1, 1, 0).$$

Therefore,

$$\int_{\sigma} \vec{F} \cdot \bvec{ds} = f(\sigma(1)) - f(\sigma(0)) = f(1, 1, 0) - f(0, 2, 1) = -2.\quad\halmos$$

Example. $\sigma$ is a path with positive components from a point P on $x y z = 1$ to a point Q on $x y z = 4$ . Compute $\displaystyle \int_{\sigma} \vec{F} \cdot \bvec{ds}$ , where

$$\vec{F} = \left(\dfrac{y z}{x y z + 1}, \dfrac{x z}{x y z + 1}, \dfrac{x y}{x y z + 1}\right).$$

The path isn't given --- in fact, its endpoints aren't given. Therefore, the path must not matter, i.e. the integral is probably path independent. In fact, $\vec{F} = \nabla f$ , for $f = \ln (x y z + 1)$ . Therefore,

$$\int_{\sigma} \vec{F} \cdot \bvec{ds} = f(Q) - f(P).$$

Now Q is on $x y z = 4$ , so for this point $x y z = 4$ . Likewise, P is on $x y z = 1$ , so for this point $x y z = 1$ . Hence,

$$f(Q) - f(P) = \ln (4 + 1) - \ln (1 + 1) = \ln 5 - \ln 2 = 0.91629 \ldots.\quad\halmos$$

Contact information

Bruce Ikenaga's Home Page

Copyright 2022 by Bruce Ikenaga