The Cross Product

The cross product of $\vec v = (v_1,v_2,v_3)$ and $\vec w = (w_1,w_2,w_3)$ is

$\vec v \times \vec w = (v_2 w_3 - v_3 w_2) \ihat + (v_3 w_1 - v_1 w_3) \jhat + (v_1 w_2 - v_2 w_1) \khat = \left|\matrix{ \ihat & \jhat & \khat \cr v_1 & v_2 & v_3 \cr w_1 & w_2 & w_3 \cr}\right|.$

Strictly speaking, you should take the first equality as the definition and the second equality as a helpful way to remember how to compute it. Why?

Determinants are defined for matrices all of whose entries are numbers. In more advanced courses, you may see that "numbers" can in general be elements in an algebraic structure called a commutative ring with identity. The problem with the determinant above is that the elements of the first row are vectors, while the other elements are numbers. It is not clear what single algebraic structure contains the elements of the matrix, or if the properties of determinants which hold for numerical matrices will hold for matrices like the one above.

We will see this casual use of determinants in other places --- for example, when we discuss the curl of a vector field. Fortunately, with a little care in using these shortcuts everything works as you'd expect.

Example. Compute $(1, 3, -5) \times (2, 2, -3)$ .

$(1, 3, -5) \times (2, 2, -3) = \left|\matrix{\ihat & \jhat & \khat \cr 1 & 3 & -5 \cr 2 & 2 & -3 \cr}\right| = (1, -7, -4).\quad\halmos$

Here are some algebraic properties of the cross product.

Proposition. Let $\vec{a} = (a_1, a_2, a_3)$ , $\vec{b} = (b_1, b_2, b_3)$ , and $\vec{c} = (c_1, c_2, c_3)$ be 3-dimensional vectors and let k be a number.

(a) $\vec{a} \times (\vec{b} + \vec{c}) = \vec{a} \times \vec{b} + \vec{a} \times \vec{c}$ .

(b) $\vec{a} \times \vec{a} = \vec{0}$ .

(d) $(k \vec{a}) \times \vec{b} = \vec{a} \times (k \vec{b}) = k(\vec{a} \times \vec{b})$ .

(e) (Triple scalar product)

$(\vec{a} \times \vec{b}) \cdot \vec{c} = \vec{a} \cdot (\vec{b} \times \vec{c}) = \left|\matrix{ a_1 & a_2 & a_3 \cr b_1 & b_2 & b_3 \cr c_1 & c_2 & c_3 \cr}\right|.$

(f) $\vec{a} \times \vec{b}$ is orthogonal to $\vec{a}$ and to $\vec{b}$ .

Proof. The idea in each case is to write the vectors in terms of components, then compute.

For example, here's the proof of (a):

$\vec{a} \times (\vec{b} + \vec{c}) = (a_1, a_2, a_3) \times ((b_1, b_2, b_3) + (c_1, c_2, c_3)) = (a_1, a_2, a_3) \times (b_1 + c_1, b_2 + c_2, b_3 + c_3) =$

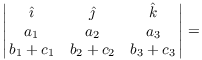
$\left|\matrix{ \ihat & \jhat & \khat \cr a_1 & a_2 & a_3 \cr b_1 + c_1 & b_2 + c_2 & b_3 + c_3 \cr}\right| =$

$\left(a_2 (b_3 + c_3) - a_3 (b_2 + c_2)\right)\ihat + \left(a_3 (b_1 + c_1) - a_1 (b_3 + c_3)\right)\jhat + \left(a_1 (b_2 + c_2) - a_2 (b_1 + c_1)\right)\khat =$

$\left(a_2 b_3 + a_2 c_3 - a_3 b_2 - a_3 c_2\right)\ihat + \left(a_3 b_1 + a_3 c_1 - a_1 b_3 - a_1 c_3\right)\jhat + \left(a_1 b_2 + a_1 c_2 - a_2 b_1 - a_2 c_1\right)\khat =$

$\left(a_2 b_3 - a_3 b_2\right)\ihat + \left(a_3 b_1 - a_1 b_3\right)\jhat + \left(a_1 b_2 - a_2 b_1)\right)\khat + \left(a_2 c_3 - a_3 c_2\right)\ihat + \left(a_3 c_1 - a_1 c_3\right)\jhat + \left(a_1 c_2 - a_2 c_1)\right)\khat =$

$\left|\matrix{ \ihat & \jhat & \khat \cr a_1 & a_2 & a_3 \cr b_1 & b_2 & b_3 \cr}\right| + \left|\matrix{ \ihat & \jhat & \khat \cr a_1 & a_2 & a_3 \cr c_1 & c_2 & c_3 \cr}\right| = \vec{a} \times \vec{b} + \vec{a} \times \vec{c}.$

For (e), I have

$\left|\matrix{ a_1 & a_2 & a_3 \cr b_1 & b_2 & b_3 \cr c_1 & c_2 & c_3 \cr}\right| = a_1 (b_2 c_3 - b_3 c_2) - a_2 (b_3 c_1 - b_1 c_3) + a_3 (b_1 c_2 - b_2 c_1) =$

$a_1 \left|\matrix{b_2 & b_3 \cr c_2 & c_3 \cr}\right| - a_2 \left|\matrix{b_1 & b_3 \cr c_1 & c_3 \cr}\right| + a_3 \left|\matrix{b_1 & b_2 \cr c_1 & c_2 \cr}\right| = (a_1, a_2, a_3) \cdot \left(\left|\matrix{b_2 & b_3 \cr c_2 & c_3 \cr}\right| \ihat - \left|\matrix{b_1 & b_3 \cr c_1 & c_3 \cr}\right| \jhat + \left|\matrix{b_1 & b_2 \cr c_1 & c_2 \cr}\right| \khat\right) =$

$(a_1, a_2, a_3) \cdot \left|\matrix{ \ihat & \jhat & \khat \cr b_1 & b_2 & b_3 \cr c_1 & c_2 & c_3 \cr}\right| = \vec{a} \cdot (\vec{b} \times \vec{c}).$

Then using this formula with $\vec{a}$ replaced with $\vec{c}$ , $\vec{b}$ replaced with $\vec{a}$ , and $\vec{c}$ replaced with $\vec{b}$ , I have

$(\vec{a} \times \vec{b}) \cdot \vec{c} = \vec{c} \cdot (\vec{a} \times \vec{b}) = \left|\matrix{ c_1 & c_2 & c_3 \cr a_1 & a_2 & a_3 \cr b_1 & b_2 & b_3 \cr}\right| = -\left|\matrix{ b_1 & b_2 & b_3 \cr a_1 & a_2 & a_3 \cr c_1 & c_2 & c_3 \cr}\right| = \left|\matrix{ a_1 & a_2 & a_3 \cr b_1 & b_2 & b_3 \cr c_1 & c_2 & c_3 \cr}\right| = \vec{a} \cdot (\vec{b} \times \vec{c}).$

The third and fourth equalities used the fact that swapping two rows multiplies a determinant by -1.

Now it's easy to prove (f). Since the determinant of a matrix with two equal rows is 0,

$\vec{a} \cdot (\vec{a} \times \vec{b}) = \left|\matrix{ a_1 & a_2 & a_3 \cr a_1 & a_2 & a_3 \cr b_1 & b_2 & b_3 \cr}\right| = 0.$

This proves that $\vec{a}$ is perpendicular to $\vec{a} \times \vec{b}$ . A similar argument proves the result for $\vec{b}$ .

I'll show below that $\vec{a} \cdot (\vec{b} \times \vec{c})$ has a geometric interpretation: Its absolute value is the volume of the parallelepiped determined by $\vec{a}$ , $\vec{b}$ , and $\vec{c}$ .

Property (c) shows that the cross product is not commutative. In fact, it is also not associative: In general, $(\vec{a} \times \vec{b}) \times \vec{c} \ne \vec{a} \times (\vec{b} \times \vec{c})$ .

Example. Show that

$[(1, 2, 0) \times (-1, 1, 1)] \times (2, 1, 1) \ne (1, 2, 0) \times [(-1, 1, 1) \times (2, 1, 1)].$

$(1, 2, 0) \times (-1, 1, 1) = \left|\matrix{ \ihat & \jhat & \khat \cr 1 & 2 & 0 \cr -1 & 1 & 1 \cr}\right| = (2, -1, 3).$

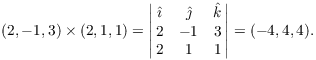
$(2, -1, 3) \times (2, 1, 1) = \left|\matrix{ \ihat & \jhat & \khat \cr 2 & -1 & 3 \cr 2 & 1 & 1 \cr}\right| = (-4, 4, 4).$

Thus,

$[(1, 2, 0) \times (-1, 1, 1)] \times (2, 1, 1) = (-4, 4, 4).$

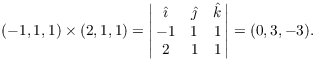
$(-1, 1, 1) \times (2, 1, 1) = \left|\matrix{ \ihat & \jhat & \khat \cr -1 & 1 & 1 \cr 2 & 1 & 1 \cr}\right| = (0, 3, -3).$

$(1, 2, 0) \times (0, 3, -3) = \left|\matrix{ \ihat & \jhat & \khat \cr 1 & 2 & 0 \cr 0 & 3 & -3 \cr}\right| = (-6, 3, 3).$

Thus,

$(1, 2, 0) \times [(-1, 1, 1) \times (2, 1, 1)] = (-6, 3, 3).$

Hence,

$[(1, 2, 0) \times (-1, 1, 1)] \times (2, 1, 1) \ne (1, 2, 0) \times [(-1, 1, 1) \times (2, 1, 1)].\quad\halmos$

The next result gives part of the geometric interpretation of the cross product. It's routine --- just writing vectors out in terms of components and computing --- but pretty technical. You might want to skip the proof and try to understand the statement.

Proposition. Let $\vec{a}$ and $\vec{b}$ be 3-dimensional vectors. Then

$\|\vec{a} \times \vec{b}\| = \|\vec{a}\| \|\vec{b}\| \sin \theta.$

$\theta$ is the angle from $\vec{a}$ to $\vec{b}$ satisfying $0 \le \theta \le \pi$ .

Proof. First, note that

$(\vec{a} \cdot \vec{b})^2 = (a_1 b_1 + a_2 b_2 + a_3 b_3)^2 = (a_1^2 b_1^2 + a_2^2 b_2^2 + a_3^2 b_3^2) + (2 a_1 a_2 b_1 b_2 + 2 a_1 a_3 a_1 b_3 + 2 a_2 a_3 b_2 b_3).$

$2 a_1 a_2 b_1 b_2 + 2 a_1 a_3 a_1 b_3 + 2 a_2 a_3 b_2 b_3 = (\vec{a} \cdot \vec{b})^2 - (a_1^2 b_1^2 + a_2^2 b_2^2 + a_3^2 b_3^2).$

I'll use the last result in the middle of the following computation:

$\|\vec{a} \times \vec{b}\|^2 = (\vec{a} \times \vec{b}) \cdot (\vec{a} \times \vec{b}) = (a_2 b_3 - a_3 b_2, a_3 b_1 - a_1 b_3, a_1 b_2 - a_2 b_1) \cdot (a_2 b_3 - a_3 b_2, a_3 b_1 - a_1 b_3, a_1 b_2 - a_2 b_1) =$

$(a_2^2 b_3^2 + a_3^2 b_2^2 + a_3^2 b_1^2 + a_1^2 b_3^2 + a_1^2 b_2^2 + a_2^2 b_1^2) - [(\vec{a} \cdot \vec{b})^2 - (a_1^2 b_1^2 + a_2^2 b_2^2 + a_3^2 b_3^2)] =$

$(a_1^2 b_1^2 + a_2^2 b_2^2 + a_3^2 b_3^2 + a_2^2 b_3^2 + a_3^2 b_2^2 + a_3^2 b_1^2 + a_1^2 b_3^2 + a_1^2 b_2^2 + a_2^2 b_1^2) - (\vec{a} \cdot \vec{b})^2 =$

$(a_1^2 + a_2^2 + a_3^2)(b_1^2 + b_2^2 + b_3^2) - (\vec{a} \cdot \vec{b})^2 = \|\vec{a}\|^2 \|\vec{b}\|^2 - (\|\vec{a}\| \|\vec{b}\| \cos \theta)^2 = \|\vec{a}\|^2 \|\vec{b}\|^2 [1 - (\cos \theta)^2] = \|\vec{a}\|^2 \|\vec{b}\|^2 (\sin \theta)^2.$

Taking the square root on both sides, and noting that $0 \le \theta \le \pi$ implies that $\sin \theta \ge 0$ , I have

$\|\vec{a} \times \vec{b}\| = \|\vec{a}\| \|\vec{b}\| \sin \theta.\quad\halmos$

So far, I know that $\vec{a} \times \vec{b}$ is a vector which is perpendicular to both $\vec{a}$ and $\vec{b}$ , and whose length is $\|\vec{a}\| \|\vec{b}\| \sin \theta$ . This almost determines $\vec{a} \times \vec{b}$ ; the only question is which of the two possible perpendicular vectors it could be:

$\hbox{\epsfysize=1.5in \epsffile{cross-product-1.eps}}$

In this picture, $\vec{a} \times \vec{b}$ turns out to be the perpendicular vector pointing "upward"; the one pointing "downward" is actually $\vec{b} \times \vec{a} = -(\vec{a} \times \vec{b})$ .

Definition. An ordered set of vectors $(\vec{a}, \vec{b}, \vec{c})$ in $\real^3$ is positively oriented (or has a right-hand orientation) if

$\det \left[\matrix{ \leftarrow \vec{a} \rightarrow \cr \leftarrow \vec{b} \rightarrow \cr \leftarrow \vec{c} \rightarrow \cr}\right] > 0.$

(That is, make a matrix with the vectors in the given order as its rows and take the determinant.)

If the determinant is negative, the ordered set of vectors is negatively oriented (or has a left-hand orientation).

"Ordered set" means that if you keep the three vectors the same but change the order in which they're listed, you have a different ordered set.

Example. Show that the ordered set $(\ihat, \jhat, \khat)$ is positively oriented.

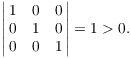
$\left|\matrix{ 1 & 0 & 0 \cr 0 & 1 & 0 \cr 0 & 0 & 1 \cr}\right| = 1 > 0.$

Hence, the set is positively oriented.

Proposition. If $\vec{a}$ and $\vec{b}$ are nonzero and nonparallel, then $\vec{a} \times \vec{b}$ is a vector whose length is $\|\vec{a}\| \|\vec{b}\| \sin \theta$ , and whose direction is perpendicular to $\vec{a}$ and $\vec{b}$ , so that $(\vec{a}, \vec{b}, \vec{a} \times \vec{b})$ is positively oriented.

In other words, it is like the convention with the positive x, y, and z-axes in $\real^3$ : If you curl the fingers of your right hand through the smaller angle from $\vec{a}$ to $\vec{b}$ , your thumb points in the direction of $\vec{a} \times \vec{b}$ .

Proof. Using the triple scalar product,

$\det \left[\matrix{ \leftarrow \vec{a} \rightarrow \cr \leftarrow \vec{b} \rightarrow \cr \leftarrow \vec{a} \times \vec{b} \rightarrow \cr}\right] = \vec{a} \cdot [\vec{b} \times (\vec{a} \times \vec{b})] = (\vec{a} \times \vec{b}) \cdot (\vec{a} \times \vec{b}) = \|\vec{a} \times \vec{b}\|^2 \ge 0.$

Now $\|\vec{a} \times \vec{b}\| = \|\vec{a}\| \|\vec{b}\| \sin \theta$ . Since $\vec{a}$ and $\vec{b}$ are nonzero, $\|\vec{a}\|$ and $\|\vec{b}\|$ are nonzero. Since Since $\vec{a}$ and $\vec{b}$ aren't parallel, $\sin \theta \ne 0$ .

Therefore, $\|\vec{a} \times \vec{b}\|^2 > 0$ .

This shows that the set $(\vec{a}, \vec{b}, \vec{a} \times \vec{b})$ is positively oriented. The other assertions have been proven above.

Example. Find two unit vectors perpendicular to both and .

$(3, -1, 1) \times (6, 1, 4) = \left|\matrix{ \ihat & \jhat & \khat \cr 3 & -1 & 1 \cr 6 & 1 & 4 \cr}\right| = (-5, -6, 9).$

Now

$\|(-5, -6, 9)\| = \sqrt{25 + 36 + 81} = \sqrt{142}.$

So the two unit vectors perpendicular to both and are $\pm \dfrac{1}{\sqrt{142}} (-5, -6, 9)$ .

Geometrically, the length of $\vec{a} \times \vec{b}$ is the area of the parallelogram determined by $\vec{a}$ and $\vec{b}$ .

$\hbox{\epsfysize=1.25in \epsffile{cross-product-2.eps}}$

As the picture shows, $\|\vec{a}\|$ is the length of the base of the parallelogram and $\|\vec{b}\| \sin \theta$ is the altitude of the parallelogram. Consequently, their product is the area of the parallelogram, which is just

$\|\vec{a}\| \|\vec{b}\| \sin \theta = \|\vec{a} \times \vec{b}\|.$

Example. The verices of a parallelogram, listed counterclockwise, are , , , and . Find the area of the parallelogram.

$\bvec{A B} = (1, 3, -1)$ and $\bvec{A D} = (4, 1, 2)$ . Then

$\bvec{A B} \times \bvec{A D} = \left|\matrix{ \ihat & \jhat & \khat \cr 1 & 3 & -1 \cr 4 & 1 & 2 \cr}\right| = (7, -6, -11).$

The area is

$\|\bvec{A B} \times \bvec{A D}\| = \sqrt{49 + 36 + 121} = \sqrt{206}.\quad\halmos$

Example. Find the area of the parallelogram whose vertices are , , , . What is the area of $\triangle ABC$ ?

The parallelogram is pictured below:

$\hbox{\epsfysize=1.5in \epsffile{cross-product-3.eps}}$

$\bvec{A B} = (1, 1)$ and $\bvec{A C} = (2, -2)$ are adjacent sides of the parallelogram. In order to take their cross product, regard them as 3-dimensional vectors with zero z-components: $\bvec{AB} = (1, 1, 0)$ and $\bvec{AC} = (2, -2, 0)$ .

Then

$\bvec{A B} \times \bvec{A C} = \left|\matrix{ \ihat & \jhat & \khat \cr 1 & 1 & 0 \cr 2 & -2 & 0 \cr}\right| = (0, 0, -4).$

The area of the parallelogram is $\|\bvec{A B} \times \bvec{A C}\| = 4$ . The area of the triangle is half the area of the parallelogram: 2.

$\vec u \cdot (\vec v \times \vec w)$ has the following geometric interpretation: Its absolute value gives the volume of the parallelepiped determined by $\vec u$ , $\vec v$ , and $\vec w$ :