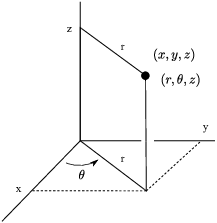
Cylindrical Coordinates

Cylindrical coordinates assigned an ordered triple $(r, \theta, z)$ to points in space. If the rectangular coordinates of the point are $(x, y, z)$ , then $(r, \theta)$ are the polar coordinates of the point $(x, y)$ ; the third coordinate z is the same in both cylindrical and rectangular.

$$\hbox{\epsfysize=2in \epsffile{cylindrical-coordinates-1.eps}}$$

Example. A point has rectangular coordinates $(-2, 2, 2\sqrt{6})$ . Find its cylindrical coordinates.

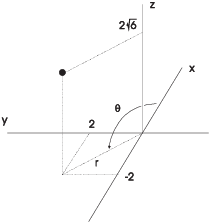
$$\hbox{\epsfysize=2 in \epsffile{cylindrical-coordinates-2.eps}}$$

Since the point lies above the second quadrant, I've rotated the coordinates axes so that the second quadrant is "in front". From the picture, it's clear that $\theta = \dfrac{\pi}{2} + \dfrac{\pi}{4} = \dfrac{3 \pi}{4}$ . By Pythagoras, $r = 2 \sqrt{2}$ .

The cylindrical coordinates are $\left(2\sqrt{2}, \dfrac{3 \pi}{4}, 2\sqrt{6}\right)$ .

Example. A point has cylindrical coordinates $\left(4,\dfrac{5 \pi}{3}, -4\right)$ . Find its rectangular coordinates.

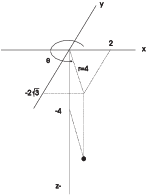
$$\hbox{\epsfysize=1.75 in \epsffile{cylindrical-coordinates-3.eps}}$$

The point lies below the fourth quadrant. Its rectangular coordinates are $(2, -2\sqrt{3}, -4)$ .

Example. Find the equation of the unit sphere $x^2 + y^2 + z^2 = 1$ in cylindrical coordinates.

Setting $x^2 + y^2 = r^2$ , I get

$$r^2 + z^2 = 1.\quad\halmos$$

Example. Convert $y = 2 x$ to cylindrical coordinates.

$$\dfrac{y}{x} = 2, \quad\hbox{so}\quad \tan \theta = 2.\quad\halmos$$

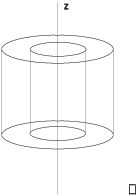
Example. What is the set of points which satisfy the cylindrical coordinate equation $r^2 - 3 r + 2 = 0$ ?

The equation is $(r - 1)(r - 2) = 0$ , so $r = 1$ or $r = 2$ . The locus consists of two concentric cylinders of radius 1 and 2 having the z-axis as their axis.

$$\hbox{\epsfysize=1.75 in \epsffile{cylindrical-coordinates-4.eps}}\quad\halmos$$

To convert a triple integral $\displaystyle \tint_R f(x, y, z)\,dx\,dy\,dz$ to cylindrical coordinates:

1. Convert $f(x, y, z)$ to cylindrical coordinates using the polar coordinate conversion equations.

2. To obtain the limits of integration, describe the region R by inequalities in cylindrical coordinates.

3. Replace $dx\,dy\,dz$ with $r\,dr\,d\theta\,dz$ .

In converting a double integral from rectangular to polar, we replace $dx\,dy$ with $r\,dr\,d\theta$ , so this is reasonable from that point of view. You can see the factor of r from the change of variables formula. The transformation is

$$x = r \cos \theta, \quad y = r \sin \theta, \quad z = z.$$

The Jacobian is

$$\det \left[\matrix{ \cos \theta & -r \sin \theta & 0 \cr \sin \theta & r \cos \theta & 0 \cr 0 & 0 1 \cr}\right] = r (\cos \theta)^2 + r (\sin \theta)^2 = r.$$

Assuming that r is positive, the change of variables formula tells us to replace $dx\,dy\,dz$ with $r\,dr\,d\theta\,dz$ .

Example. Let R be the region bounded below by $z = x^2 + y^2$ and above by $z = 36$ . Compute

$$\tint_R (x^2 + y^2 + 1)\,dx\,dy\,dz.$$

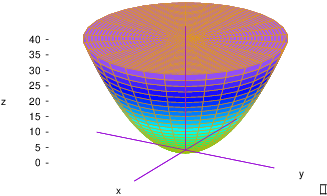
$$\hbox{\epsfysize=1.75 in \epsffile{cylindrical-coordinates-5.eps}}\quad\halmos$$

The intersection of $z = x^2 + y^2$ and $z = 36$ is $x^2 + y^2 = 36$ , a circle of radius 6 centered at the origin. Hence, the region of integration is

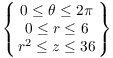
$$\left\{\matrix{ 0 \le \theta \le 2 \pi \cr 0 \le r \le 6 \cr r^2 \le z \le 36}\right\}$$

Note that $x^2 + y^2 + 1 = r^2 + 1$ . The integral is

$$\int_0^{2 \pi} \int_0^6 \int_{r^2}^{36} (r^2 + 1) \cdot r\,dz\,dr\,d\theta = 2 \pi \int_0^6 (r^3 + r) \left[z\right]_{r^2}^{36}\,dr = 2 \pi \int_0^6 (r^3 + r)(36 - r^2)\,dr =$$

$$2 \pi \int_0^6 (36 r + 35 r^3 - r^5)\,dr = 2 \pi \left[18 r^2 + \dfrac{35}{4} r^4 - \dfrac{1}{6} r^6\right]_0^6 = 8424 \pi = 26464.77651 \ldots.\quad\halmos$$

Contact information

Bruce Ikenaga's Home Page

Copyright 2018 by Bruce Ikenaga