The Dot Product

If $\vec{v} = (v_1, v_2, v_3)$ and $\vec{w} = (w_1, w_2, w_3)$ are vectors, the dot product of $\vec{v}$ and $\vec{w}$ is defined algebraically as

$$\vec{v} \cdot \vec{w} = v_1 w_1 + v_2 w_2 + v_3 w_3.$$

Example. (a) Compute the dot product $(2, 3, -7) \cdot (-3, 2, 0)$ .

(b) Compute the dot product $(4 \ihat - \jhat + 7 \khat) \cdot (-2 \ihat - 3 \jhat + 11 \khat)$ .

(a)

$$(2, 3, -7) \cdot (-3, 2, 0) = (2)(-3) + (3)(2) + (-7)(0) = 0.$$

(b)

$$(4 \ihat - \jhat + 7 \khat) \cdot (-2 \ihat - 3 \jhat + 11 \khat) = (4)(-2) + (-1)(-3) + (7)(11) = 72.\quad\halmos$$

The dot product of two vectors is a number. Since numbers are often referred to as scalars, the dot product is often called the scalar product.

The definition works just as well for vectors with 2 components, or more than 3 components. For example, here is the dot product of two 4-dimensional vectors:

$$(3, -4, -1, -1) \cdot (0, 2, -2, 5) = (3)(0) + (-4)(2) + (-1)(-2) + (-1)(5) = -11.$$

Here are some properties of the dot product.

Theorem. Let $k \in \real$ and let $\vec{u}, \vec{v}, \vec{w} \in \real^n$ .

(a) $\vec{v} \cdot \vec{w} = \vec{w} \cdot \vec{v}$

(b) $\vec{u} \cdot (\vec{v} + \vec{w}) = \vec{u} \cdot \vec{v} + \vec{u} \cdot \vec{w}$

(c) $k (\vec{v} \cdot \vec{w}) = (k \vec{v}) \cdot \vec{w} = \vec{v} \cdot (k \vec{w})$

(d) $\vec{v} \cdot \vec{v} = \|\vec{v}\|^2$

Proof. All of these results can be proved by writing the vectors in terms of components and computing.

As an example, I'll prove (d) for 3-dimensional vectors. Suppose $\vec{v} = (v_1, v_2, v_3)$ . Then

$$\vec{v} \cdot \vec{v} = v_1^2 + v_2^2 + v_3^2 = \|\vec{v}\|^2.\quad\halmos$$

The dot product also has a geometric interpretation.

Theorem. Let $\vec{v}$ and $\vec{w}$ be vectors and let $\theta$ be the angle between them. Then

$$\vec{v} \cdot \vec{w} = \|\vec{v}\| \|\vec{w}\| \cos \theta.$$

Note: Since $\cos \theta = \cos (-\theta)$ , it does not matter whether $\theta$ is measured counterclockwise or clockwise.

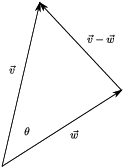
$$\hbox{\epsfysize=1.5in \epsffile{dot-product-1.eps}}$$

Proof. Apply the Law of Cosines and use the fact that $\vec{a} \cdot \vec{a} = \|\vec{a}\|^2$ :

$$\eqalign{ \|\vec{v} - \vec{w}\|^2 & = \|\vec{v}\|^2 + \|\vec{w}\|^2 - 2 \|\vec{v}\| \|\vec{w}\| \cos \theta \cr (\vec{v} - \vec{w}) \cdot (\vec{v} - \vec{w}) & = \|\vec{v}\|^2 + \|\vec{w}\|^2 - 2 \|\vec{v}\| \|\vec{w}\| \cos \theta \cr \vec{v} \cdot \vec{v} - 2 \vec{v} \cdot \vec{w} + \vec{w} \cdot \vec{w} & = \|\vec{v}\|^2 + \|\vec{w}\|^2 - 2 \|\vec{v}\| \|\vec{w}\| \cos \theta \cr \|\vec{v}\|^2 - 2 \vec{v} \cdot \vec{w} + \|\vec{w}\|^2 & = \|\vec{v}\|^2 + \|\vec{w}\|^2 - 2 \|\vec{v}\| \|\vec{w}\| \cos \theta \cr -2 \vec{v} \cdot \vec{w} & = -2 \|\vec{v}\| \|\vec{w}\| \cos \theta \cr \vec{v} \cdot \vec{w} & = \|\vec{v}\| \|\vec{w}\| \cos \theta \cr} \quad\halmos$$

You can often use vectors to obtain results by computing things algebraically, then interpreting the results geometrically. In this case, you can do this because there are two ways of looking at the dot product.

For example, when will two vectors be perpendicular? This will happen if the angle between them is $\theta = \pm \dfrac{\pi}{2}$ . In either case, $\cos \theta = 0$ , and hence $\vec{v} \cdot \vec{w} = 0$ .

Going the other way, if $\vec{v}$ and $\vec{w}$ are nonzero vectors and $\vec{v} \cdot \vec{w} = 0$ , then $|\vec{v}||\vec{w}| \cos \theta = 0$ . Therefore, $\cos \theta = 0$ , so $\theta = \pm \dfrac{\pi}{2}$ and the vectors are perpendicular.

Notes. 1. The word " orthogonal" is synonymous with "perpendicular".

2. The zero vector $\vec{0}$ is trivially perpendicular to any other vector. But usually you want a nonzero vector perpendicular to another vector, and I'll try to be careful to ask for a nonzero vector.

In addition:

(a) If $\cos \theta > 0$ , the angle between the vectors is acute.

(b) If $\cos \theta < 0$ , the angle between the vectors is obtuse.

Note that you can prove these geometric facts about two vectors even though it might be hard to determine them by drawing the vectors. And while we'll be primarily concerned with vectors in 2 and 3 dimensions, these facts about angles and dot products are true in n dimensions.

Example. Determine whether the vectors make an acute angle, an obtuse angle, or are perpendicular.

(a) $\vec{v} = (1, -5, 6)$ , $\vec{w} = (2, 2, -7)$ .

(b) $\vec{v} = (2, 1, -2, 2)$ , $\vec{w} = (4, 0, -3, -7)$

(a)

$$\vec{v} \cdot \vec{w} = 2 - 10 - 42 = -50.$$

Since $\vec{v} \cdot \vec{w} < 0$ , $\cos \theta < 0$ , and the angle between the vectors is obtuse.

$$\vec{v} \cdot \vec{w} = 8 + 0 + 6 - 14 = 0.$$

The vectors are perpendicular.

Example. Find the exact value of the cosine of the angle between $(3, -2, 1)$ and $(-2, 5, 3)$ .

Tell whether the vectors are orthogonal; if not, tell whether the angle between them is acute or obtuse.

$$\cos \theta = \dfrac{(3, -2, 1) \cdot (-2, 5, 3)}{\|(3, -2, 1)\| \|(-2, 5, 3)\|} = \dfrac{-6 - 10 + 3}{\sqrt{14} \sqrt{38}} = \dfrac{-13}{\sqrt{532}}.$$

The angle is obtuse.

Example. Find two unit vectors which are perpendicular to $(2, 5)$ . How many unit vectors are perpendicular to $(1, -3, 3)$ ?

$(5, -2)$ is perpendicular to $(2, 5)$ , since the two vectors have dot product 0 by inspection. $\|(5, -2)\| = \sqrt{29}$ , so the vectors $\dfrac{1}{29}(5, -2)$ and $-\dfrac{1}{29}(5, -2)$ are unit vectors perpendicular to $(2, 5)$ .

There are infinitely many unit vectors perpendicular to $(1, -3, 3)$ .

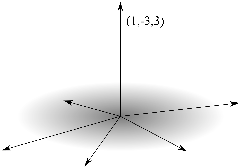
$$\hbox{\epsfysize=1.5in \epsffile{dot-product-2.eps}}$$

If $(1, -3, 3)$ is like a flagpole, think of vectors pointing along the ground away from the base of the flagpole. Each may be divided by its length to get a unit vector.

Algebraically, they are the unit vectors $(a, b, c)$ such that $a - 3 b + 3 c = 0$ .

Example. Find a nonzero vector which is simultaneously orthogonal to both $(1, 3, 2)$ and $(2, 5, -4)$ .

Let $(a, b, c)$ be such a vector. I want

$$(1, 3, 2) \cdot (a, b, c) = 0 \quad\hbox{and}\quad (2, 5, -4) \cdot (a, b, c) = 0.$$

This gives the equations

$$a + 3 b + 2 c = 0 \quad\hbox{and}\quad 2 a + 5 b - 4 c = 0.$$

Since I have two equations but three variables, I can't expect a unique solution.

I'll eliminate one of the variables to start with. The first equation gives

$$a = -3 b - 2 c.$$

Substitute this into $2 a + 5 b - 4 c = 0$ to get

$$2(-3 b - 2 c) + 5 b - 4 c = 0, \quad\hbox{or}\quad -b - 8 c = 0.$$

At this point, I can assign a value of my choice to one of the variables. Let $c = 1$ . Then $-b - 8 = 0$ , so $b = -8$ . Plugging these values into $a = -3 b - 2 c$ , I get $a = 24 - 2 = 22$ .

Thus, $(22, -8, 1)$ is perpendicular to $(1, 3, 2)$ and $(2, 5, -4)$ . In fact, any solution must be a multiple of the vector I found, since the vectors perpendicular to both $(1, 3, 2)$ and $(2, 5, -4)$ form a line.

$$\hbox{\epsfysize=2in \epsffile{dot-product-6.eps}}\quad\halmos$$

Example. Find vectors $\vec{u}$ , $\vec{v}$ , and $\vec{w}$ such that

$$\vec{u} \cdot \vec{v} = \vec{u} \cdot \vec{w} \quad\hbox{but}\quad \vec{v} \ne \vec{w}.$$

There are lots of possibilities. For instance,

$$(2, 4) \cdot (-2, 1) = 0 = (2, 4) \cdot (-6, 3).$$

But $(-2, 1) \ne (-6, 3)$ .

The scalar component of $\vec{v}$ in the direction of $\vec{w}$ is

$$\comp_{\vec{w}}\vec{v} = \dfrac{\vec{v} \cdot \vec{w}}{\|\vec{w}\|}.$$

It gives the (signed) length of the "shadow" that $\vec{v}$ makes on $\vec{w}$ . It is positive if $\vec{v}$ and $\vec{w}$ point in the same direction (i.e. if the angle between them is acute) and negative if $\vec{v}$ and $\vec{w}$ point in the opposite direction (i.e. if the angle between them is obtuse).

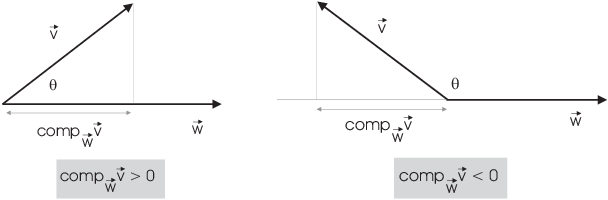
$$\hbox{\epsfxsize=2in \epsffile{dot-product-3a.eps}} \hskip0.5in \hbox{\epsfxsize=3in \epsffile{dot-product-3b.eps}}$$

To see this, consider the right triangle in the picture. The base of the triangle is $\comp_{\vec{w}}\vec{v}$ , and

$$\dfrac{(\hbox{base})}{\|\vec{v}\|} = \cos \theta, \quad\hbox{so}\quad (\hbox{base}) = \|\vec{v}\|\cos \theta.$$

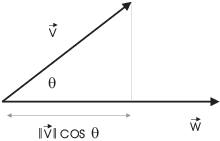
$$\hbox{\epsfysize=1.25in \epsffile{dot-product-4.eps}}$$

But

$$\cos \theta = \dfrac{\vec{v}\cdot \vec{w}}{\|\vec{v}\|\|\vec{w}\|}, \quad\hbox{so}\quad \|\vec{v}\|\cos \theta = \dfrac{\vec{v} \cdot \vec{w}}{\|\vec{w}\|}.$$

Therefore,

$$(\hbox{base}) = \dfrac{\vec{v} \cdot \vec{w}}{\|\vec{w}\|}, \quad\hbox{so}\quad \comp_{\vec{w}}\vec{v} = \dfrac{\vec{v} \cdot \vec{w}}{\|\vec{w}\|}.$$

Example. If $\vec{v} = (1, 4, -5)$ and $\vec{w} = (2, 1, -2)$ , find the scalar component of $\vec{v}$ in the direction of $\vec{w}$ .

$$\comp_{\vec{w}}\vec{v} = \dfrac{(1, 4, -5) \cdot (2, 1, -2)}{\|(2, 1, -2)\|} = \dfrac{16}{3}.\quad\halmos$$

The vector projection of $\vec{v}$ in the direction of $\vec{w}$ is vector whose (signed) length is $\comp_{\vec{w}} \vec{v}$ and whose direction is the direction of $\vec{w}$ .

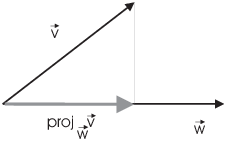
$$\hbox{\epsfysize=1.25in \epsffile{dot-product-5.eps}}$$

To obtain it, I multiply $\comp_{\vec{w}} \vec{v}$ by the unit vector $\dfrac{\vec{w}}{\|\vec{w}\|}$ which has the same direction as $\vec{w}$ . This gives

$$\proj_{\vec{w}}\vec{v} = (\comp_{\vec{w}} \vec{v})\left(\dfrac{\vec{w}}{\|\vec{w}\|}\right) = \left(\dfrac{\vec{v} \cdot \vec{w}}{|\vec{w}|}\right) \left(\dfrac{\vec{w}}{\|\vec{w}\|}\right) = \dfrac{\vec{v} \cdot \vec{w}}{|\vec{w}|^2}\vec{w} = \dfrac{\vec{v} \cdot \vec{w}}{\vec{w}\cdot \vec{w}}\vec{w}.$$

Thus, the formula is

$$\proj_{\vec{w}}\vec{v} = \dfrac{\vec{v} \cdot \vec{w}}{\vec{w} \cdot \vec{w}}\vec{w}.$$

Example. Find the vector projection of $\vec{v} = 2 \ihat - \jhat + \khat$ in the direction of $\vec{w} = 4 \ihat + 3 \khat$ .

$$\proj_{\vec{w}} \vec{v} = \dfrac{(2,-1, 1) \cdot (4, 0, 3)}{(4, 0, 3) \cdot (4, 0, 3)} (4, 0, 3) = \dfrac{11}{25}(4, 0, 3) = \dfrac{44}{25} \ihat + \dfrac{33}{25} \khat.\quad\halmos$$

Contact information

Bruce Ikenaga's Home Page

Copyright 2017 by Bruce Ikenaga