Double Integrals in Polar

It's often useful to change variables and convert a double integral from rectangular coordinates to polar coordinates. Suppose you're trying to convert the following integral to polar coordinates:

$$\dint_D f(x,y)\,dx\,dy.$$

1. Convert the function $f(x,y)$ to polar by using the polar-rectangular conversion equations:

$$r^2 = x^2 + y^2, \quad \tan \theta = \dfrac{y}{x},$$

$$x = r\cos \theta, \quad y = r\sin \theta.$$

2. Replace $dx\,dy$ with $r\,dr\,d\theta$ .

3. Describe the region of integration D by inequalities in polar and use the inequalities to change the limits.

The only thing which requires explanation is why you replace $dx\,dy$ with $r\,dr\,d\theta$ . One way to understand this is to use the change-of-variables formula for double integrals. This says that

$$dx\,dy = \left|\matrix{ \pder x r & \pder x \theta \cr \pder y r & \pder y \theta \cr}\right|\,dr\,d\theta = \left|\matrix{ \cos \theta & -r\sin \theta \cr \sin \theta & r\cos \theta \cr}\right|\,dr\,d\theta = \left[r(\cos \theta)^2 + r(\sin \theta)^2\right]\,dr\,d\theta = r\,dr\,d\theta.$$

Heuristically, you can picture this by considering a small wedge of area in the polar grad:

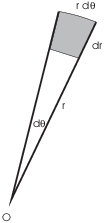
$$\hbox{\epsfysize=2 in \epsffile{double-integrals-in-polar-1.eps}}$$

The "box" has height $dr$ and width $r\,d\theta$ --- the width coming from the formula for an arc of radius r subtended by an angle $d\theta$ . The area of the box should be $r\,dr\,d\theta$ .

Example. Convert $\displaystyle \int_{-1}^1 \int_{-\sqrt{1 - x^2}}^{\sqrt{1 - x^2}} \dfrac{1}{(x^2 + y^2 + 1)^{3/2}}\,dx\,dy$ to polar and compute the integral.

This integral would be horrible to compute in rectangular coordinates. In polar, it's pretty easy.

First, convert the function:

$$\dfrac{1}{(x^2 + y^2 + 1)^{3/2}} = \dfrac{1}{(r^2 + 1)^{3/2}}.$$

I'll replace $dx\,dy$ with $r\,dr\,d\theta$ when I set up the integral.

To convert the limits, pull the original limits off as inequalities:

$$\left\{\matrix{ -1 \le x \le 1 \cr -\sqrt{1 - x^2} \le y \le \sqrt{1 - x^2} \cr}\right\}$$

Draw the region described by the inequalities. It is the interior of the circle $x^2 + y^2 = 1$ :

$$\hbox{\epsfysize=2 in \epsffile{double-integrals-in-polar-2.eps}}$$

Describe the region by inequalities in polar:

$$\left\{\matrix{ 0 \le \theta \le 2 \pi \cr 0 \le r \le 1 \cr}\right\}$$

Put the inequalities on the integral and compute:

$$\int_{-1}^1 \int_{-\sqrt{1 - x^2}}^{\sqrt{1 - x^2}} \dfrac{1}{(x^2 + y^2 + 1)^{3/2}}\,dx\,dy = \int_0^{2 \pi} \int_0^1 \dfrac{1}{(r^2 + 1)^{3/2}} \cdot r\,dr\,d\theta = \int_0^{2 \pi} \left[-\dfrac{1}{\sqrt{r^2 + 1}}\right]_0^1\,d\theta =$$

$$\int_0^{2 \pi} \dfrac{1}{2}\,d\theta = \left[\dfrac{1}{2}\theta\right]_0^{2 \pi} = \pi.$$

(I did $\displaystyle \int \dfrac{r\,dr}{(r^2 + 1)^{3/2}}$ by using the substitution $u = r^2 + 1$ .)

Here is a rule of thumb that was evident in the last problem:

\boxedtext{2}{Think about converting to polar when the double integral contains terms of the form $x^2 + y^2$ .}

You can use double integrals in polar to compute areas of regions in the x-y-plane. Just as with x-y double integrals,

$$\dint_D r\,dr\,d\theta \quad\hbox{gives the area of D}.$$

However, you can often use a single integral to compute the area --- the double integral is superfluous. For this reason, the next example isn't particularly practical; it just illustrates the idea.

Example. Use a double integral to compute the area of the region inside the cardioid $r = 1 + \sin \theta$ .

$$\hbox{\epsfysize=1.75 in \epsffile{double-integrals-in-polar-3.eps}}$$

I know the cardioid is traced out once as $\theta$ goes from 0 to $2 \pi$ , so the region inside is described by the inequalities

$$\left\{\matrix{ 0 \le \theta \le 2 \pi \cr 0 \le r \le 1 + \sin \theta \cr}\right\}$$

The area is given by the double integral

$$\int_0^{2 \pi} \int_0^{1 + \sin \theta} r\,dr\,d\theta = \int_0^{2 \pi} \left[\dfrac{1}{2} r^2\right]_0^{1 + \sin \theta} \,d\theta = \int_0^{2 \pi} \dfrac{1}{2} (1 + \sin \theta)^2\,d\theta = \left[\dfrac{3}{2} \theta - 2\cos \theta - \dfrac{1}{4} \sin 2 \theta\right]_0^{2 \pi} = 3 \pi.$$

(I did the $\theta$ integral by multiplying $(1 + \sin \theta)^2$ out, then applying the double angle formula to $(\sin \theta)^2$ .)

Do you notice what happened in the third step? I got the same integral $\displaystyle \int_0^{2 \pi} \dfrac{1}{2}(1 + \sin \theta)^2\,d\theta$ that I would have gotten using the old single-variable formula

$$\int_a^b \dfrac{1}{2} r^2\,d\theta.$$

It wasn't necessary to use a double integral to find this area.

Example. Compute $\displaystyle \int_{-\infty}^\infty e^{-x^2}\,dx$ .

This single variable integral is important in probability. Here's the trick to computing it: Let

$$I = \int_{-\infty}^\infty e^{-x^2}\,dx.$$

The variable in a definite integral is a dummy variable --- the value of the integral isn't changed if I change the letter. So

$$I = \int_{-\infty}^\infty e^{-y^2}\,dy.$$

Multiply the two equations:

$$I^2 = \int_{-\infty}^\infty \int_{-\infty}^\infty e^{-(x^2 + y^2)}\,dx\,dy.$$

Convert to polar: $e^{-(x^2 + y^2)} = e^{-r^2}$ , and $dx\,dy$ will be replaced with $r\,dr\,d\theta$ . The region is

$$\left\{\matrix{ -\infty < x < +\infty \cr -\infty < y < +\infty \cr}\right\}$$

This is the whole x-y plane! In polar, this is

$$\left\{\matrix{ 0 \le \theta \le 2 \pi \cr 0 \le r < +\infty \cr}\right\}$$

So

$$I^2 = \int_{-\infty}^\infty \int_{-\infty}^\infty e^{-(x^2 + y^2)}\,dx\,dy = \int_0^{2 \pi} \int_0^\infty e^{-r^2} \cdot r\,dr\,d\theta = \int_0^{2 \pi} \left(\lim_{c \to \infty} \int_0^c r e^{-r^2}\,dr\right)\,d\theta =$$

$$\int_0^{2 \pi} \left(\lim_{c \to \infty} \left[-\dfrac{1}{2} e^{-r^2}\right]_0^c\right)\,d\theta = \dfrac{1}{2} \int_0^{2 \pi} \left(\lim_{c \to \infty} (1 - e^{-c^2})\right)\,d\theta = \dfrac{1}{2} \int_0^{2 \pi} d\theta = \pi.$$

(I did $\int r e^{-r^2}\,dr$ using the substitution $u = -r^2$ .)

Therefore, $I = \sqrt{\pi}$ --- that is,

$$\int_{-\infty}^\infty e^{-x^2}\,dx = \sqrt{\pi}.\quad\halmos$$

Example. Compute the integral by converting to polar coordinates:

$$\int_0^2 \int_0^{\sqrt{2 x-x^2}} \sqrt{x^2 + y^2}\,dx\,dy$$

$\sqrt{x^2 + y^2} = \sqrt{r^2} = r$ , and I'll replace $dx\,dy$ with $r\,dr\,d\theta$ .

Pull off the limits of integration:

$$\left\{\matrix{ 0 \le x \le 2 \cr 0 \le y \le \sqrt{2 x - x^2} \cr}\right\}$$

Draw the region described by the inequalities. Do the "number" inequalities first. $0 \le x \le 2$ tells you the region is between the vertical lines $x = 0$ and $x = 2$ .

The y-inequalities $0 \le y \le \sqrt{2 x - x^2}$ tell you that the top curve for the region is $y = \sqrt{2 x - x^2}$ and the bottom curve is $y = 0$ --- the same kind of thing you do when you used (single) integrals to compute the area between curves.

To recognize $y = \sqrt{2 x - x^2}$ , complete the square:

$$\eqalign{ y & = \sqrt{2 x - x^2} \cr y^2 & = 2 x - x^2 \cr x^2 - 2 x + y^2 & = 0 \cr x^2 - 2 x + 1 + y^2 & = 1 \cr (x - 1)^2 + y^2 & = 1 \cr}$$

$y = \sqrt{2 x - x^2}$ is the top half of a circle of radius 1 centered at $(1, 0)$ . Here's the picture:

$$\hbox{\epsfysize=2.5 in \epsffile{double-integrals-in-polar-4.eps}}$$

Now I describe the region in polar. Convert the circle to polar:

$$\eqalign{ x^2 - 2 x + y^2 & = 0 \cr x^2 + y^2 & = 2 x \cr r^2 & = 2 r \cos \theta \cr r & = 2 \cos \theta \cr}$$

The top half is traced out as $\theta$ goes from 0 to $\dfrac{\pi}{2}$ --- think of a searchlight beam turning to trace out the curve:

$$\hbox{\epsfysize=1.75 in \epsffile{double-integrals-in-polar-5.eps}}$$

Therefore, the polar inequalities are

$$\left\{\matrix{ 0 \le \theta \le \dfrac{\pi}{2} \cr \noalign{\vskip2pt} 0 \le r \le 2 \cos \theta \cr}\right\}$$

So

$$\int_0^2 \int_0^{\sqrt{2 x - x^2}} \sqrt{x^2 + y^2}\,dx\,dy = \int_0^{\pi/2} \int_0^{2 \cos \theta} r \cdot r\,dr\,d\theta = \int_0^{\pi/2} \left[\dfrac{1}{3} r^3\right]_0^{2 \cos \theta}\,d\theta = \dfrac{8}{3} \int_0^{\pi/2} (\cos \theta)^3\,d\theta =$$

$$\dfrac{8}{3} \int_0^{\pi/2} \left(1 - (\sin \theta)^2\right)(\cos \theta)\,d\theta = \dfrac{16}{9}.$$

(I did the $\theta$ integral with the substitution $u = \sin \theta$ .)

Example. Compute the volume of the region $x^2 + y^2 + 1 \le z \le 2$ .

Here is the region:

$$\hbox{\epsfysize=2 in \epsffile{double-integrals-in-polar-6.eps}}$$

The "bowl" is the surface $z = x^2 + y^2 + 1$ .

The intersection of $z = 2$ and $z = x^2 + y^2 + 1$ is

$$2 = x^2 + y^2 + 1, \quad\hbox{or}\quad x^2 + y^2 = 1.$$

This is the curve where the bowl hits the plane, and you can see it's the unit circle (moved up to $z = 2$ ).

Hence, if you project the region down into the x-y plane, you'll get the interior of the circle $x^2 + y^2 = 1$ . I'll convert to polar. The projection is

$$\left\{\matrix{ 0 \le \theta \le 2 \pi \cr 0 \le r \le 1 \cr}\right\}$$

To find the volume, I integrate $\hbox{top} - \hbox{bottom}$ , which is

$$2 - (x^2 + y^2 + 1) = 1 - x^2 - y^2 = 1 - r^2.$$

Since I'm converting to polar, I replace $dx\,dy$ with $r\,dr\,d\theta$ . The volume is

$$V = \int_0^{2 \pi} \int_0^1 (1 - r^2) r\,dr\,d\theta = \int_0^{2 \pi} \int_0^1 (r - r^3)\,dr\,d\theta = \int_0^{2 \pi} \left[\dfrac{1}{2} r^2 - \dfrac{1}{4} r^4\right]_0^1\,d\theta =$$

$$\dfrac{1}{4} \int_0^{2 \pi}\,d\theta = \dfrac{\pi}{2}.\quad\halmos$$

Contact information

Bruce Ikenaga's Home Page

Copyright 2018 by Bruce Ikenaga