Gradient, Divergence, and Curl

The operators named in the title are built out of the del operator

$\nabla = \ihat \pder {} x + \jhat \pder {} y + \khat \pder {} z.$

(It is also called nabla. That always sounded goofy to me, so I will call it "del".)

Del is a formal vector; it has components, but those components have partial derivative operators ( $\pder {} x$ and so on) which want to be fed functions to differentiate. So as a general rule, when you multiply FOO by del, the partial derivative operators differentiate FOO as opposed to multiplying.

First, suppose f is a function. $\nabla f$ is the gradient of f, sometimes denoted $\grad f$ .

Example. Compute the gradient of $f(x, y, z) = x y e^{y^2 z}$ .

$\nabla f = \ihat \pder f x + \jhat \pder f y + \khat \pder f z = \ihat \left(y e^{y^2 z}\right) + \jhat \left(x e^{y^2 z} + 2 x y^2 e^{y^2 z}\right) + \khat \left(x y^3 e^{y^2 z}\right).$

You can also write this as

$\nabla f = \left(y e^{y^2 z}, x e^{y^2 z} + 2 x y^2 e^{y^2 z}, x y^3 e^{y^2 z}\right).\quad\halmos$

$\nabla$ is a vector; what kinds of things can you do with a vector? Well, you can take the dot product of the vector with another vector. If you do that with $\nabla$ , you obtain the divergence:

$\diverg \vec F = \nabla \cdot \vec F.$

For this to make sense, $\vec F$ should be a vector field; since the dot product of two vectors is a number, $\diverg \vec F$ should be a number (that is, a numerical function).

Example. Compute the divergence of $\vec F = (x^2 + y)\ihat + (y^2 - z)\jhat + (z^2 + x)\khat$ .

$\diverg \vec F = \left(\ihat \pder {} x + \jhat \pder {} y + \khat \pder {} z\right)\cdot \left((x^2 + y)\ihat + (y^2 - z)\jhat + (z^2 + x)\khat\right) =$

$\pder {} x (x^2 + y) + \pder {} y (y^2 - z) + \pder {} z (z^2 + x) = 2 x + 2 y + 2 z.\quad\halmos$

What is the divergence of a vector field? If you think of the field as the velocity field of a fluid flowing in three dimensions, then $\diverg \vec F = 0$ means the fluid is incompressible --- for any closed region, the amount of fluid flowing in through the boundary equals the amount flowing out. This result follows from the Divergence Theorem, one of the big theorems of vector integral calculus.

You can take the cross product of two 3-dimensional vectors; if you do this with $\nabla$ , you obtain the curl of a vector field:

$\curl \vec F = \nabla \times \vec F.$

More specfically, suppose $\vec F = (F_1, F_2, F_3)$ . Then

$\nabla \times \vec F = \left|\matrix{ \ihat & \jhat & \khat \cr \pder {} x & \pder {} y & \pder {} z \cr F_1 & F_2 & F_3 \cr}\right|.$

The cross product of two vectors is a vector, so curl takes a vector field to another vector field.

Example. Compute the curl of $\vec F = (x^2 + y)\ihat + (y^2 - z)\jhat + (z^2 + x)\khat$ .

$\curl \vec F = \left|\matrix{ \ihat & \jhat & \khat \cr \pder {} x & \pder {} y & \pder {} z \cr x^2 + y & y^2 - z & z^2 + x \cr}\right|.$

As usual, I'll expand the determinant by cofactors of the first row:

$\ihat \left|\matrix{ \pder {} y & \pder {} z \cr y^2 - z & z^2 + x \cr}\right| - \jhat \left|\matrix{ \pder {} x & \pder {} z \cr x^2 + y & z^2 + x \cr}\right| + \khat \left|\matrix{ \pder {} x & \pder {} y \cr x^2 + y & y^2 - z \cr}\right| =$

$\ihat \left(\pder {} y (z^2 + x) - \pder {} z (y^2 - z)\right) - \jhat \left(\pder {} x (z^2 + x) - \pder {} z (x^2 + y )\right) + \khat \left(\pder {} x (y^2 - z) - \pder {} y (x^2 + y)\right) =$

$(0 - (-1)) \ihat - (1 - 0) \jhat + (0 - 1) \khat = \ihat - \jhat + \khat = (1, -1, 1).\quad\halmos$

What is the curl of a vector field? To make it easier to visualize, suppose $\vec F$ is the velocity field for a fluid flow in the plane (so the z component is 0).

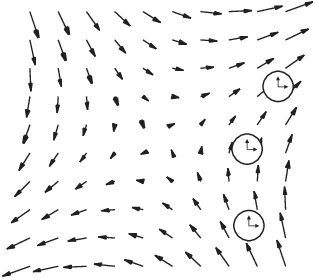
$\hbox{\epsfysize=2.5in \epsffile{gradient-divergence-curl1.eps}}$

Drop a marked float into the flow and let it be carried along by the fluid. Then $\curl \vec F = \vec 0$ means, roughly, that the float doesn't rotate as it moves.

The old name for $\curl \vec F$ was $\rot \vec F$ , the rotation of $\vec F$ . A field with $\rot \vec F = \vec 0$ is said to be irrotational (and this terminology is still used, even though rot has been replaced by curl).

There are many identities involving div, grad, and curl; here is an important one.

Example. Show that $\curl \grad f = \vec 0$ .

$\curl \grad f = \nabla \times \nabla f = \left|\matrix{ \ihat & \jhat & \khat \cr \pder {} x & \pder {} y & \pder {} z \cr \pder f x & \pder f y & \pder f z \cr}\right|.$

You can grind this out and discover that everything cancels by equality of mixed partial derivatives (e.g. $\dfrac{\partial^2 f}{\partial x \partial y} = \dfrac{\partial^2 f}{\partial y \partial x}$ ). But it's easier to operate formally, factoring f out of the last row:

$\left|\matrix{\ihat & \jhat & \khat \cr \pder {} x & \pder {} y & \pder {} z \cr \pder f x & \pder f y & \pder f z \cr}\right| = \left|\matrix{\ihat & \jhat & \khat \cr \pder {} x & \pder {} y & \pder {} z \cr \pder {} x & \pder {} y & \pder {} z \cr}\right|(f).$

But the determinant of a matrix with two equal rows is 0, so the result is $\vec 0$ .

Contact information

Bruce Ikenaga's Home Page