Interchanging the Order of Integration

Consider the iterated integral

$$\dint_D f(x, y)\,dx\,dy.$$

It can be computed by integrating with respect to x first or with respect to y first. In some cases, one order is better than the other. For this reason, it's useful to know how to go from a "bad" order of integration to a "good" order of integration.

Example. Compute $\displaystyle \int_0^1 \int_{\sqrt{y}}^1 \dfrac{1}{\sqrt{x^3 + 1}}\,dx\,dy$ .

As the integral is given, I'd need to integrate first with respect to x. However, I don't know the antiderivative of $\dfrac{1}{\sqrt{x^3 + 1}}$ . I'll interchange the order of integration and integrate first with respect to y.

Step 1: Pull off the limits of integration as inequalities.

$$\left\{\matrix{ 0 \le y \le 1 \cr \sqrt{y} \le x \le 1 \cr}\right\}$$

Step 2: Draw the region defined by the inequalities.

$$\hbox{\epsfysize=1.75 in \epsffile{interchanging-the-order-1.eps}}$$

Step 3: Describe the region by inequalities with the variables in the opposite order.

In the first set of inequalities, y came first. In this set, x will come first. For x, I can take the numerical bounds in the x-direction: $0 \le x \le 1$ .

Next, I need the inequalities for y. y is the vertical variable, so it will be bounded by expressions for the bottom curve and the top curve of the region. The bottom curve is the x-axis, which is $y = 0$ . The top curve is $x = \sqrt{y}$ . Since I'm bounding y, I need to express y in terms of x. Thus, $y = x^2$ .

Therefore, the inequalities for y are $0 \le y \le x^2$ . The new set of inequalities is

$$\left\{\matrix{ 0 \le x \le 1 \cr 0 \le y \le x^2 \cr}\right\}$$

Step 4: Put the inequalities back onto the integral:

$$\int_0^1 \int_0^{x^2} \dfrac{1}{\sqrt{x^3 + 1}}\,dy\,dx = \int_0^1 \dfrac{1}{\sqrt{x^3 + 1}} \int_0^{x^2} \,dy\,dx = \int_0^1 \dfrac{1}{\sqrt{x^3 + 1}}\left[y\right]_0^{x^2}\,dx =$$

$$\int_0^1 \dfrac{x^2}{\sqrt{x^3 + 1}}\,dx = \left[ \dfrac{2}{3} \sqrt{x^3 + 1} \right]_0^1 = \dfrac{2}{3}(\sqrt{2} - 1) = 0.27614 \ldots.\quad\halmos$$

Schematically, here's what's going on:

$$\hbox{integral} \to \hbox{inequalities} \to \hbox{picture} \to \hbox{inequalities} \to \hbox{integral}$$

This is similar to the procedure for converting a double integral to polar coordinates.

Example. Compute the integral by interchanging the order of integration:

$$\int_1^e \int_{\ln y}^1 \cos (e^x - x)\,dx\,dy.$$

Pull off the limits as inequalities:

$$\left\{\matrix{ 1 \le y \le e \cr \ln y \le x \le 1 \cr}\right\}$$

Next, draw the region determined by the inequalities. The inequalities $1 \le y \le e$ imply that the region lies in the horizontal strip between $y = 1$ (bottom) and $y = e$ (top).

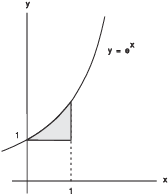
$$\hbox{\epsfysize=1.75 in \epsffile{interchanging-the-order-2.eps}}$$

The inequalities $\ln y \le x \le 1$ give the left-hand and right-hand boundaries, because x is the horizontal variable. The left-hand curve is $x = \ln y$ , or $y = e^x$ . The right-hand curve is $x = 1$ . The region is shown above.

Next, describe the region by inequalities with the variables switched. I'll do x first, since the first set of inequalities had the number bounds on y. The numerical bounds on x are 0 and 1, so $0 \le x \le 1$ .

To get the bounds on y, I look at the bottom curve and the top curve. The bottom curve is the line $y = 1$ . The top curve is $y = e^x$ . Hence, the inequalities for y are $1 \le y \le e^x$ .

The new inequalities are

$$\left\{\matrix{ 0 \le x \le 1 \cr 1 \le y \le e^x \cr}\right\}$$

Put the inequalities back onto the integral:

$$\int_0^1 \int_1^{e^x} \cos (e^x - x)\,dy\,dx = \int_0^1 \cos (e^x - x) \int_1^{e^x}\,dy\,dx = \int_0^1 \cos (e^x - x) \left[ y \right]_1^{e^x}\,dx =$$

$$\int_0^1 (e^x - 1) \cos (e^x - x) \,dx = \int_1^{e-1} (e^x - 1) \cos u \cdot \dfrac{du}{e^x - 1} = \int_1^{e-1} \cos u\,du = \left[\sin u\right]_1^{e-1} =$$

$$\left[u = e^x - x, \quad du = (e^x - 1)\,dx, \quad dx = \dfrac{du}{e^x - 1}; x = 0, \quad u = 1; \quad x = 1, \quad u = e - 1\right]$$

$$\sin (e - 1) - \sin 1 = 0.14767 \ldots.\quad\halmos$$

Example. Express the following sum as a single iterated integral by interchanging the order of integration:

$$\int_0^1 \int_0^y f(x,y)\,dx\,dy + \int_1^2 \int_0^{2-y} f(x,y)\,dx\,dy$$

Pull off the limits as inequalities:

$$\left\{\matrix{ 0 \le y \le 1 \cr 0 \le x \le y \cr}\right\} \quad\hbox{and}\quad \left\{\matrix{ 1 \le y \le 2 \cr 0 \le x \le 2 - y \cr}\right\}$$

Draw the region determined by the inequalities.

$$\hbox{\epsfysize=1.75 in \epsffile{interchanging-the-order-3.eps}}$$

Describe the region by inequalities with the variables switched:

$$\left\{\matrix{ 0 \le x \le 1 \cr x \le y \le 2 - x \cr}\right\}$$

Put the new inequalities back onto the integral:

$$\int_0^1 \int_x^{2-x} f(x,y)\,dy\,dx.\quad\halmos$$

Example. Compute $\displaystyle \int_0^1 \int_y^1 2 \cos (x^2)\,dx\,dy$ .

Pull off the limits as inequalities:

$$\left\{\matrix{ 0 \le y \le 1 \cr y \le x \le 1 \cr}\right\}$$

Draw the region determined by the inequalities.

$$\hbox{\epsfysize=1.75 in \epsffile{interchanging-the-order-4.eps}}$$

Describe the region by inequalities with the variables switched:

$$\left\{\matrix{ 0 \le x \le 1 \cr 0 \le y \le x \cr}\right\}$$

Put the new inequalities back onto the integral:

$$\int_0^1 \int_y^1 2 \cos (x^2)\,dx\,dy = \int_0^1 \int_0^x 2 \cos (x^2)\,dy dx = \int_0^1 2 x \cos (x^2)\,dx =$$

$$\left[u = x^2, \quad du = 2 x\,dx, \quad dx = \dfrac{du}{2 x}; \quad x = 0, \quad u = 0; \quad x = 1, \quad u = 1\right]$$

$$\int_0^1 2 x \cos u \cdot \dfrac{du}{2 x} = \int_0^1 \cos u\,du = \left[\sin u\right]_0^1 = \sin 1 = 0.84147 \ldots.\quad\halmos$$

Contact information

Bruce Ikenaga's Home Page

Copyright 2018 by Bruce Ikenaga