Lagrange Multipliers

The method of Lagrange multipliers deals with the problem of finding the maxima and minima of a function subject to a side condition, or constraint.

Example. Find graphically the highest and lowest points on the plane $x + 2 y + 3 z = 6$ which lie above the circle $x^2 + y^2 = 1$ .

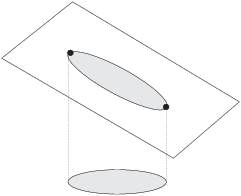
$$\hbox{\epsfysize=1.75 in \epsffile{lagrange-1.eps}}$$

The plane as a whole has no "highest point" and no "lowest point". If you only consider the part of the plane lying above the circle, there is a highest point and a lowest point. These constrained extrema are the highest and lowest points on the oval in the plane that lies above the circle.

How do you locate such constrained extrema? For functions of two variables, I'll provide a heuristic argument based on level curves. (A similar argument works in higher dimensions.)

Suppose you're trying to find the largest and smallest value of $z = f(x, y)$ subject to the constraint $g(x, y) = 0$ . The equation $g(x, y) = 0$ defines a curve in the x-y-plane; I'll draw the constraint curve, together with the level curves for f.

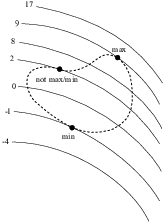
$$\hbox{\epsfysize=2in \epsffile{lagrange-2.eps}}$$

The constraint curve is the dashed curve; the numbers are the "altitude numbers" for the respective level curves. As you walk around the constraint curve, the highest altitude you encounter is 9. It occurs at the point labelled "max". The lowest altitude you encounter is -1. It occurs at the point labelled "min". there is also a pointed

Something interesting happens at the max and at the min. You can see from the picture that at those points, the constraint curve is tangent to a level curve. Why should this happen?

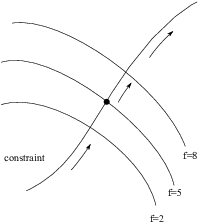
$$\hbox{\epsfysize=2in \epsffile{lagrange-3.eps}}$$

Imagine walking along the constraint curve. As you walk, you note the altitude numbers of the level curves that you pass through, hoping to find a constrained max. Suppose you're at a point where the constraint passes through a level curve (as opposed to being tangent to it). Then (as the picture shows) as you pass through the level curve, you will encounter level curves with higher altitude numbers "on the other side". Therefore, you haven't reached the max yet.

In the context of this picture, the only way you can reach a max is if the constraint curve "turns around" at some point. At the place where it "turns around", it will be tangent to a level curve.

This heuristic argument suggests that we should locate points where the constraint curve is tangent to a level curve. We need a way of locating such points of tangency algebraically.

Note that some points of this type will be neither maxima nor minima. An example of such a point is labelled "not max.min" in the picture above.

What happens, then, at a point of tangency? Recall that the gradient vector at a point is perpendicular to the level curve passing through the point. Hence, $\nabla f$ is perpendicular to the level curve at the point. Moreover, $\nabla g$ is perpendicular to $g(x, y) = 0$ at the point, because $g(x, y) = 0$ is a level curve of the function $z = g(x, y)$ .

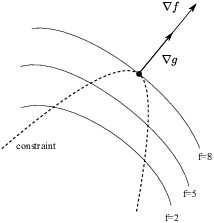
$$\hbox{\epsfysize=2in \epsffile{lagrange-4.eps}}$$

Since the curves are tangent at the point, and since the gradient vectors are perpendicular to the respective curves, the gradient vectors must lie along the same line. Vectors which lie along the same line are multiples. Therefore,

$$\nabla f = \lambda \nabla g \quad\hbox{for some number}\quad \lambda.$$

The number $\lambda$ is the Lagrange multiplier. Some people prefer to use L or l instead.

In other words, to find the points where a constrained max or min could occur, you should locate all points which satisfy

$$\nabla f = \lambda \nabla g \quad\hbox{and}\quad g = 0.$$

The constraint equation is included, because any solution to the problem must satisfy the constraint.

Suppose f and g are functions of x and y. If I expand $\nabla f = \lambda \nabla g$ in component form, the equations are:

$$\pder f x = \lambda \pder g x, \quad \pder f y = \lambda \pder g y, \quad g(x, y) = 0.$$

The first two equations represent, in component form, the multiplier equation $\nabla f = \lambda \nabla g$ . The third equation is the constraint.

You can put $\lambda$ on either the f side or the g side of the first two equations (i.e. on the f side in both or on the g side in both) --- whichever is most convenient. For example, this is also okay:

$$\lambda \pder f x = \pder g x, \quad \lambda \pder f y = \pder g y, \quad g(x, y) = 0.$$

Note that for the purposes of computing the partial derivatives, your constraint must be written in the form $g = 0$ . For instance, if you constraint is given as $x^2 = 4 - y^2$ , then rewrite it as $x^2 + y^2 - 4 = 0$ and take $g(x, y) = x^2 + y^2 - 4$ .

Example. Find the highest and lowest points on the plane

$$z = 2 x + 6 y + 1 \quad\hbox{subject to the constraint}\quad x^2 + y^2 = 40.$$

Write the constraint as $g(x, y) = x^2 + y^2 - 40 = 0$ . Set up the multiplier equations:

$$\eqalign{ \nabla f & = \lambda \nabla g \cr (2, 6) & = (2 x \lambda, 2 y \lambda) \cr}$$

This gives the equations

$$2 = 2 x \lambda, \quad 1 = x \lambda.$$

$$6 = 2 y \lambda, \quad 3 = y \lambda.$$

$$x^2 + y^2 = 40.$$

Note that if $x = 0$ , the first equation gives $2 = 0$ , a contradiction. Hence, $x \ne 0$ , and I may divide by x.

Solve simultaneously:

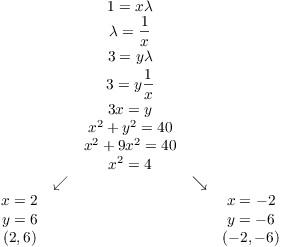
$$\matrix{ & & 1 = x \lambda & & \cr \noalign{\vskip2pt} & & \lambda = \dfrac{1}{x} & & \cr \noalign{\vskip2pt} & & 3 = y \lambda & & \cr \noalign{\vskip2pt} & & 3 = y \dfrac{1}{x} & & \cr \noalign{\vskip2pt} & & 3 x = y & & \cr & & x^2 + y^2 = 40 & & \cr & & x^2 + 9 x^2 = 40 & & \cr & & x^2 = 4 & & \cr & \swarrow & & \searrow & \cr x = 2 & & & & x = -2 \cr y = 6 & & & & y = -6 \cr (2, 6) & & & & (-2, -6) \cr}$$

Notice that when I take square roots in $x^2 = 4$ , I need both the positive and negative square roots of 4, so I get two branches --- one for $x = 2$ and one for $x = -2$ .

Test the points:

$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & \cr & point & & $z = 2 x + 6 y + 1$ & & result & \cr height2pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & \cr & $(2, 6)$ & & 41 & & max & \cr height2pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & \cr & $(-2, -6)$ & & -41 & & min & \cr height2pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} }} $$

In this case, I got a max and a min. This will always be the case if the constraint satisfies a condition called compactness. In general, you may need to give a geometric argument to show that a point is a max or a min. And it's possible for there to be no absolute max or min satisfying a constraint.

Example. Find the maxima and minima of

$$f(x, y) = 6 x y \quad\hbox{subject to the constraint}\quad x^2 + y^2 = 18.$$

Write $g(x, y) = x^2 + y^2 - 9$ . The constraint is $g(x, y) = 0$ . Set up the multiplier equation:

$$\eqalign{ \nabla f & = \lambda \nabla g \cr (6 y, 6 x) & = \lambda (2 x, 2 y) \cr}$$

Together with the constraint, this yields the equations

$$6 y = 2 x \lambda, \quad 3 y = x \lambda.$$

$$6 x = 2 y \lambda, \quad 3 x = y \lambda.$$

$$x^2 + y^2 = 18.$$

Note that if $x = 0$ , the first equation gives $3 y = 0$ , so $y = 0$ . But $(0, 0)$ does not satisfy $x^2 + y^2 = 18$ , so this is not possible. Thus, $x \ne 0$ , and a similar argument shows that $y \ne 0$ . This means that in solving the equations below, I may divide by x or y.

Solve the equations simultaneously:

$$\matrix{ & & & & 3 y = x \lambda & & & & \cr \noalign{\vskip2pt} & & & & \lambda = \dfrac{3 y}{x} & & & & \cr \noalign{\vskip2pt} & & & & 3 x = y \lambda & & & & \cr \noalign{\vskip2pt} & & & & 3 x = y \dfrac{3 y}{x} & & & & \cr \noalign{\vskip2pt} & & & & x^2 = y^2 & & & & \cr & & & & x^2 + y^2 = 18 & & & & \cr & & & & 2 x^2 = 18 & & & & \cr & & & & x^2 = 9 & & & & \cr & & & \swarrow & & \searrow & & & \cr & & x = 3 & & & & x = -3 & & \cr & & y^2 = 9 & & & & y^2 = 9 & & \cr & \swarrow & \downarrow & & & & \downarrow & \searrow & \cr y = 3 & & y = -3 & & & & y = 3 & & y = -3 \cr (3, 3) & & (3, -3) & & & & (-3, 3) & & (-3, -3) \cr}$$

Once again, every time I take a square root I get a positive and a negative root, and I get two branches.

Test the points:

$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & \cr & point & & $f(x, y) = 6 x y$ & & result & \cr height2pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & \cr & $(3, 3)$ & & 54 & & max & \cr height2pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & \cr & $(3, -3)$ & & -54 & & min & \cr height2pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & \cr & $(-3, 3)$ & & -54 & & min & \cr height2pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & \cr & $(-3, -3)$ & & 54 & & max & \cr height2pt & \omit & & \omit & & \omit & \cr \noalign{\hrule} }}\quad\halmos $$

Example. Find the largest and smallest values of $z = x^2 y$ subject to the constraint $x^2 + 8 y^2 = 24$ .

The constraint is $g(x, y) = x^2 + 8 y^2 - 24 = 0$ . Hence, I must solve the equations

$$\eqalignno{ 2 x y = 2 x \lambda & \quad\hbox{or}\quad \quad x(y - \lambda) = 0 & (1) \cr x^2 & = 16 y \lambda & (2) \cr x^2 + 8 y^2 & = 24 & (3) \cr}$$

Notice that in the first equation I can divide out 2 but not x! One of the most common mistakes in solving simultaneously is dividing by something with a variable in it. When you do this, you are liable to drop roots.

In the previous examples, I've organized the work in a "solution tree"; in this example, the tree is a little more complicated, so I'll describe how to set a tree up. While you don't have to do things this way, I recommend it: It will help you avoid going in circles, and remind you to do things like taking both positive and negative square roots.

The rules for setting up a solution tree are roughly as follows:

(i) Use one equation at a time. Don't use an equation twice in the same branch of the tree. (I've number the initial equations to refer to them in the tree, but this isn't necessary.)

I'll use "branch" to refer to a path from the bottom (or wherever you are at a given point) back up to the root of the tree (the equation you started with).

(ii) A branch forks when you take cases. You take cases when you must take square roots, because you must take positive and negative square roots. You also take cases when you have something of the form

$$\hbox{blip} \cdot \hbox{blap} = 0.$$

In this situation, the tree forks into branches with $\hbox{blip} = 0$ and with $\hbox{blap} = 0$ .

(iii) When you've solved for the variables, combine them to get solution points. However, you are only allowed to use information in a single branch which goes from a solved value back to the tree's "root". You may not mix values from different branches, because different branches represent different cases.

This is easier to show than to explain, so look at the work below.

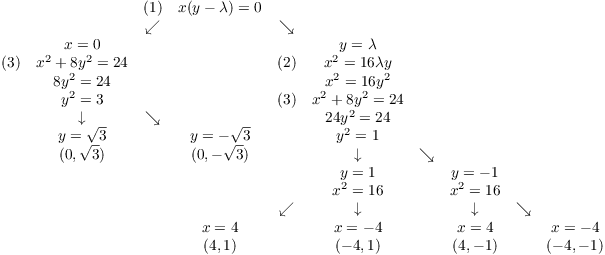
$$\matrix{\textfont0=\eightrm \scriptfont0=\fiverm & & {\rm (1)} & x(y - \lambda) = 0 & & & & & & \cr & & \swarrow & & \searrow & & & & & \cr & x = 0 & & & & y = \lambda & & & & \cr {\rm (3)} & x^2 + 8 y^2 = 24 & & & {\rm (2)} & x^2 = 16\lambda y & & & & \cr & 8 y^2 = 24 & & & & x^2 = 16 y^2 & & & & \cr & y^2 = 3 & & & {\rm (3)} & x^2 + 8 y^2 = 24 & & & & \cr & \downarrow & \searrow & & & 24 y^2 = 24 & & & & \cr & y = \sqrt{3} & & y = -\sqrt{3} & & y^2 = 1 & & & & \cr & (0,\sqrt{3}) & & (0, -\sqrt{3}) & & \downarrow & \searrow & & & \cr & & & & & y = 1 & & y = -1 & & \cr & & & & & x^2 = 16 & & x^2 = 16 & & \cr & & & & \swarrow & \downarrow & & \downarrow & \searrow & \cr & & & x = 4 & & x = -4 & & x = 4 & & x = -4 \cr & & & (4, 1) & & (-4, 1) & & (4, -1) & & (-4, -1) \cr } $$

Notice that the first equation $x (y - \lambda) = 0$ had the form $\hbox{blip} \cdot \hbox{blap} = 0$ , so I split into two branches which I work on separately.

Notice also that I don't mix $x = 4$ and $y = \sqrt{3}$ to get "$(4, \sqrt{3})$ ", for instance, because $x = 4$ and $y = \sqrt{3}$ come from different branches back to the root (the equation $x (y - \lambda) = 0$ ).

Once you've obtained your candidate points, test them by plugging them back into the function you're trying to maximize/minimize. The largest values are the maxima; the smallest values are the minima. Test the points:

$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & $(x, y)$ & & $(0, \sqrt{3})$ & & $(0, -\sqrt{3})$ & & $(4, 1)$ & & $(4, -1)$ & & $(-4, 1)$ & & $(-4, -1)$ & \cr height2pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & $f(x, y)$ & & 0 & & 0 & & 16 & & -16 & & 16 & & -16 & \cr height2pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & & & & & & & max & & min & & max & & min & \cr height2pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} }} $$

The points $(0, \sqrt{3})$ and $(0, -\sqrt{3})$ are neither maxes nor mins.

Example. Find the largest and smallest values of $z = x^2 + 6 y$ subject to the constraint $x^2 + y^2 = 25$ .

The constraint is

$$g(x, y) = x^2 + y^2 - 25.$$

Set up the multiplier equation:

$$\eqalign{ \nabla z & = \lambda \nabla g \cr (2 x, 6) & = \lambda (2 x, 2 y) \cr}$$

This gives

$$2 x = 2 x \lambda, \quad x (1 - \lambda) = 0.$$

$$6 = 2 y \lambda.$$

Solve these together with the constraint:

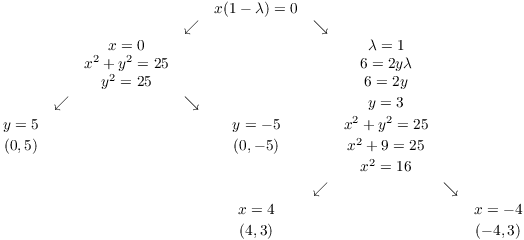
$$\matrix{ & & & & x (1 - \lambda) = 0 & & & & \cr & & & \swarrow & & \searrow & & & \cr & & x = 0 & & & & \lambda = 1 & & \cr & & x^2 + y^2 = 25 & & & & 6 = 2 y \lambda & & \cr & & y^2 = 25 & & & & 6 = 2 y & & \cr \noalign{\vskip2pt} & \swarrow & & \searrow & & & y = 3 & & \cr \noalign{\vskip2pt} y = 5 & & & & y = -5 & & x^2 + y^2 = 25 & & \cr \noalign{\vskip2pt} (0, 5) & & & & (0, -5) & & x^2 + 9 = 25 & & \cr \noalign{\vskip2pt} & & & & & & x^2 = 16 & & \cr \noalign{\vskip2pt} & & & & & \swarrow & & \searrow & \cr \noalign{\vskip2pt} & & & & x = 4 & & & & x = -4 \cr \noalign{\vskip2pt} & & & & \left(4, 3\right) & & & & \left(-4, 3\right) \cr}$$

Test the points:

$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2pt & \omit & & \omit & \cr & point & & $z = x^2 + 6 y$ & \cr height2pt & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & \cr & $(0, 5)$ & & 30 & \cr height2pt & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & \cr & $(0, -5)$ & & -30 & \cr height2pt & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & \cr & $\left(4, 3\right)$ & & 34 & \cr height2pt & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & \cr & $\left(-4, 3\right)$ & & 34 & \cr height2pt & \omit & & \omit & \cr \noalign{\hrule} }}\quad\halmos $$

In the same way, if you want to optimize $w = f(x, y, z)$ subject to a constraint $g(x, y, z) = 0$ , the multiplier equations are

$$\pder f x = \lambda \pder g x, \quad \pder f y = \lambda \pder g y, \quad \pder f z = \lambda \pder g z, \quad g(x, y, z) = 0.$$

You may put $\lambda$ on either side of the first three equations (i.e. on the f side in all three or on the g side in all three). For example, we can use these equations instead of those above:

$$\lambda \pder f x = \pder g x, \quad \lambda \pder f y = \pder g y, \quad \lambda \pder f z = \pder g z, \quad g(x, y, z) = 0.$$

Example. The picture below shows a constraint curve $g(x, y) = 0$ (the oval). Approximate the largest and smallest values of $z = x + y$ subject to the constraint.

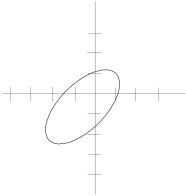
$$\hbox{\epsfysize=1.75 in \epsffile{lagrange-5.eps}}$$

The level curves of $z = x + y$ are lines making an angle of $135^{\circ}$ with the positive x-axis. Since the constrained extrema occur where the level curves are tangent to the oval, we see by sketching that the max is approximately $z = 2$ and the min is approximately $z = -4.5$ .

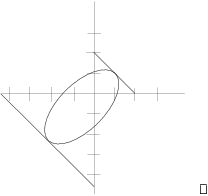
$$\hbox{\epsfysize=1.75 in \epsffile{lagrange-6.eps}}\quad\halmos$$

Example. Find the highest and lowest points on the surface $f(x, y) = x^2 + 2 x y + \dfrac{5}{2}y^2$ which lie above the circle $x^2 + y^2 = 20$ .

I want to find the maxima and minima of f subject to the constraint $g(x, y) = x^2 + y^2 - 20 = 0$ .

$$2 x + 2 y = 2 x\lambda, \quad x + y = \lambda x, \leqno{\rm (1)}$$

$$2 x + 5 y = 2 y\lambda, \leqno{\rm (2)}$$

$$x^2 + y^2 = 20. \leqno{\rm (3)}$$

Solve simultaneously:

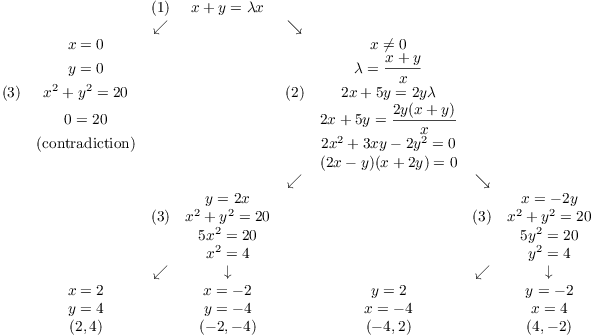
$$\matrix{\textfont0=\eightrm \scriptfont0=\fiverm & & {\rm (1)} & x + y = \lambda x & & & & \cr & & \swarrow & & \searrow & & & \cr & x = 0 & & & & x \ne 0 & & \cr & y = 0 & & & & \lambda = \dfrac{x + y}{x} & & \cr {\rm (3)} & x^2 + y^2 = 20 & & & {\rm (2)} & 2 x + 5 y = 2 y\lambda & & \cr & 0 = 20 & & & & 2 x + 5 y = \dfrac{2 y(x + y)}{x} & & \cr & ({\rm contradiction}) & & & & 2 x^2 + 3 xy - 2 y^2 = 0 & & \cr & & & & & (2 x - y)(x + 2 y) = 0 & & \cr & & & & \swarrow & & \searrow & \cr & & & y = 2 x & & & & x = -2 y \cr & & {\rm (3)} & x^2 + y^2 = 20 & & & {\rm (3)} & x^2 + y^2 = 20 \cr & & & 5 x^2 = 20 & & & & 5 y^2 = 20 \cr & & & x^2 = 4 & & & & y^2 = 4 \cr & & \swarrow & \downarrow & & & \swarrow & \downarrow \cr & x = 2 & & x = -2 & & y = 2 & & y = -2 \cr & y = 4 & & y = -4 & & x = -4 & & x = 4 \cr & (2, 4) & & (-2, -4) & & (-4, 2) & & (4, -2) \cr } $$

Notice that to solve the first equation for $\lambda$ , I needed to divide by x. However, this is illegal if $x = 0$ . So I get two branches: One for the case $x = 0$ , and the other for the case $x \ne 0$ .

If you divide an equation by an expression containing a variable, you must take two cases to account for the possibility of division by 0: One case is when the expression is 0, the other case is when the expression in not 0.

It happens that the $x = 0$ branch gives a contradiction. When this happens, the branch ends, as the left-hand branch did.

Test the points:

$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr & $(x, y)$ & & $(2, 4)$ & & $(-2, -4)$ & & $(-4, 2)$ & & $(4, -2)$ & \cr height2pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr & $f(x, y)$ & & 60 & & 40 & & 10 & & 10 & \cr height2pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr & & & max & & max & & min & & min & \cr height2pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} }}\quad\halmos $$

Example. Find the largest and smallest values of $w = x + 2 y^2 - z^2$ subject to the constraint $x^2 + 4 y^2 + 2 z^2 = 17$ .

The constraint is $g(x, y, z) = x^2 + 4 y^2 + 2 z^2 - 17 = 0$ . The multiplier equations are

$$\lambda = 2 x, \leqno{\rm (1)}$$

$$4\lambda y = 8 y, \quad y(\lambda - 2) = 0, \leqno{\rm (2)}$$

$$-2\lambda z = 4 z, \quad z(\lambda + 2) = 0, \leqno{\rm (3)}$$

$$x^2 + 4 y^2 + 2 z^2 = 17. \leqno{\rm (4)}$$

Solve simultaneously:

$$\overfullrule=0pt \matrix{\textfont0=\eightrm \scriptfont0=\fiverm & & & {\rm (1)} & \lambda = 2 x & & & & \cr & & & {\rm (2)} & y(\lambda - 2) = 0 & & & & \cr & & & & y(2 x - 2) = 0 & & & & \cr & & & \swarrow & & \searrow & & & \cr & & y = 0 & & & & x = 1 & & \cr & {\rm (3)} & z(\lambda + 2) = 0& & & {\rm (3)} & z(\lambda + 2) = 0 & & \cr & & z(2 x + 2) = 0 & & & & z(2 x + 2) = 0 & & \cr & & \downarrow & \searrow & & & \downarrow & \searrow & \cr & & z = 0 & & x = -1 & & 2 x + 2 = 0 & & z = 0 \cr & {\rm (4)} & x^2 + 4 y^2 + 2 z^2 = 17 & {\rm (4)} & x^2 + 4 y^2 + 2 z^2 = 17 & & x = -1 & {\rm (4)} & x^2 + 4 y^2 + 2 z^2 = 17 \cr & & x^2 = 17 & & z^2 = 8 & & ({\rm contradiction}) & & \downarrow \cr & \swarrow & \downarrow & & \downarrow & \searrow & & & \downarrow \cr x = \sqrt{17} & & x = -\sqrt{17} & & z = \sqrt{8} & & z = -\sqrt{8} & & \downarrow \cr (\sqrt{17}, 0, 0) & & (-\sqrt{17}, 0, 0) & & (-1, 0,\sqrt{8}) & & (-1, 0, -\sqrt{8}) & & \downarrow \cr & & & & & & & & y^2 = 4 \cr & & & & & & & \swarrow & \downarrow \cr & & & & & & y = 2 & & y = -2 \cr & & & & & & (1, 2, 0) & & (1, -2, 0) \cr } $$

$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \ # \ \hfil \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & $(x, y, z)$ & & $(\sqrt{17}, 0, 0)$ & & $(-\sqrt{17}, 0, 0)$ & & $(-1, 0, \sqrt{8})$ & & $(-1, 0, -\sqrt{8})$ & & $(1, 2, 0)$ & & $(1, -2, 0)$ & \cr height2pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & $w(x, y, z)$ & & $\sqrt{17}$ & & $-\sqrt{17}$ & & -9 & & -9 & & 9 & & 9 & \cr height2pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & & & & & & & min & & min & & max & & max & \cr height2pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} }} $$

Example. A rectangular box with no top is to be constructed using 300 square inches of cardboard. Find the dimensions of the box which has the largest volume.

Suppose the dimensions of the bottom of the box are x and y and the height of the box is z.

$$\hbox{\epsfysize=1.75in \epsffile{lagrange-7.eps}}$$

The cardboard is used to make the sides and the bottom, and the total area is

$$300 = x y + 2 x z + 2 y z.$$

The volume is

$$V = x y z.$$

I want to maximize V.

The constraint is $g(x, y, z) = x y + 2 x z + 2 y z - 300 = 0$ .

Set up the multiplier equation:

$$\eqalign{ \nabla A & = \lambda \nabla g \cr (y z, x z, x y) & = \lambda (y + 2 z, x + 2 z, 2 x + 2 y) \cr}$$

I get the following equations:

$$y z = \lambda (y + 2 z).$$

$$x z = \lambda (x + 2 z).$$

$$x y = \lambda (2 x + 2 y).$$

$$x y + 2 x z + 2 y z = 300.$$

Note that $x, y, z > 0$ . If any of the dimensions equals 0, I get a volume of 0, and it's obvious I can produce some box satisyfing the constraint with positive volume.

In particular, $y + 2 z$ , $x + 2 z$ , and $2 x + 2 y$ are all positive, and I may divide by any of them.

Solve the equations simultaneously:

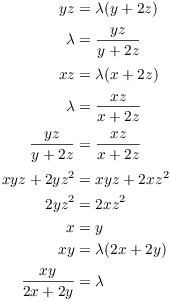
$$\eqalign{ y z &= \lambda (y + 2 z) \cr \noalign{\vskip2pt} \lambda & = \dfrac{y z}{y + 2 z} \cr \noalign{\vskip2pt} x z & = \lambda (x + 2 z) \cr \noalign{\vskip2pt} \lambda & = \dfrac{x z}{x + 2 z} \cr \noalign{\vskip2pt} \dfrac{y z}{y + 2 z} & = \dfrac{x z}{x + 2 z} \cr \noalign{\vskip2pt} x y z + 2 y z^2 & = x y z + 2 x z^2 \cr 2 y z^2 & = 2 x z^2 \cr x & = y \cr x y & = \lambda (2 x + 2 y) \cr \noalign{\vskip2pt} \dfrac{x y}{2 x + 2 y} & = \lambda \cr}$$

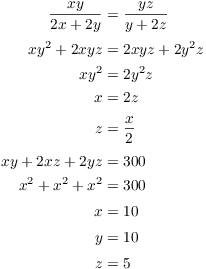
$$\eqalign{ \dfrac{x y}{2 x + 2 y} & = \dfrac{y z}{y + 2 z} \cr \noalign{\vskip2pt} x y^2 + 2 x y z & = 2 x y z + 2 y^2 z \cr x y^2 & = 2 y^2 z \cr x & = 2 z \cr \noalign{\vskip2pt} z & = \dfrac{x}{2} \cr \noalign{\vskip2pt} x y + 2 x z + 2 y z & = 300 \cr x^2 + x^2 + x^2 & = 300 \cr \noalign{\vskip2pt} x & = 10 \cr \noalign{\vskip2pt} y & = 10 \cr \noalign{\vskip2pt} z & = 5 \cr}$$

The critical point is $\left(10, 10, 5\right)$ .

To see that this is a max, note that V can be made arbitrarily small in the following way. Since $z = \dfrac{300 - x y}{2 x + 2 y}$ ,

$$V = \dfrac{(300 - x y)(x y)}{2 x + 2 y}.$$

Let $x = y$ . This becomes

$$V = \dfrac{(300 - x^2)(x^2)}{2 x + 2 x} = \dfrac{x (300 - x^2)}{4}.$$

Letting $x \to 0$ , I have $\dfrac{x (300 - x^2)}{4} \to 0$ .

Thus, if the critical point represents either a max or a min, it must certainly represent a max.

Contact information

Bruce Ikenaga's Home Page

Copyright 2022 by Bruce Ikenaga