Limits and Continuity

I'll give the precise definition of a limit so that you can see the similarity to the definition you saw in single-variable calculus. The first definition is a technical point which you don't need to worry about too much. It simply ensures if we take a limit as $x \to c$ , that x can approach c through a set where the function is defined.

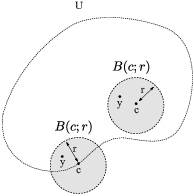
Definition. Let U be a subset of $\real^n$ . A point $c \in \real^n$ is an accumulation point of U if for every $r > 0$ , the open ball $B(c; r)$ contains a point $y \in U$ other than c.

$B(c; r)$ is the set of points in $\real^n$ which are less than r units from c:

$$B(c; r) = \{x \in \real^n \mid r > \|x - c\|\}.$$

$$\hbox{\epsfysize=1.75in \epsffile{limits-and-continuity-1.eps}}$$

Definition. Let $f: U \to \real^m$ be a function defined on $U \subset \real^n$ , and let c be an accumulation point of U. Then $\displaystyle \lim_{x \to c} f(x) = L$ means:

For every $\epsilon > 0$ , there is a $\delta$ , such that

$$\hbox{if}\quad \delta > \|x - c\| > 0, \quad\hbox{then}\quad \epsilon > \|f(x) - L\|.$$

Many results you know about limits from single-variable calculus have analogs for functions of several variables.

Proposition. Suppose $f, g: U \to \real$ where $U \subset \real^n$ . Let c be an accumulation point of U, and let $k \in \real$ . Then:

(a) $\displaystyle \lim_{x \to c} [f(x) + g(x)] = \lim_{x \to c} f(x) + \lim_{x \to c} g(x)$ .

(b) $\displaystyle \lim_{x \to c} k \cdot f(x) = k \cdot \lim_{x \to c} f(x)$ .

(c) $\displaystyle \lim_{x \to c} f(x) \cdot g(x) = [\lim_{x \to c} f(x)] [\lim_{x \to c} g(x)]$ .

(d) $\displaystyle \lim_{x \to c} \dfrac{f(x)}{g(x)} = \dfrac{\lim_{x \to c} f(x)}{\lim_{x \to c} g(x)}$ , provided that $\displaystyle \lim_{x \to c} g(x) \ne 0$ .

All of these results mean that if the limits on the right side are defined, then so is the limit on the left side, and the two sides are equal.

I won't try to state all of the easy results on limits that generalize to functions of several variables. You will see many of them proven in a course in real analysis. Let's look at some of the complications that result from being able to approach a point in more than one dimension.

Example. Compute $\displaystyle \lim_{(x, y) \to (-1, 2)} \dfrac{5 x + y + 1}{2 x - y}$ .

I can compute the limit by plugging in. (This is another way of saying that $f(x, y) = \dfrac{5 x + y + 1}{2 x - y}$ is continuous at $(3, 1)$ .) Thus.

$$\lim_{(x, y) \to (3, 1)} \dfrac{5 x + y + 1}{2 x - y} = \dfrac{5 \cdot 3 + 1 + 1}{2 \cdot 3 - 1} = \dfrac{17}{5}.\quad\halmos$$

Example. Compute $\displaystyle \lim_{(x, y, z) \to (4, 1, 2)} (x + 3 y) e^{-z}$ .

I can compute the limit by plugging in.

$$\lim_{(x, y, z) \to (4, 1, 2)} (x + 3 y) e^{-z} = (4 + 3 \cdot 1) e^{-2} = 7 e^{-2}.\quad\halmos$$

Example. Compute $\displaystyle \lim_{(x, y) \to (0, 0)} \dfrac{5 x y - 2 y^2}{x^2 + y^2}$ .

Substituting $(x, y) = (0, 0)$ yields the indeterminate form $\dfrac{0}{0}$ .

Here's the graph of the function. Notice that as $(x, y) \to (0, 0)$ the height seems to approach one value along the "ridgeline" while it approaches another value along the "valley":

$$\hbox{\epsfysize=1.75in \epsffile{limits-and-continuity-2.eps}}$$

This leads me to believe that the limit is undefined.

To prove this, I try to find different ways of approaching $(0, 0)$ which give different limits. Specifically, I try to pick different curves through $(0, 0)$ which make $\dfrac{5 x y - 2 y^2}{x^2 + y^2}$ simplify to different values. In this case, I try the x-axis, which is $y = 0$ , and the y-axis, which is $x = 0$ .

Set $y = 0$ and let $x \to 0$ . I have

$$\lim_{x \to 0} \dfrac{5 x \cdot 0 - 2 \cdot 0^2}{x^2 + 0^2} = \lim_{x \to 0} \dfrac{0}{x^2} = \lim_{x \to 0} 0 = 0.$$

Set $x = 0$ and let $y \to 0$ . I have

$$\lim_{y \to 0} \dfrac{5 \cdot 0 \cdot y - 2 y^2}{0^2 + y^2} = \lim_{y \to 0} \dfrac{-2 y^2}{y^2} = \lim_{y \to 0} (-2) = -2.$$

Since $\dfrac{5 x y - 2 y^2}{x^2 + y^2}$ approaches different numbers depending on how $(x, y)$ approaches $(0, 0)$ , the limit is undefined.

Example. Compute $\displaystyle \lim_{(x, y) \to (0, 0)} \dfrac{3 x^4 y}{x^8 + y^2}$ .

Substituting $(x, y) = (0, 0)$ yields the indeterminate form $\dfrac{0}{0}$ .

Here's the graph of the function. It is a little harder to tell from the graph what is happening near the origin.

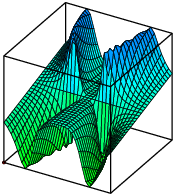
$$\hbox{\epsfysize=1.75in \epsffile{limits-and-continuity-3.eps}}$$

It turns out that the limit is undefined. To show this, I'll approach $(0, 0)$ along a line and along a curve.

If you approach $(0, 0)$ along the line $y = 0$ , you get

$$\lim_{(x, y) \to (0, 0)} \dfrac{3 x^4 y}{x^8 + y^2} = \lim_{x \to 0} \dfrac{3 \cdot x^4 \cdot 0}{x^8 + 0^2} = \lim_{x \to 0} \dfrac{0}{x^8} = \lim_{x \to 0} 0 = 0$$

Next, I notice that $x^4 \cdot x^4 = x^8$ and $(x^4)^2 = x^8$ . Thus, I can get multiple "$x^8$ " terms by setting $y = x^4$ .

If you approach $(0, 0)$ along the curve $y = x^4$ , you get

$$\lim_{(x, y) \to (0, 0)} \dfrac{3 x^4 y}{x^8 + y^2} = \lim_{x \to 0} \dfrac{3 x^4 \cdot x^4}{x^8 + (x^4)^2} = \lim_{x \to 0} \dfrac{3 x^8}{2 x^8} = \lim_{x \to 0} \dfrac{3}{2} = \dfrac{3}{2}.$$

Since $\dfrac{3 x^4 y}{x^8 + y^2}$ approaches different numbers depending on how $(x, y)$ approaches $(0, 0)$ , the limit is undefined.

Example. Compute $\displaystyle \lim_{(x, y) \to (0, 0)} \dfrac{x^2 y^2}{x^2 + y^2}$ by converting to polar coordinates.

Let $x = r \cos \theta$ and $y = r \sin \theta$ . Then

$$\dfrac{x^2 y^3}{x^2 + y^2} = \dfrac{(r \cos \theta)^2 (r \sin \theta)^2}{(r \cos \theta)^2 + (r \sin \theta)^2} = \dfrac{r^4 (\cos \theta)^2 (\sin \theta)^2}{r^2} = r^2 (\cos \theta)^2 (\sin \theta)^2.$$

Then

$$\lim_{(x, y) \to (0, 0)} \dfrac{2 x y^3}{x^2 + y^2} = \lim_{r \to 0} r^2 (\cos \theta)^2 (\sin \theta)^2 = 0.\quad\halmos$$

Example. Compute $\displaystyle \lim_{(x, y, z) \to (0, 0, 0)} \dfrac{x^2 + y^2 + z^2}{5 y^2 + z^2}$ .

I try to find different curves through $(0, 0)$ which make $\dfrac{x^2 + y^2 + z^2}{5 y^2 + z^2}$ simplify to different values.

If you approach $(0, 0, 0)$ along the line $y = z$ , $x = 0$ , you get

$$\lim_{(x, y, z) \to (0, 0, 0)} \dfrac{x^2 + y^2 + z^2}{5 y^2 + z^2} = \lim_{z \to 0} \dfrac{0^2 + z^2 + z^2}{5 z^2 + z^2} = \lim_{z \to 0} \dfrac{2 z^2}{6 z^2} = \lim_{z \to 0} \dfrac{1}{3} = \dfrac{1}{3}.$$

If you approach $(0, 0, 0)$ along the line $x = y = z$ , you get

$$\lim_{(x, y, z) \to (0, 0, 0)} \dfrac{x^2 + y^2 + z^2}{5 y^2 + z^2} = \lim_{x \to 0} \dfrac{x^2 + x^2 + x^2}{5 x^2 + x^2} = \lim_{x \to 0} \dfrac{3 x^2}{6 x^2} = \lim_{x \to 0} \dfrac{1}{2} = \dfrac{1}{2}.$$

Since you get different limits by approaching $(0, 0, 0)$ in different ways, $\displaystyle \lim_{(x, y, z) \to (0, 0, 0)} \dfrac{x^2 + y^2 + z^2}{5 y^2 + z^2}$ is undefined.

Definition. Let $f: U \to \real^m$ , where $U \subset \real^n$ , and let $c \in U$ . Then f is continuous at c if

$$\lim_{x \to c} f(x) = f(c).$$

Remark. Some authors will say a function $\real^n \to \real^m$ is not continous at a point where the function isn't defined. For example, the function f defined by $f(x) = \dfrac{1}{x - 1}$ has (natural) domain $x \ne 1$ . These authors will say that f is not continuous at $x = 1$ , with similar terminology for multivariable functions. I'll avoid doing this: It seems inappropriate to talk about whether a function does or does not have a property like continuity at the point where there is no function!

I'll only consider continuity (or lack of continuity) at points in a function's domain.

Example. A function $\real^2 \to \real$ is defined by

$$f(x, y) = \cases{ \dfrac{x + 3 y}{2 x + 5 y} & if $(x, y) \ne (2, 1)$ \cr \noalign{\vskip2pt} \dfrac{4}{9} & if $(x, y) = (2, 1)$ \cr}.$$

Is f continuous at $(2, 1)$ ?

$$\lim_{(x, y) \to (2, 1)} f(x, y) = \lim_{(x, y) \to (2, 1)} \dfrac{x + 3 y}{2 x + 5 y} = \dfrac{5}{9}.$$

However, $f(2, 1) = \dfrac{4}{9}$ ,

Since $\displaystyle \lim_{(x, y) \to (2, 1)} f(x, y) \ne f(2, 1)$ , it follows that f is not continuous at $(2, 1)$ .

Contact information

Bruce Ikenaga's Home Page

Copyright 2018 by Bruce Ikenaga