Matrices

A matrix is a rectangular array of numbers:

$$\left[\matrix{1 & 2 & \pi \cr -41 & \sqrt{2} & 3.7 \cr}\right] \quad \left[\matrix{42 \cr 0 \cr -13 \cr}\right] \quad \left[\matrix{1 & a & a^2 \cr 1 & b & b^2 \cr 1 & c & c^2 \cr}\right]$$

Actually, the entries can be more general than numbers, but you can think of the entries as numbers to start. I'll give a rapid account of basic matrix arithmetic; you can find out more in a course in linear algebra.

Definition. (a) If A is a matrix, $A_{ij}$ is the element in the $i^{\rm th}$ row and $j^{\rm th}$ column.

(b) If a matrix has m rows and n columns, it is said to be an $m \times n$ matrix, and m and n are the dimensions. A matrix with the same number of rows and columns is a square matrix.

(c) If A and B are $m \times n$ matrices, then $A = B$ if their corresponding entries are equal; that is, if $A_{ij} = B_{ij}$ for all i and j.

Note that matrices of different dimensions can't be equal.

(d) If A and B are $m \times n$ matrices, their sum $A + B$ is the matrix obtained by adding corresponding entries of A and B:

$$(A + B)_{ij} = A_{ij} + B_{ij}.$$

(e) If A is a matrix and k is a number, the product of A by k is the matrix obtained by multiplying the entries of A by k:

$$(k A)_{ij} = k \cdot A_{ij}.$$

(f) The $m \times n$ zero matrix is the matrix all of whose entries are 0.

(g) If A is a matrix, then $-A$ is the matrix obtained by negating the entries of A.

(h) If A and B are $m \times n$ matrices, their difference $A - B$ is

$$A - B = A + (-B).$$

Example. Suppose

$$A = \left[\matrix{ 1 & 2 & 3 \cr 4 & 5 & \pi \cr}\right].$$

(a) What are the dimensions of A?

(b) What is $A_{21}$ ?

(a) A is a $2 \times 3$ matrix: It has 2 rows and 3 columns.

(b) $A_{21}$ is the element in row 2 and column 1, so $A_{21} = 4$ .

The following results are unsurprising, in the sense that things work the way you'd expect them to given your experience with numbers. (This is not always the case with matrix multiplication, which I'll discuss later.)

Proposition. Suppose p and q are numbers and A, B, and C are $m \times n$ matrices.

(a) (Associativity) $(A + B) + C = A + (B + C)$ .

(b) (Commutativity) $A + B = B + A$ .

(c) (Zero Matrix) If 0 denotes the $m \times n$ zero matrix, then

$$0 + A = A \quad\hbox{and}\quad A + 0 = A.$$

(d) (Additive Inverses) If 0 denotes the $m \times n$ zero matrix, then

$$A + (-A) = 0 \quad\hbox{and}\quad (-A) + A = 0.$$

(e) (Distributivity)

$$p (A + B) = p A + p B \quad\hbox{and}\quad (p + q) A = p A + q A.$$

Proof. Matrix equality says that two matrices are equal if their corresponding entries are equal. So the proofs of these results amount to considering the entries of the matrices on the left and right sides of the equations.

By way of example, I'll prove (b). I must show that $A + B$ and $B + A$ have the same entries.

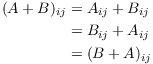
$$\eqalign{ (A + B)_{ij} & = A_{ij} + B_{ij} \cr & = B_{ij} + A_{ij} \cr & = (B + A)_{ij} \cr}$$

The first and third equalities used the definition of matrix addition. The second equality used commutativity of addition for numbers.

Matrix multiplication is more complicated. Your first thought might be to multiply two matrices the way you add matrices --- that is, by multiplying corresponding entries. That is not how matrices are multiplied, and the reason is that it isn't that useful. What is useful is a more complicated definition which uses dot products.

Suppose A is an $m \times n$ matrix and B is an $n \times p$ matrix. Note that the number of columns of A must equal the number of rows of B. To form the matrix product $A B$ , I have to tell you what the $(i, j)^{\rm th}$ entry of $A B$ is. Here is the description in words: $(A B)_{i j}$ is the dot product of the $i^{\rm th}$ row of A and the $j^{\rm th}$ column of B.

The resulting matrix $A B$ will be an $m \times p$ matrix.

This is best illustrated by examples.

Example. Compute the matrix product

$$\left[\matrix{2 & -1 \cr 5 & 1 \cr}\right] \left[\matrix{1 & -1 & 3 \cr 8 & 0 & 4 \cr}\right].$$

This is the product of a $2 \times 2$ matrix and a $2 \times 4$ matrix. The product should be a $2 \times 4$ matrix. I'll show the computation of the entries in the product one-by-one. For each entry in the product, I take the dot product of a row of the first matrix and a column of the second matrix.

$(2, -1) \cdot (1, 8) = -6$ :

$$\hbox{\epsfysize=0.4in \epsffile{matrices-1.eps}}$$

$(2, -1) \cdot (-1, 0) = -2$ :

$$\hbox{\epsfysize=0.4in \epsffile{matrices-2.eps}}$$

$(2, -1) \cdot (3, 4) = 2$ :

$$\hbox{\epsfysize=0.4in \epsffile{matrices-3.eps}}$$

$(5, 1) \cdot (1, 8) = 13$ :

$$\hbox{\epsfysize=0.4in \epsffile{matrices-4.eps}}$$

$(5, 1) \cdot (-1, 0) = -5$ :

$$\hbox{\epsfysize=0.4in \epsffile{matrices-5.eps}}$$

$(5, 1) \cdot (3, 4) = 19$ :

$$\hbox{\epsfysize=0.4in \epsffile{matrices-6.eps}}$$

Thus,

$$\left[\matrix{2 & -1 & \cr 5 & 1 \cr}\right] \left[\matrix{1 & -1 & 3 \cr 8 & 0 & 4 \cr}\right] = \left[\matrix{-6 & -2 & 2 \cr 13 & -5 & 19 \cr}\right].\quad\halmos$$

Example. Multiply the following matrices:

$$\left[\matrix{ 3 & -5 \cr 3 & -6 \cr}\right] \left[\matrix{ 4 & -2 \cr 4 & -5 \cr}\right]$$

$$\left[\matrix{ 3 & -5 \cr 3 & -6 \cr}\right] \left[\matrix{ 4 & -2 \cr 4 & -5 \cr}\right] = \left[\matrix{ -8 & 19 \cr -12 & 24 \cr}\right].\quad\halmos$$

Example. Multiply the following matrices:

$$\left[\matrix{ 4 & -6 & -3 & 4 \cr}\right] \left[\matrix{-2 \cr -5 \cr 0 \cr -2 \cr}\right]$$

$$\left[\matrix{ 4 & -6 & -3 & 4 \cr}\right] \left[\matrix{-2 \cr -5 \cr 0 \cr -2 \cr}\right] = \left[\matrix{14 \cr}\right].\quad\halmos$$

Note that this is essentially the dot product of two 4-dimensional vectors.

Example. Multiply the following matrices:

$$\left[\matrix{ -4 & 1 \cr 2 & 5 \cr 1 & 0 \cr}\right] \left[\matrix{ -1 & 0 & -3 \cr -1 & 2 & 4 \cr}\right]$$

$$\left[\matrix{ -4 & 1 \cr 2 & 5 \cr 1 & 0 \cr}\right] \left[\matrix{ -1 & 0 & -3 \cr -1 & 2 & 4 \cr}\right] = \left[\matrix{ 3 & 2 & 16 \cr -7 & 10 & 14 \cr -1 & 0 & -3 \cr}\right].\quad\halmos$$

The formal definition of matrix multiplication involves summation notation. Suppose A is an $m \times n$ matrix and B is an $n \times p$ matrix, so the product $A B$ makes sense. To tell what $A B$ is, I have to say what a typical entry of the matrix is. Here's the definition:

$$(A B)_{i j} = \sum_{k = 1}^n A_{i k} B_{k j}.$$

Let's relate this to the concrete description I gave above. The summation variable is k. In $A_{i k}$ , this is the column index. So with the row index i fixed, I'm running through the columns from $k = 1$ to $k = n$ . This means that I'm running down the $i^{\rm th}$ row of A.

Likewise, in $B_{k j}$ the variable k is the row index. So with the column index j fixed, I'm running through the rows from $k = 1$ to $k = n$ . This means that I'm running down the $j^{\rm th}$ column of B.

Since I'm forming products $A_{i k} B_{k j}$ and then adding them up, this means that I'm taking the dot product of the $i^{\rm th}$ row of A and the $j^{\rm th}$ column of B, as I described earlier.

Proofs of matrix multiplication properties involve this summation definition, and as a consequence they are often a bit messy with lots of subscripts flying around. I'll let you see them in a linear algebra course.

Definition. The $n \times n$ identity matrix is the matrix with 1's down the main diagonal (the diagonal going from upper left to lower right) and 0's elsewhere.

For instance, the $4 \times 4$ identity matrix is

$$\left[\matrix{ 1 & 0 & 0 & 0 \cr 0 & 1 & 0 & 0 \cr 0 & 0 & 1 & 0 \cr 0 & 0 & 0 & 1 \cr}\right].$$

Proposition. Suppose A, B, and C are matrices (with dimensions compatible for multiplication in all the products below), and let k be a number.

(a) (Associativity) $(A B) C = A (B C)$ .

(b) (Identity) $A I = A$ and $I A = I$ (where I denotes an $n \times n$ identity matrix compatible for multiplication in the respective products).

(c) (Zero) $A 0 = 0$ and $0 A = 0$ (where 0 denotes a zero matrix compatible for multiplication in the respective products).

(d) (Scalars) $k (A B) = (k A) B = A (k B)$ .

(e) (Distributivity)

$$A(B + C) = A B + A C \quad\hbox{and}\quad (A + B) C = A C + B C.$$

I'll omit the proofs, which are routine but a bit messy (as they involve the summation definition of matrix multiplication).

Note that commutativity of multiplication is not listed as a property. In fact, it's false --- and it one of a number of ways in which matrix multiplication does not behave in ways you might expect. It's important to make a note of things which behave in unexpected ways.

Example. Give specific $2 \times 2$ matrices A and B such that $A B \ne B A$ .

There are many examples. For instance,

$$\left[\matrix{1 & 2 \cr 1 & 0 \cr}\right] \left[\matrix{0 & 1 \cr 1 & 2 \cr}\right] = \left[\matrix{2 & 5 \cr 0 & 1 \cr}\right].$$

$$\left[\matrix{0 & 1 \cr 1 & 2 \cr}\right] \left[\matrix{1 & 2 \cr 1 & 0 \cr}\right] = \left[\matrix{1 & 0 \cr 3 & 2 \cr}\right].\quad\halmos$$

This shows that matrix multiplication is not commutative.

Example. Give specific $2 \times 2$ matrices A and B such that $A \ne 0$ , $B \ne 0$ , but $A B = 0$ .

There are many possibilities. For instance,

$$\left[\matrix{1 & 0 \cr 1 & 0 \cr}\right] \left[\matrix{0 & 0 \cr 3 & -7 \cr}\right] = \left[\matrix{0 & 0 \cr 0 & 0 \cr}\right].\quad\halmos$$

Example. Give specific $2 \times 2$ nonzero matrices A. B, and C such that $A B = A C$ but $B \ne C$ .

There are lots of examples. For instance,

$$\left[\matrix{0 & 1 \cr 0 & 1 \cr}\right] \left[\matrix{1 & 2 \cr 0 & 0 \cr}\right] = \left[\matrix{0 & 0 \cr 0 & 0 \cr}\right] \quad\hbox{and}\quad \left[\matrix{0 & 1 \cr 0 & 1 \cr}\right] \left[\matrix{3 & 4 \cr 0 & 0 \cr}\right] = \left[\matrix{0 & 0 \cr 0 & 0 \cr}\right].$$

But

$$\left[\matrix{1 & 2 \cr 0 & 0 \cr}\right] \ne \left[\matrix{3 & 4 \cr 0 & 0 \cr}\right].\quad\halmos$$

This example shows that you can't "divide" or "cancel" A from both sides of the equation. It works in some cases, but not in all cases.

Definition. Let A be an $n \times n$ matrix. The inverse of A is a matrix $A^{-1}$ which satisfies

$$A A^{-1} = I \quad\hbox{and}\quad A^{-1} A = I.$$

(I is the $n \times n$ identity matrix.) A matrix which has an inverse is invertible.

Remark. (a) If a matrix has an inverse, it is unique.

(b) Not every matrix has an inverse. Determinants provide a criterion for telling whether a matrix is invertible: An $n \times n$ real matrix is invertible if and only if its determinant is nonzero.

Proposition. Suppose A and B are invertible $n \times n$ matrices. Then:

(a) $(A^{-1})^{-1} = A$ .

(b) $(A B)^{-1} = B^{-1} A^{-1}$ .

Proof. I'll prove (b).

$$[B^{-1} A^{-1}] (A B) = B^{-1} I B = B^{-1} B = I.$$

$$(A B) [B^{-1} A^{-1}] = A I A^{-1} = A A^{-1} = I.$$

This shows that $B^{-1} A^{-1}$ is the inverse of $A B$ , because it multiplies $A B$ to the identity matrix in either order.

In general, the most efficient way to find the inverse of a matrix is to use row reduction ( Guassian elimination), which you will learn about in a linear algebra course. But we can give an easy formula for $2 \times 2$ matrices.

Proposition. Consider the real matrix

$$A = \left[\matrix{a & b \cr c & d \cr}\right].$$

Suppose $ad - bc \ne 0$ . Then

$$A^{-1} = \dfrac{1}{a d - b c} \left[\matrix{d & -b \cr -c & a \cr}\right].$$

Proof. Just compute:

$$\dfrac{1}{a d - b c} \left[\matrix{d & -b \cr -c & a \cr}\right] \left[\matrix{a & b \cr c & d \cr}\right] = \dfrac{1}{a d - b c} \left[\matrix{a d - b c & 0 \cr 0 & ad - b c \cr}\right] = \left[\matrix{1 & 0 \cr 0 & 1 \cr}\right].$$

You can check that you also get the identity if you multiply in the opposite order.

Example. Find the inverse of $\displaystyle \left[\matrix{4 & -3 \cr 5 & 1 \cr}\right]$ .

$$\left[\matrix{4 & -3 \cr 5 & 1 \cr}\right]^{-1} = \dfrac{1}{(4)(1) - (-3)(5)} \left[\matrix{1 & 3 \cr -5 & 4 \cr}\right] = \dfrac{1}{19} \left[\matrix{1 & 3 \cr -5 & 4 \cr}\right].\quad\halmos$$

Example. Use matrix inversion to solve the system of equations:

$$\eqalign{ 2 x + 7 y & = 3 \cr x + 10 y & = -1 \cr}$$

You can write the system in matrix form:

$$\left[\matrix{2 & 7 \cr 1 & 10 \cr}\right] \left[\matrix{x \cr y \cr}\right] = \left[\matrix{3 \cr -1 \cr}\right].$$

(Multiply out the left side for yourself and see that you get the original two equations.) Now the inverse of the $2 \times 2$ matrix is

$$\left[\matrix{2 & 7 \cr 1 & 10 \cr}\right]^{-1} = \dfrac{1}{13} \left[\matrix{10 & -7 \cr -1 & 2 \cr}\right].$$

Multiply the matrix equation above on the left of both sides by the inverse:

$$\eqalign{ \dfrac{1}{13} \left[\matrix{10 & -7 \cr -1 & 2 \cr}\right]\left[\matrix{2 & 7 \cr 1 & 10 \cr}\right] \left[\matrix{x \cr y \cr}\right] & = \dfrac{1}{13} \left[\matrix{10 & -7 \cr -1 & 2 \cr}\right] \left[\matrix{3 \cr -1 \cr}\right] \cr \noalign{\vskip2pt} \left[\matrix{1 & 0 \cr 0 & 1 \cr}\right] \left[\matrix{x \cr y \cr}\right] & = \dfrac{1}{13} \left[\matrix{37 \cr -5 \cr}\right] \cr \noalign{\vskip2pt} \left[\matrix{x \cr y \cr}\right] & = \dfrac{1}{13} \left[\matrix{37 \cr -5 \cr}\right] \cr}$$

That is, $x = \dfrac{37}{13}$ and $y = -\dfrac{5}{13}$ .

Contact information

Bruce Ikenaga's Home Page

Copyright 2017 by Bruce Ikenaga