Maxima and Minima for Functions of Two Variables

For a function of one variable $y = f(x)$ , you look for local maxima and minima at critical points --- points where the derivative $\der y x$ is zero. You do something similar to find maxima and minima for functions of two variables.

A point $(a, b)$ is a local max if $f(a, b) \ge f(x, y)$ for all points $(x, y)$ "near" $(a, b)$ . If you want to rule out "ties", then you have to require instead that $f(a, b) > f(x, y)$ for all points $(x, y)$ "near" $(a, b)$ . In this case, $(a, b)$ is a strict local maximum.

Similarly, a point $(a, b)$ is a local min if $f(a, b) \le f(x, y)$ for all points $(x, y)$ "near" $(a, b)$ . Again, to rule out "ties", you'd require instead that $f(a, b) < f(x, y)$ for all points $(x, y)$ "near" $(a, b)$ . In this case, $(a, b)$ is a strict local minimum.

Proposition. Suppose f is defined on an open set containing $(a, b)$ and is differentiable at $(a, b)$ . If $(a, b)$ is a local max or a local min, then

$$\pder f x (a, b) = 0 \quad\hbox{and}\quad \pder f y (a, b) = 0.$$

Proof. If $(a, b)$ is a local max, then it is a local max of $f(x, b)$ , a function of one variable x. Then $\pder f x (a, b) = 0$ by the result on local maxima from single variable calculus. A similar argument shows that $\pder f y (a, b) = 0$ .

A critical point which is neither a local max nor a local min is a saddle.

Thus, to find local maxima or minima, locate the critical points by solving these equations simultaneously:

$$\pder f x = 0 \quad\hbox{and}\quad \pder f y = 0.$$

Example. Use graphs to describe the critical points of $z = x^2 + y^2$ , $z = 1 - x^2 - y^2$ , $z = x^2 - y^2$ , and $z = x^2$ .

$z = x^2 + y^2$ has a local minimum at $(0, 0)$ .

$$\hbox{\epsfysize=1.75 in \epsffile{max-min-two-variables-1.eps}}$$

$z = 1 - x^2 - y^2$ has a local maximum at $(0, 0)$ .

$$\hbox{\epsfysize=1.75 in \epsffile{max-min-two-variables-2.eps}}$$

$z = x^2 - y^2$ has a saddle point at $(0, 0)$ .

$$\hbox{\epsfysize=1.75 in \epsffile{max-min-two-variables-3.eps}}$$

$z = x^2$ has a line of critical points along $x = 0$ . They are local minima, but not strict local minima.

$$\hbox{\epsfysize=1.75 in \epsffile{max-min-two-variables-4.eps}}$$

Once you've located the critical points, you must determine whether they are maxes, mins, or saddles. We have an analog of the Second Derivative Test for functions of one variable.

Theorem. Suppose f is differentiable on an open set containing a critical point $(a, b)$ . Suppose the second partial derivatives are continuous.

Define

$$\Delta = \left(\pdertwo f x\right)\left(\pdertwo f y\right) - \left(\pdertwom f x y\right)^2.$$

Then:

(a) If $\Delta < 0$ , then $(a, b)$ is a saddle (neither a max nor a min).

(b) If $\Delta > 0$ and $\pdertwo f x > 0$ , then $(a, b)$ is a min.

(c) If $\Delta > 0$ and $\pdertwo f x < 0$ , then $(a, b)$ is a max.

(d) If $\Delta = 0$ , the test fails. (This doesn't mean the point is neither a max nor a min --- it means there is no conclusion.)

Remarks. In (b) and (c), you can use "$\pdertwo f y$ " instead of "$\pdertwo f x$ ", because if $\Delta > 0$ the two must have the same sign.

To see that $\Delta = 0$ gives no conclusion, consider $f(x, y) = x^4 + y^4$ . You can check that $(0, 0)$ is a critical point and that $\Delta = 0$ at $(0, 0)$ . However, $(0, 0)$ is a minimum. For $f(0, 0) = 0$ , but if $(x, y) \ne 0$ , then $x^4 + y^4 > 0$ . Hence, every point $(x, y) \ne (0, 0)$ gives a larger value for f than $(0, 0)$ .

Proof. (Sketch) I'll sketch the argument for this test in the case where $\Delta > 0$ .

There is a Taylor expansion for functions of two variables:

$$f(a + h, b + k) = f(a, b) + f_x(a, b) \cdot h + f_y(a, b) \cdot k + \dfrac{1}{2!} \left(f_{x x}(c, d) \cdot h^2 + 2 f_{x y}(c, d) \cdot h k + f_{y y}(c, d) \cdot k^2\right).$$

Here $(c, d)$ is a point on the segment from $(a, b)$ to $(a + h, b + k)$ .

Since $(a, b)$ is a critical point, $f_x = f_y = 0$ , and the series becomes

$$f(a + h, b + k) = f(a, b) + \dfrac{1}{2!} \left(f_{x x}(c, d) \cdot h^2 + 2 f_{x y}(c, d) \cdot h k + f_{y y}(c, d) \cdot k^2\right).$$

To save writing, let

$$A = f_{x x}(c, d), \quad B = f_{x y}(c, d), \quad C = f_{y y}(c, d).$$

The series can then be written

$$f(a + h, b + k) = f(a, b) + \dfrac{1}{2!} \left(A \cdot h^2 + 2 B \cdot h k + C \cdot k^2\right).$$

As long as h and k are small, I can assume that the second derivatives (and hence $\Delta$ ) have the same signs at $(a, b)$ and $(c, d)$ . I'll consider the case where $\Delta = A C - B^2 > 0$ . Note that A and C must be both positive or both negative. For if one is positive and one is negative, then $A C$ is negative, and $A C - B^2 < 0$ , contrary to our assumption. So suppose that A and C are both positive. Then I can write

$$\eqalign{ A \cdot h^2 + 2 B \cdot h k + C \cdot k^2 & = \dfrac{1}{A} \left(A^2 \cdot h^2 + 2 A B \cdot h k + A C k^2\right) \cr & = \dfrac{1}{A} \left(A^2 \cdot h^2 + 2 A B \cdot h k + B^2 \cdot k^2 + A C k^2 - B^2 \cdot k^2\right) \cr & = \dfrac{1}{A} \left[(A h + B k)^2 + (A C - B^2) k^2\right] \cr}$$

Since $A > 0$ and $A C - B^2 > 0$ , the last term is positive. I have

$$f(a + h, b + k) = f(a, b) + \dfrac{1}{2!} (\hbox{positive stuff}).$$

That is, $f(a + h, b + k) > f(a, b)$ for small h and k. This says that points close to $(a, b)$ give bigger f's, so $(a, b)$ must be a min.

Note that if $A < 0$ , then $\dfrac{1}{A} \left[(A h + B k)^2 + (A C - B^2) k^2\right]$ is negative (because the stuff in the brackets is positive). Then

$$f(a + h, b + k) = f(a, b) + \dfrac{1}{2!} (\hbox{negative stuff}).$$

This says that points close to $(a, b)$ give smaller f's, so $(a, b)$ must be a max.

The argument that $\Delta < 0$ yields a saddle is more involved, so I'll omit it.

Example. Locate and classify the critical points of

$$z = (x - 5)^2 + (y + 8)^2.$$

First, compute the partials:

$$\pder f x = 2 (x - 5), \quad \pder f y = 2 (y + 8).$$

$$\pdertwo f x = 2, \quad \pdertwom f x y = 0, \quad \pdertwo f y = 2.$$

Find the critical points:

$$\eqalign{ \pder f x & = 0 \cr \noalign{\vskip2pt} 2 (x - 5) & = 0 \cr x & = 5 \cr}$$

$$\eqalign{ \pder f y & = 0 \cr \noalign{\vskip2pt} 2 (y + 8) & = 0 \cr y & = -8 \cr}$$

The critical point is $(5, -8)$ .

$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & point & & $\pdertwo f x$ & & $\pdertwo f y$ & & $\pdertwom f x y$ & & $\Delta$ & & result & \cr height2pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & $(5, -8)$ & & 2 & & 2 & & 0 & & 4 & & min & \cr height2pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} }} $$

Here's a picture of the surface. You can see the min pretty clearly.

$$\hbox{\epsfysize=1.5in \epsffile{max-min-two-variables-5.eps}}\quad\halmos$$

Example. Locate and classify the critical points of

$$z = 3 x^2 - 2 x + 7 y^2 - 4 y - 8 x y.$$

First, compute the partials:

$$\pder f x = 6 x - 2 - 8 y, \quad \pder f y = 14 y - 4 - 8 x.$$

$$\pdertwo f x = 6, \quad \pdertwom f x y = -8, \quad \pdertwo f y = 14.$$

Find the critical points:

$$\eqalign{ \pder f x & = 0 \cr \noalign{\vskip2pt} 6 x - 2 - 8 y & = 0 \cr 3 x - 4 y & = 1 \cr}$$

$$\eqalign{ \pder f y & = 0 \cr \noalign{\vskip2pt} 14 y - 4 - 8 x & = 0 \cr -4 x + 7 y & = 2 \cr}$$

Multiply $3 x - 4 y = 1$ by 4, multiply $-4 x + 7 y = 2$ by 3, then add the equations:

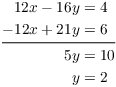
$$\eqalign{ 12 x - 16 y & = 4 \cr -12 x + 21 y & = 6 \cr \noalign{\vskip2pt \hrule \vskip2pt} 5 y & = 10 \cr y & = 2 \cr}$$

Then

$$\eqalign{ 3 x - 4 \cdot 2 & = 1 \cr x & = 3 \cr}$$

The critical point is $(3, 2)$ .

$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & point & & $\pdertwo f x$ & & $\pdertwo f y$ & & $\pdertwom f x y$ & & $\Delta$ & & result & \cr height2pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & $(3, 2)$ & & 6 & & 14 & & -8 & & 20 & & min & \cr height2pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} }} $$ Here's a picture of the surface. In this picture, the min isn't that evident.

$$\hbox{\epsfysize=1.5in \epsffile{max-min-two-variables-6.eps}}\quad\halmos$$

Example. Locate and classify the critical points of

$$z = 3 x y - x^3 - y^3.$$

First, compute the partials:

$$\pder f x = 3 y - 3 x^2, \quad \pder f y = 3 x - 3 y^2,$$

$$\pdertwo f x = -6 x, \quad \pdertwom f x y f = 3, \quad \pdertwo f y = -6 y.$$

Set the first partials equal to zero and do a little simplification:

$$3 y - 3 x^2 = 0, \quad y = x^2, \eqno{\rm (1)}$$

$$3 x - 3 y^2 = 0, \quad x = y^2. \eqno{\rm (2)}$$

It's okay to divide out common factors which are numbers, but you should avoid dividing by something with a variable in it --- unless you're certain the expression cannot be zero.

I'll solve the equations simultaneously using a solution tree. Start with one of the equations --- in this case, it doesn't matter which one.

$$\matrix{ & {\rm (1)} & y = x^2 & & \cr & {\rm (2)} & x = y^2 & & \cr & & x = x^4 & & \cr & & x^4 - x = 0 & & \cr & & x(x^3 - 1) = 0 & & \cr & & x(x - 1)(x^2 + x + 1) = 0 & & \cr & \swarrow & \downarrow & \searrow & \cr x = 0 & & x = 1 & & \hbox{no roots} \cr y = 0 & & y = 1 & & \cr (0, 0) & & (1, 1) & & \cr}$$

Every time I have an equation $(\hbox{FOO}) \cdot (\hbox{BAR}) = 0$ , I get two cases --- $(\hbox{FOO}) = 0$ and $(\hbox{BAR}) = 0$ --- and the tree splits into two branches. (In this case, I had a three-way split, but one branch closed up because there were no solutions.)

I continue working down a branch until I've solved for x and y. Notice that you bring in each of the original equations just once. This will help you avoid going in circles.

Finally, you should not combine values from different branches. For example, I can't put $x = 1$ together with $y = 0$ to get $(1, 0)$ .

Now test the critical points:

$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & point & & $\pdertwo f x$ & & $\pdertwo f y$ & & $\pdertwom f x y f$ & & $\Delta$ & & result & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & $(0, 0)$ & & 0 & & 0 & & 3 & & -9 & & saddle & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & $(1, 1)$ & & -6 & & -6 & & 3 & & 27 & & max & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} }} $$

Using the table, it's easy to remember $\Delta$ --- it's the second column times the third, minus the square of the fourth. Notice that $\Delta > 0$ means the point is either a max or a min. To decide which it is, look at $\pdertwo f x$ . (This may seem asymmetric, but in fact, if $\Delta > 0$ then $\pdertwo f x$ and $\pdertwo f y$ have the same sign.)

Here's a picture of the surface. I've deformed it a bit to exaggerate the critical points.

$$\hbox{\epsfysize=1.75 in \epsffile{max-min-two-variables-7.eps}}\quad\halmos$$

Example. Locate and classify the critical points of

$$z = x^4 - 2 x^2 + y^2 - 10.$$

First, compute the partials:

$$\pder f x = 4 x^3 - 4 x, \quad \pder f y = 2 y,$$

$$\pdertwo f x = 12 x^2 - 4, \quad \pdertwom f x y f = 0, \quad \pdertwo f y = 2.$$

Set the first partials equal to zero:

$$4 x^3 - 4 x = 0, \quad x(x - 1)(x + 1) = 0, \eqno{\rm (1)}$$

$$2 y = 0, \quad y = 0. \eqno{\rm (2)}$$

Solve simultaneously:

$$\matrix{& {\rm (2)} & y = 0 & & \cr & {\rm (1)} & x(x - 1)(x + 1) = 0 & & \cr & \swarrow & \downarrow & \searrow & \cr x = 0 & & x = 1 & & x = -1 \cr (0, 0) & & (1, 0) & & (-1, 0) \cr}$$

Test the critical points:

$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & point & & $\pdertwo f x$ & & $\pdertwo f y$ & & $\pdertwom f x y f$ & & $\Delta$ & & result & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & $(0, 0)$ & & -4 & & 2 & & 0 & & -8 & & saddle & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & $(1, 0)$ & & 8 & & 2 & & 0 & & 16 & & min & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & $(-1, 0)$ & & 8 & & 2 & & 0 & & 16 & & min & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} }} $$

Here's a picture of the surface, deformed to exaggerate the critical points:

$$\hbox{\epsfysize=1.75 in \epsffile{max-min-two-variables-8.eps}}\quad\halmos$$

Example. Locate and classify the critical points of

$$z = \dfrac{2}{3}x^3 - x^2 - xy^2 + \dfrac{2}{3}y^3.$$

First, compute the partials:

$$\pder f x = 2 x^2 - 2 x - y^2, \quad \pder f y = -2 xy + 2 y^2,$$

$$\pdertwo f x = 4 x - 2, \quad \pdertwom f x y f = -2 y, \quad \pdertwo f y = -2 x + 4 y.$$

Set the first partials equal to zero:

$$2 x^2 - 2 x - y^2 = 0, \eqno{\rm (1)}$$

$$-2 xy + 2 y^2 = 0, \quad y(-x + y) = 0. \eqno{\rm (2)}$$

Solve simultaneously:

$$\matrix{ & & & & {\rm (1)} & y(-x + y) = 0 & & & & & \cr & & & \swarrow & & & & \searrow & & & \cr & & y = 0 & & & & & & y = x & & \cr & {\rm (2)} & 2 x^2 - 2 x - y^2 = 0 & & & & & {\rm (2)} & 2 x^2 - 2 x - y^2 = 0 & & \cr & & 2 x^2 - 2 x = 0 & & & & & & x^2 - 2 x = 0 & & \cr & & x(x - 1) = 0 & & & & & & x(x - 2) = 0 & & \cr & \swarrow & & \searrow & & & & \swarrow & & \searrow & \cr x = 0 & & & & x = 1 & & x = 0 & & & & x = 2 \cr (0, 0) & & & & (1, 0) & & y = 0 & & & & y = 2 \cr & & & & & & (0, 0) & & & & (2, 2) \cr}$$

Test the critical points:

$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & point & & $\pdertwo f x$ & & $\pdertwo f y$ & & $\pdertwom f x y f$ & & $\Delta$ & & result & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & $(0, 0)$ & & -2 & & 0 & & 0 & & 0 & & test fails & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & $(1, 0)$ & & 2 & & -2 & & 0 & & -4 & & saddle & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & $(2, 2)$ & & 6 & & 4 & & -4 & & 8 & & min & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} }} $$

Here's a picture of the surface, again deformed to exaggerate the critical points:

$$\hbox{\epsfysize=1.75 in \epsffile{max-min-two-variables-9.eps}}\quad\halmos$$

Example. Locate and classify the critical points of

$$z = \dfrac{1}{9}y^4 - 2 x y^2 - 3 x^2 + \dfrac{3}{2} x^4.$$

Compute the partial derivatives:

$$\pder z x = -2 y^2 - 6 x + 6 x^3, \quad \pder z y = \dfrac{4}{9}y^3 - 4 xy,$$

$$\pdertwo f x = -6 + 18 x^2, \quad \pdertwom f x y f = -4 y, \quad \pdertwo f y = \dfrac{4}{3}y^2 - 4 x.$$

Set the first partials equal to zero:

$$-2 y^2 - 6 x + 6 x^3 = 0, \quad -y^2 - 3 x + 3 x^3 = 0,\eqno{\rm (1)}$$

$$\dfrac{4}{9}y^3 - 4 xy = 0, \quad y^3 - 9 xy = 0, \quad y(y^2 - 9 x) = 0. \eqno{\rm (2)}$$

Solve simultaneously:

$$\matrix{& & {\rm (2)} & y(y^2 - 9 x) = 0 & & & \cr & \swarrow & & & & \searrow & \cr {\rm (a)} & & & & & & {\rm (b)} \cr}$$

$$\matrix{& & {\rm (a)} & & \cr & & y = 0 & & \cr & {\rm (1)} & -y^2 - 3 x + 3 x^3 = 0 & & \cr & & 3 x^3 - 3 x = 0 & & \cr & & x(x - 1)(x + 1) = 0 & & \cr & \swarrow & \downarrow & \searrow & \cr x = 0 & & x = 1 & & x = -1 \cr (0, 0) & & (1, 0) & & (-1, 0) \cr}$$

$$\matrix{& & {\rm (b)} & & \cr & & y^2 - 9 x = 0 & & \cr & {\rm (1)} & -y^2 - 3 x + 3 x^3 = 0 & & \cr & & -9 x - 3 x + 3 x^3 = 0 & & \cr & & 3 x^2 - 12 x = 0 & & \cr & & x(x - 2)(x + 2) = 0 & & \cr & \swarrow & \downarrow & \searrow & \cr x = 0 & & x = 2 & & x = -2 \cr y^2 = 0 & & y^2 = 18 & & y^2 = -18 \cr \matrix{y = 0 \cr (0, 0) \cr} & & \matrix{& \swarrow & \searrow & \cr y = \sqrt{18} & & & y = -\sqrt{18} \cr (2,\sqrt{18}) & & & (2, -\sqrt{18}) \cr} & & \contra \cr}$$

Test the critical points:

$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & point & & $\pdertwo f x$ & & $\pdertwo f y$ & & $\pdertwom f x y f$ & & $\Delta$ & & result & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & $(0, 0)$ & & 0 & & 0 & & 0 & & 0 & & test fails & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & $(1, 0)$ & & 12 & & -4 & & 0 & & -48 & & saddle & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & $(-1, 0)$ & & 12 & & 4 & & 0 & & 48 & & min & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & $(2,\sqrt{18})$ & & 66 & & 8 & & $-12 \sqrt{2}$ & & $-12 \sqrt{2}$ & & saddle & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & $(2, -\sqrt{18})$ & & 66 & & 8 & & $12 \sqrt{2}$ & & $12 \sqrt{2}$ & & min & \cr height2 pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} }} $$

Here's a picture of the surface, again deformed to exaggerate the critical points:

$$\hbox{\epsfysize=1.75 in \epsffile{max-min-two-variables-10.eps}}\quad\halmos$$

Contact information

Bruce Ikenaga's Home Page

Copyright 2018 by Bruce Ikenaga