Multiple Integrals

In this section, I'm going to describe the theoretical background behind multiple integrals. Even though I'm not going to give proofs, the terms and definitions are technical, and you don't need to know them in detail for a course in multivariable calculus. What you should be able to see is the resemblance to the definition of the Riemann integral you saw in single-variable calculus. Focus on the big picture and don't get lost in the technicalities.

In multivariable calculus, we focus on integrals in $\real^2$ (double integrals) and in $\real^3$ (triple integrals). One point of the discussion here is that the theory is essentially the same for both --- and for integrals in higher dimensions, and also for the integrals you've already seen in your first calculus course. So when we discuss double or triple integrals, we only have to consider the differences caused by working in 2 or 3 dimensions.

Definition. A closed box in $\real^n$ consists of the set of points $(x_1, x_2, \ldots, x_n)$ satisfying a set of inequalities

$\eqalign{ a_1 \le & x_1 \le b_1 \cr a_2 \le & x_2 \le b_2 \cr & \vdots \cr a_n \le & x_n \le b_n \cr}$

In this case, we write

$B = [a_1, b_1] \times [a_2, b_2] \times \cdots \times [a_n, b_n].$

This is called an n-fold Cartesian product of the intervals.

The volume of the box B defined above is

$v(B) = (b_1 - a_1) (b_2 - a_2) \dots (b_n - a_n).$

Thus, a box in $\real$ is an interval. A box in $\real^2$ is a rectangle. A box in $\real^3$ is a rectangular parallelepiped --- i.e. what you normally think of as a "box" in the real world. And so on in higher dimensions.

$\hbox{\epsfysize=2.5in \epsffile{multiple-integrals-1.eps}}$

The word "volume" is used generically regardless of the dimension of the box, just so we have one word for a box's "size". So the "volume" of an interval is its length . The "volume" of a box $[a_1, b_1] \times [a_2, b_2]$ is its area as a rectangle. And so on.

Definition. A partition of an interval $a \le x \le b$ is a sequence of points

$s_0 = a \le s_1 \le \cdots \le s_m = b.$

Suppose a closed box B is given by

$B = [a_1, b_1] \times [a_2, b_2] \times \cdots \times [a_n, b_n].$

A partition of B in $\real^n$ consists of a collection of partitions , , ..., of , , ..., .

A partition of B decomposes B into a union of sub-boxes of the form

$B' = [s_1, t_1] \times [s_2, t_2] \times \cdots \times [s_n, t_n].$

Here is a sub-box in the partition of .

It is easy to get lost in all the variables and subscripts, but the basic ideas are simple.

You saw partitions of intervals in discussing integrals in single-variable calculus. A partition of a box is essentially a decompositon of a box into lots of smaller boxes, which fit together to make the big box.

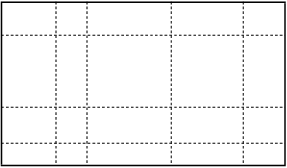
$\hbox{\epsfysize=1.5in \epsffile{multiple-integrals-2.eps}}$

Definition. Let X be a set of points in $\real$ .

(a) The least upper bound of X is the smallest number which is greater than or equal to all the numbers in X. It is denoted $\sup X$ .

(b) The greatest lower bound of X is the largest number which is smaller than or equal to all the numbers in X. It is denoted $\inf X$ .

$\hbox{\epsfysize=1.5in \epsffile{multiple-integrals-3.eps}}$

Definition. Let $X \subset \real^n$ , and let $f: X \to \real$ . Then f is bounded if there is a number M such that for all $x \in X$ .

Definition. Let B be a box in $\real^n$ , and let $f: B \to \real$ be a bounded function. Let P be a partition of B.

If is a sub-box of P, let

$m_{B'}(f) = \inf \{f(x) \mid x \in B'\} \quad\hbox{and}\quad M_{B'}(f) = \sup \{f(x) \mid x \in B'\}.$

The lower sum of f on B relative to the partition P is

$L(f, P) = \sum_{B'} m_{B'}(f) \cdot v(B').$

The upper sum of f on B relative to the partition P is

$U(f, P) = \sum_{B'} M_{B'}(f) \cdot v(B').$

$m_{B'}(f)$ is roughly the smallest value of f on and $M_{B'}(f)$ is roughly the largest value of f on . I say "roughly" because these values might only be approached by f on , not attained.

The upper and lower sums are like the upper and lower rectangle sums you saw in single-variable calculus. There the lower sum was the sum of rectangles built using the smallest values of f on each subinterval, and the upper sum was the sum of rectangles built using the largest values of f on each subinterval.

After all this terminology, I can define the integral of a function.

Definition. Let B be a closed box in $\real^n$ , and let $f: B \to \real^n$ . The function f is integrable if:

(a) f is bounded.

(b) $\sup \{L(f, P)\} = \inf \{U(f, P)\}$ , where the $\sup$ and $\inf$ are taken over all partitions of B.

If f is integrable, the common value $\sup \{L(f, P)\} = \inf \{U(f, P)\}$ is the integral of f on B and is denoted $\displaystyle \int_B f$ .

Note that " $\displaystyle \int_B f$ " doesn't have any variables in it. When we evaluate an integral as an iterated integral, we'll introduce variables as usual. But it's worth remembering that the variables in an integral are "dummy variables" --- so, for example,

$\int_0^1 x^2\,dx = \int_0^1 p^2\,dp.$

The definition of integrable function can be hard to use directly. For many applications the following result is more easily applicable.

Theorem. Let B be a closed box in $\real^n$ , and let $f: B \to \real$ be a bounded function.

f is integrable if and only if the points of discontinuity of f form a set of measure 0.

A set has measure 0 if, roughly speaking, it is "small" relative to its containing space. Some easy examples: A finite set of points has measure 0. In $\real^2$ , the boundary of a closed rectangle has measure 0.

Thus, this result says a bounded function without "too many" discontinuities is integrable.

Many of the usual properties of integrals hold.

Theorem. Let B be a box in $\real^n$ , let $f, g: B \to \real$ be integrable functions on B, and let $c \in \real$ . Then:

(a) $\displaystyle \int_B (f + g) = \int_B f + \int_B g$ .

(b) $\displaystyle \int_B c \cdot f = c \cdot \int_B f$ .

$\int_B f \le \int_B g.\quad\halmos$

Suppose you want to integrate over a set A which is not a closed rectangle. The characteristic function of A is

$\chi_A(x) = \cases{ 1 & if $x \in A$ \cr 0 & if $x \notin A$ \cr}.$

Thus, $\chi_A$ is "on" (equal to 1) if you're in A, and is "off" (equal to 0) if you're not.

If f is integrable on a closed box B and $A \subset B$ , the integral of f on A is defined by

$\int_A f = \int_B f \cdot \chi_A.$

$\hbox{\epsfysize=1.5in \epsffile{multiple-integrals-4.eps}}$

As long as A is reasonably behaved, f will be integrable on A. Specifically, f is integrable on A if and only if the boundary of A has measure 0 (terminology I've discussed above).

Contact information

Bruce Ikenaga's Home Page