Spherical Coordinates

Spherical coordinates represent points in $\real^3$ using three numbers: $(\rho, \theta, \phi)$ .

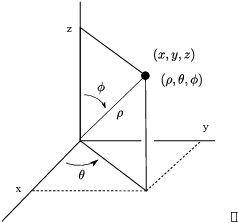
$\hbox{\epsfysize=2in \epsffile{spherical-coordinates-1.eps}}\quad\halmos$

$\rho$ is the distance from to the point.

$\theta$ is "the polar coordinate $\theta$ " --- that is, project the ray from the origin to the point down to a ray $\vec{r}$ in the x-y plane. Measure the angle $\theta$ from the positive x-axis to $\vec{r}$ in the usual way.

$\phi$ is the angle from the positive z-axis to the ray from the origin to the point.

The conversion equations are

$x = \rho \sin \phi \cos \theta, \quad y = \rho \sin \phi \sin \theta, \quad z = \rho \cos \phi.$

Note also that

$\rho^2 = x^2 + y^2 + z^2.$

However, if you're converting the coordinates of a single point from one coordinate system to another, the best thing is to draw a picture and use trigonometry.

Example. A point has rectangular coordinates $(-2, 2, 2\sqrt{6})$ . Find its spherical coordinates.

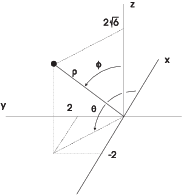
$\hbox{\epsfysize=1.75in \epsffile{spherical-coordinates-2.eps}}$

First, $\theta = \dfrac{3\pi}{4}$ . Since $r = 2 \sqrt{2}$ and $z = 2 \sqrt{6}$ , $\rho = 4 \sqrt{2}$ by Pythagoras.

$\tan \phi = \dfrac{r}{z} = \dfrac{2 \sqrt{2}}{2 \sqrt{6}} = \dfrac{1}{\sqrt{3}}.$

So $\phi = \dfrac{\pi}{6}$ .

The spherical coordinates are $\left(4 \sqrt{2}, \dfrac{3 \pi}{4}, \dfrac{\pi}{6}\right)$ .

Note: If a point lies below the x-y-plane, $\phi$ will be greater than $\dfrac{\pi}{2}$ . In that case, you can't use $\sin^{-1}$ or $\tan^{-1}$ "as is" to give $\phi$ , since those inverse trig functions only produce angles less than or equal to $\dfrac{\pi}{2}$ .

Example. A point has cylindrical coordinates $\left(4, \dfrac{5\pi}{3}, -4\right)$ . Find its spherical coordinates.

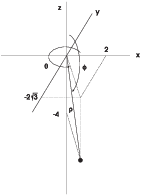
$\hbox{\epsfysize=1.75in \epsffile{spherical-coordinates-3.eps}}$

$\theta = \dfrac{5\pi}{3}$ . Since and , $\rho = 4\sqrt{2}$ by Pythagoras. Finally, the radius lies $\dfrac{\pi}{4}$ below the x-y-plane, so $\phi = \dfrac{3\pi}{4}$ .

The spherical coordinates are $\left(4\sqrt{2}, \dfrac{5\pi}{3}, \dfrac{3\pi}{4}\right)$ .

Example. Let r be the polar coordinate radius. Express r in terms of spherical coordinates.

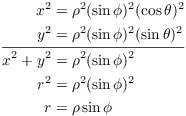
$\eqalign{ x^2 & = \rho^2 (\sin \phi)^2 (\cos \theta)^2 \cr y^2 & = \rho^2 (\sin \phi)^2 (\sin \theta)^2 \cr \noalign{\vskip2pt \hrule \vskip2pt} x^2 + y^2 & = \rho^2 (\sin \phi)^2 \cr r^2 & = \rho^2 (\sin \phi)^2 \cr r & = \rho \sin \phi \cr}$

I can take $0 \le \phi \le \pi$ (so $\sin \phi \ge 0$ ) and $\rho \ge 0$ , so I can avoid taking absolute values in the last square root step.

Example. Sketch the region in space described by the following spherical coordinate inequalities:

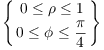
$\left\{\matrix{ 0 \le \rho \le 1 \cr \noalign{\vskip2pt} 0 \le \phi \le \dfrac{\pi}{4} \cr}\right\}$

The region lies inside the sphere of radius 1 but above the cone $\phi = \dfrac{\pi}{4}$ . Note that the latter is

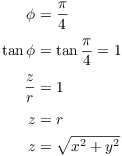
$\eqalign{ \phi & = \dfrac{\pi}{4} \cr \noalign{\vskip2pt} \tan \phi & = \tan \dfrac{\pi}{4} = 1 \cr \noalign{\vskip2pt} \dfrac{z}{r} & = 1 \cr \noalign{\vskip2pt} z & = r \cr z & = \sqrt{x^2 + y^2} \cr}$

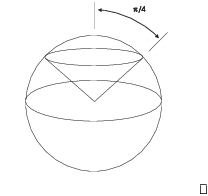
$\hbox{\epsfysize=1.75in \epsffile{spherical-coordinates-4.eps}}\quad\halmos$

The spherical conversion equations are

$x = \rho \sin \phi \cos \theta, \quad y = \rho \sin \phi \sin \theta, \quad z = \rho \cos \phi.$

They define a function $f: \real^3 \to \real^3$

$f(\rho, \theta, \phi) = (\rho \sin \phi \cos \theta, \rho \sin \phi \sin \theta, \rho \cos \phi).$

The Jacobian of f is

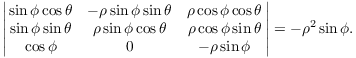
$\left|\matrix{ \sin \phi \cos \theta & -\rho \sin \phi \sin \theta & \rho \cos \phi \cos \theta \cr \sin \phi \sin \theta & \rho \sin \phi \cos \theta & \rho \cos \phi \sin \theta \cr \cos \phi & 0 & -\rho \sin \phi \cr}\right| = -\rho^2 \sin \phi.$

The absolute value is $\rho^2 \sin \phi$ . Hence, when you go from rectangular coordinates to spherical coordinates, the differentials convert by

$dx\,dy\,dz \to \rho^2 \sin \phi\,d\rho\,d\phi\,d\theta$

Therefore, in order to convert a triple integral from rectangular coordinates to spherical coordinates, you should do the following:

1. Convert the limits of integration by describing the region of integration by inequalities in spherical coordinates.

2. Convert the integrand using the spherical conversion formulas:

$x = \rho \sin \phi \cos \theta, \quad y = \rho \sin \phi \sin \theta, \quad z = \rho \cos \phi.$

$\rho^2 = x^2 + y^2 + z^2, \quad \dfrac{\sqrt{x^2 + y^2}}{z} = \tan \phi.$

3. Convert the differentials by

$dx\,dy\,dz \to \rho^2 \sin \phi\,d\rho\,d\phi\,d\theta$

Example. Let R be the interior of the sphere . Compute

$\tint_R \dfrac{\sqrt{x^2 + y^2}}{\sqrt{x^2 + y^2 + z^2}}\,dx\,dy\,dz.$

$\hbox{\epsfysize=1.75in \epsffile{spherical-coordinates-5.eps}}$

R is a sphere of radius 2 centered at the origin. The interior of the sphere is described by the inequalities

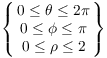
$\left\{\matrix{ 0 \le \theta \le 2 \pi \cr 0 \le \phi \le \pi \cr 0 \le \rho \le 2 \cr}\right\}$

Moreover, since $r = \rho \sin \phi$ ,

$\dfrac{\sqrt{x^2 + y^2}}{\sqrt{x^2 + y^2 + z^2}} = \dfrac{\rho \sin \phi}{\rho} = \sin \phi.$

Therefore, the integral becomes

$\int_0^{2\pi} \int_0^{\pi} \int_0^2 \rho^2 (\sin \phi)^2\,d\rho\,d\phi\,d\theta = 2 \pi \int_0^{\pi} (\sin \phi)^2 \int_0^2 \rho^2\,d\rho\,d\phi = 2 \pi \int_0^{\pi} (\sin \phi)^2 \left[ \dfrac{1}{3} \rho^3 \right]_0^2\,d\phi =$

$\dfrac{16\pi}{3} \int_0^{\pi} (\sin \phi)^2\,d\phi = \dfrac{8\pi}{3} \int_0^{\pi} (1 - \cos 2\phi)\,d\phi = \dfrac{8 \pi}{3} \left[\phi - \dfrac{1}{2} \sin 2\phi\right]_0^{\pi} = \dfrac{8 \pi^2}{3} = 26.31894 \ldots.\quad\halmos$

When should you consider converting a triple integral to spherical coordinates? Here are two rough guidelines:

(a) Consider converting to spherical coordinates when the region of integration involves graphs that "look nice" in spherical. For example, spheres and cones often produce regions that can be described by simple inequalities in spherical coordinates.

(b) Consider converting to spherical coordinates when the integrand involves terms like ( $= \rho^2$ ).

Example. Let R be the region defined by the inequalities $x^2 + y^2 + z^2 \le 4$ and $z \ge \sqrt{x^2 + y^2}$ . Compute

$\tint_R \sqrt{x^2 + y^2 + z^2}\,dx\,dy\,dz.$

is a sphere of radius 2 centered at the origin, so $x^2 + y^2 + z^2 \le 4$ refers to the interior of the sphere.

$z = \sqrt{x^2 + y^2}$ is a cone opening at a $45^{\circ}$ angle to the z-axis. Hence, $z \ge \sqrt{x^2 + y^2}$ refers to the region lying above the cone.

Together, the inequalities specify the region inside the sphere but above the cone. (It's shaped like an ice-cream cone.)

$\hbox{\epsfysize=1.75in \epsffile{spherical-coordinates-6.eps}}$

Evidently, the region "goes all the way around" the z-axis, so $0 \le \theta \le 2\pi$ . To determine the inequalities for $\rho$ , think of a searchlight beam emanating from the origin. The beam enters the ice-cream cone at the origin ( $\rho = 0$ ) and leaves the ice-cream cone through the top of the ice-cream, which is our sphere ( $\rho = 2$ ). Hence, $0 \le \rho \le 2$ .

$\phi$ is the angle measured "downward" from the z-axis. Think of an umbrella held upside-down. If you open the umbrella, through what range of angles will the ribs sweep as they pass through the region? Since the cone makes a $45^{\circ}$ ( $= \dfrac{\pi}{4}$ ) angle with the z-axis, it follows that $0 \le \phi \le \dfrac{\pi}{4}$ .

The inequalities in spherical coordinates which describe the region are

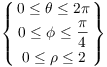
$\left\{\matrix{ 0 \le \theta \le 2 \pi \cr \noalign{\vskip2pt} 0 \le \phi \le \dfrac{\pi}{4} \cr \noalign{\vskip2pt} 0 \le \rho \le 2 \cr}\right\}$

Finally, since $\sqrt{x^2 + y^2 + z^2} = \rho$ , the integral is

$\int \int \int_R^{} \sqrt{x^2 + y^2 + z^2}\,dx\,dy\,dz = \int_0^{2\pi} \int_0^{\pi/4} \int_0^2 \rho^3 \sin \phi\,d\rho\,d\phi\,d\theta = 2 \pi \int_0^{\pi/4} \sin \phi \left[\dfrac{1}{4} \rho^4\right]_0^2\,d\phi =$

$8 \pi \int_0^{\pi/4} \sin \phi\,d\phi = 8 \pi \left[-\cos \phi \right]_0^{\pi/4} = 8 \pi \left(1 - \dfrac{\sqrt{2}}{2}\right) = 7.36120 \ldots.\quad\halmos$

Contact information

Bruce Ikenaga's Home Page