Stokes' theorem relates the integral of a vector field around the
boundary ![]() of a surface to a vector surface integral
over the surface.
of a surface to a vector surface integral
over the surface.
By the boundary of a surface, I mean its "edge" --- like the edge of the bowl below. (A surface need not have a boundary; for example, the boundary of a sphere is empty.)
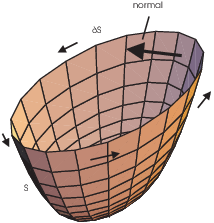
To state Stokes' theorem, I'll assume that a normal to the surface has been chosen at each point in a "smooth" way. Having done this, the boundary must be traversed in a way consistent with the choice of normal. Imagine walking along the surface near the boundary with your arms out so that your body points in the direction of the chosen normal. You should traverse the boundary in such a way that your right arm points "outside" the surface.
Now if ![]() is a 3-dimensional vector field, Stokes'
theorem says
is a 3-dimensional vector field, Stokes'
theorem says
![]()
As usual, a careful statement would include technical conditions on
the field ![]() (for instance, that it have continuous
second partial derivatives) and the surface S (for instance, that it
should be piecewise smooth).
(for instance, that it have continuous
second partial derivatives) and the surface S (for instance, that it
should be piecewise smooth).
Terminology. The line integral of a field ![]() around a closed curve is sometimes referred
to as the circulation of
around a closed curve is sometimes referred
to as the circulation of ![]() . You will often see this written as
. You will often see this written as
![]()
The "o" on the integral sign merely means that the integral
is being taken around a closed curve.![]()
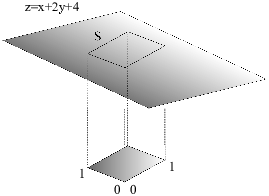
Example. Let S be the part of the plane ![]() lying above the square
lying above the square
![]()
Compute the integral of ![]() counterclockwise around the boundary of S, viewed from above.
counterclockwise around the boundary of S, viewed from above.
The boundary of the region consists of 4 segements, so doing the line integral directly would be tedious. Instead, I'll use Stokes' Theorem.
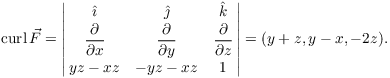
The normal vector to the plane is
![]()
Hence,
![]()
So
![]()
![]()
Example. Compute the integral of ![]() around the boundary
of the surface
around the boundary
of the surface ![]() ,
, ![]() , counterclockwise
as viewed from above. Compute the integral directly, and by using
Stokes' theorem.
, counterclockwise
as viewed from above. Compute the integral directly, and by using
Stokes' theorem.

The boundary of the region is ![]() . I can
parametrize it by
. I can
parametrize it by
![]()
Note that the boundary is traversed counterclockwise (as viewed from above).
The velocity vector for the curve is
![]()
The vector field is
![]()
Hence,
![]()
The integral around the boundary is
![]()
Next, I'll compute the circulation using Stokes' theorem. The orientation of the boundary is consistent with the upward normal for the surface. A normal is given by
![]()
The z component is positive, so this is the upward normal. (If the formula had given the downward normal, I would have multiplied the vector by -1.)
Next,
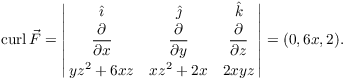
So
![]()
The integral is an x-y integral, so I integrate over the projection
of the surface into the x-y plane. The projection is the disk ![]() . I convert to polar; the disk is
. I convert to polar; the disk is
![]()
The integrand becomes
![]()
Stokes' theorem says that the circulation is
![]()
This agrees with the direct computation.![]()
Example. Compute the circulation of ![]() around the curve of
intersection of the plane
around the curve of
intersection of the plane ![]() and the hyperboloid
and the hyperboloid ![]() , where the curve is traversed in a
direction consistent with a surface normal having positive x
component.
, where the curve is traversed in a
direction consistent with a surface normal having positive x
component.
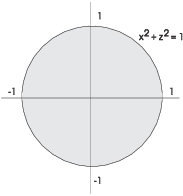
Set ![]() in
in ![]() . I obtain
. I obtain ![]() . Thus, the projection of the curve into the x-z
plane is a circle of radius 1. (Make a note of this, because I will
use it later!) To compute the line integral directly, I could use the
parametrization
. Thus, the projection of the curve into the x-z
plane is a circle of radius 1. (Make a note of this, because I will
use it later!) To compute the line integral directly, I could use the
parametrization
![]()
If you do the computation, you discover that you need to integrate
![]() . This is not too bad ...
. This is not too bad ...
Instead, I will use Stokes' theorem. Note that
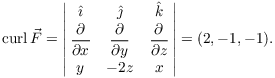
This looks fairly simple. What about the surface normal?
Your first thought might be to parametrize the hyperboloid ![]() . But Stokes' theorem allows you to use
any surface which has the given curve as its boundary.
Obviously, you should pick the simplest surface with this property,
and in this case, it is
. But Stokes' theorem allows you to use
any surface which has the given curve as its boundary.
Obviously, you should pick the simplest surface with this property,
and in this case, it is ![]() . That is, the surface is the part
of
. That is, the surface is the part
of ![]() which satisfies
which satisfies ![]() .
.
You know that if the surface is ![]() , the normal
is
, the normal
is
![]()
By swapping the variables, it follows that if the surface has the
form ![]() , the normal is
, the normal is
![]()
Now apply this formula to ![]() . I get
. I get ![]() , but the x component is negative. So
multiply the vector by -1: I get the normal
, but the x component is negative. So
multiply the vector by -1: I get the normal ![]() .
.
Hence,
![]()
What about the limits of integration? Well, I had the surface ![]() in
in ![]() form. So I should integrate
over the projection into the x-z plane. But the projection is just
the disk
form. So I should integrate
over the projection into the x-z plane. But the projection is just
the disk ![]() .
.
Therefore, Stokes' theorem gives
![]()
Example. Let S be the union of all the faces of the cube
![]()
Let ![]() . Compute the flux
of
. Compute the flux
of ![]() out through S.
out through S.
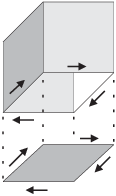
S is made up of 5 faces. While the faces are very simple surface ---
for example, the top is ![]() for
for ![]() and
and ![]() --- I'd rather not do five
surface integrals, even if they are easy.
--- I'd rather not do five
surface integrals, even if they are easy.
What about Stokes' theorem? Well, Stokes says that the flux of ![]() is equal to the circulation of
is equal to the circulation of ![]() around the boundary. The boundary is the bottom
square edge, traversed counterclockwise as viewed from above. To
compute the line integral of
around the boundary. The boundary is the bottom
square edge, traversed counterclockwise as viewed from above. To
compute the line integral of ![]() around the
boundary, I'd need to parametrize each segment, then compute the
integral along each segment.
around the
boundary, I'd need to parametrize each segment, then compute the
integral along each segment.
Four line integrals still sounds like too much ...
I'll use the "cap trick": The circulation of ![]() equals the flux of
equals the flux of ![]() through
any surface having the bottom square edge as its boundary.
Instead of using the original surface S, I'll use the (missing)
bottom face of the cube!
through
any surface having the bottom square edge as its boundary.
Instead of using the original surface S, I'll use the (missing)
bottom face of the cube!
First,
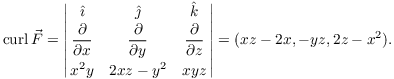
The bottom face is ![]() for
for ![]() and
and ![]() . I need the upward normal; it
is
. I need the upward normal; it
is ![]() . So
. So
![]()
The flux of ![]() is
is
![]()
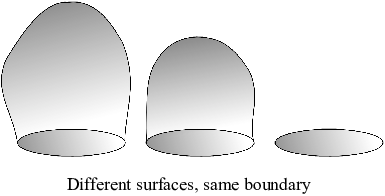
The idea used in the last example is worth highlighting:
Stokes' Theorem allows you to compute the line integral around the
boundary of a surface by computing the flux of ![]() through any surface with the same boundary.
through any surface with the same boundary.
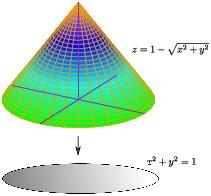
Example. Let
![]()
Let S be the part of the cone ![]() lying
above the x-y-plane. Compute
lying
above the x-y-plane. Compute
![]()
The boundary of S is traversed counterclockwise as viewed from above.
The boundary of the cone is the same as the boundary of the surface T
consisting of the disk ![]() .
.
Therefore,
![]()
I have
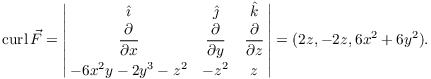
I will do the double integral in polar. The region inside the disk is
![]()
The normal vector is ![]() , so
, so
![]()
Hence, the integral is
![]()
Copyright 2018 by Bruce Ikenaga