Surface Area

I'll consider the problem of finding the area of part of a surface in $\real^3$ :

$x = f(u, v), \quad y = g(u, v), \quad z = h(u, v).$

Here is a heuristic motivation for the formula.

In our discussion of the tangent plane to a surface, we found a normal vector by taking two vectors in the tangent plane and taking their cross product. We considered a small piece of the surface near the point of tangency. A small piece will be nearly flat, and will look like the parallelogram depicted below (exaggerated so you can see it):

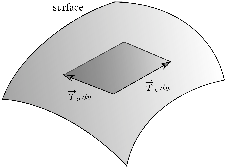
$\hbox{\epsfysize=1.5in \epsffile{surface-area-1.eps}}$

The sides of the parallelogram are determined by the tangent vectors $\bvec{T}_u$ and $\bvec{T}_v$ , scaled up the the parameter increments and . The area of the parallelogram should be the length of the cross product:

$\|\bvec{T}_v\,du \times \bvec{T}_v\,dv\| = \|\bvec{T}_v \times \bvec{T}_v\|\,du\,dv.$

To get the area of the part of the surface corresponding to the region R in the u-v plane, integrate to add up the areas of the parallelograms:

$\dint_R \|\vec{T}_u \times \vec{T}_v\|\,du\,dv.$

As a special case, consider a surface given as the graph of a function. A normal vector is given by

$\vec{N} = \left(\pder z x, \pder z y, -1\right).$

Hence,

$\|\vec{N}\| = \sqrt{\left(\pder z x\right)^2 + \left(\pder z y\right)^2 + 1}.$

In this case, the area of the surface is

$\dint_R \sqrt{\left(\pder z x\right)^2 + \left(\pder z y\right)^2 + 1}\,dx\,dy.$

Example. Find the area of the part of the surface which lies inside the cylinder .

$\pder z x = 2 y, \quad \pder z y = 2 x, \quad\hbox{so}\quad \|\vec{N}\| = \sqrt{4 y^2 + 4 x^2 + 1}.$

The region of integration is the interior of the circle :

$\left\{\matrix{ -3 \le x \le 3 \cr -\sqrt{9 - x^2} \le y \le \sqrt{9 - x^2} \cr}\right\}$

I'll convert to polar. The region becomes

$\left\{\matrix{ 0 \le \theta \le 2 \pi \cr 0 \le r \le 3 \cr}\right\}$

The integrand is

$\|\vec{N}\| = \sqrt{4 r^2 + 1}.$

The area is

$\int_0^3 \int_0^{2 \pi} \sqrt{4 r^2 + 1}r\,d\theta\,dr = 2 \pi \int_0^3 \sqrt{4 r^2 + 1} r\,dr = 2 \pi\left[\dfrac{1}{12} (4 r^2 + 1)^{3/2}\right]_0^3 = \dfrac{\pi}{6} (37^{3/2} - 1) = 117.31870 \ldots.\quad\halmos$

Example. Find the area of the surface

$x = v \cos u, \quad y = v \sin u, \quad z = v, \quad 0 \le u \le 2 \pi, \quad 0 \le v \le 2.$

$\vec{T}_u = (-v \sin u, v \cos u, 0), \quad \vec{T}_v = (\cos u, \sin u, 1),$

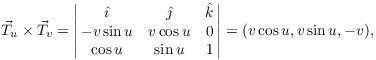
$\vec{T}_u \times \vec{T}_v = \left|\matrix{\ihat & \jhat & \khat \cr -v \sin u & v \cos u & 0 \cr \cos u & \sin u & 1 \cr}\right| = (v \cos u, v \sin u, -v),$

$\|\vec{T}_u \times \vec{T}_v\| = \sqrt{v^2 (\cos u)^2 + v^2 (\sin u)^2 + v^2} = \sqrt{2} v.$

The area of the surface is

$\int_0^2 \int_0^{2 \pi} \sqrt{2} v\,du\,dv = 2 \pi \sqrt{2} \int_0^2 v\,dv = 2 \pi \sqrt{2} \left[\dfrac{1}{2} v^2\right]_0^2 = 4 \pi \sqrt{2} = 17.77153 \ldots.\quad\halmos$

Example. (a) Find the area of the sphere by representing the top hemisphere as the graph of a function.

(b) Find the area of the sphere using the parametrization

$x = a \cos u \cos v, \quad y = a \cos u \sin v, \quad z = a \sin u, \quad -\dfrac{\pi}{2} \le u \le \dfrac{\pi}{2}, \quad 0 \le v \le 2 \pi.$

(a) The top hemisphere is

$z = \sqrt{a^2 - x^2 - y^2}.$

Thus,

$\vec{N} = \left(-\dfrac{x}{\sqrt{a^2 - x^2 - y^2}}, -\dfrac{y}{\sqrt{a^2 - x^2 - y^2}}, -1\right),$

$\|\vec{N}\| = \left(\dfrac{x^2}{a^2 - x^2 - y^2} + \dfrac{y^2}{a^2 - x^2 - y^2} + 1\right)^{1/2} = \left(\dfrac{a^2}{a^2 - x^2 - y^2}\right)^{1/2} = \dfrac{a}{\sqrt{a^2 - x^2 - y^2}}.$

The region of integration is the interior of the circle :

$\matrix{-a \le x \le a \cr -\sqrt{a^2 - x^2} \le y \le \sqrt{a^2 - x^2} \cr}$

I'll convert to polar. The region is

$\matrix{0 \le \theta \le 2 \pi \cr 0 \le r \le a \cr}$

Likewise,

$\|\vec{N}\| = \dfrac{a}{\sqrt{a^2 - r^2}}.$

I need to double the area for the top hemisphere to get the area of the whole sphere:

$2\int_0^a \int_0^{2 \pi} \dfrac{a}{\sqrt{a^2 - r^2}}r\,d\theta\,dr = 4 \pi \int_0^a \dfrac{a r}{\sqrt{a^2 - r^2}}\,dr = 4 \pi a \left[-\sqrt{a^2 - r^2}\right]_0^a = 4 \pi a^2.\quad\halmos$

(b)

$\vec{T}_u = (-a \sin u \cos v, -a \sin u \sin v, a \cos u), \quad \vec{T}_v = (-a \cos u \sin v, a \cos u \cos v, 0),$

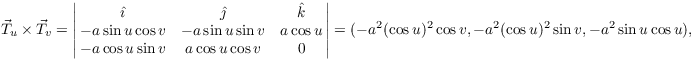
$\vec{T}_u \times \vec{T}_v = \left|\matrix{\ihat & \jhat & \khat \cr -a \sin u \cos v & -a \sin u \sin v & a \cos u \cr -a \cos u \sin v & a \cos u \cos v & 0 \cr}\right| = (-a^2 (\cos u)^2 \cos v, -a^2 (\cos u)^2 \sin v, -a^2 \sin u \cos u),$

$\|\vec{T}_u \times \vec{T}_v\| = \sqrt{a^4 (\cos u)^4 (\cos v)^2 + a^4 (\cos u)^4 (\sin v)^2 + a^4 (\sin u)^2 (\cos u)^2} = a^2 \cos u.$

The area is

$\int_{-\pi/2}^{\pi/2} \int_0^{2 \pi} a^2 \cos u\,dv\,du = 2 \pi a^2 \int_{-\pi/2}^{\pi/2} \cos u\,du = 2 \pi a^2 \left[\sin u\right]_{-\pi/2}^{\pi/2} = 4 \pi a^2. \quad\halmos$

Contact information

Bruce Ikenaga's Home Page