Tangent Vectors, Normal Vectors, and Curvature

If $\vec{f}(t) = (x(t), y(t), z(t))$ is a curve, the osculating plane is the plane determined by the velocity and acceleration vectors at a point.

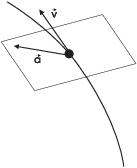
$$\hbox{\epsfysize=1.5 in \epsffile{tangent-normal-curvature-1.eps}}$$

Suppose the point on the curve is $\vec{f}(t_0)$ . Then a point $(x,y,z)$ lies in the osculating plane exactly when the following vectors determine a parallelepiped of volume 0:

$$(x, y, z) - \vec{f}(t_0), \quad \vec{f}'(t_0), \quad \vec{f}''(t_0)$$

That is,

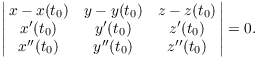
$$\left|\matrix{x - x(t_0) & y - y(t_0) & z - z(t_0) \cr x'(t_0) & y'(t_0) & z'(t_0) \cr x''(t_0) & y''(t_0) & z''(t_0) \cr}\right| = 0.$$

Example. Find the osculating plane to

$$\vec{f}(t) = (\cos t, \sin t, t) \quad\hbox{at}\quad t = \dfrac{\pi}{2}.$$

The point is $\vec{f}\left(\dfrac{\pi}{2}\right) = \left(0, 1, \dfrac{\pi}{2}\right)$ . Compute the velocity and acceleration:

$$\vec{f}'(t) = (-\sin t, \cos t, 1), \quad \vec{f}''(t) = (-\cos t, -\sin t, 0).$$

Plug in $\dfrac{\pi}{2}$ :

$$\vec{f}'\left(\dfrac{\pi}{2}\right) = (-1, 0, 1), \quad \vec{f}''\left(\dfrac{\pi}{2}\right) = (0, -1, 0).$$

The osculating plane is

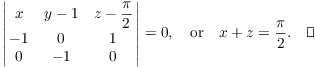
$$\left|\matrix{ x & y - 1 & z - \dfrac{\pi}{2} \cr \noalign{\vskip2pt} -1 & 0 & 1 \cr 0 & -1 & 0 \cr}\right| = 0, \quad\hbox{or}\quad x + z = \dfrac{\pi}{2}.\quad\halmos$$

The velocity vector $\vec{f}'(t)$ is tangent to the curve $\vec{f}(t)$ . If I divide the velocity vector by its length, I get a unit vector tangent to the curve. Thus, the unit tangent vector is

$$\vec T(t) = \dfrac{\vec{f}'(t)}{|\vec{f}'(t)|}.$$

I want to find a way of measuring how much a curve is curved. A reasonable way to do this is to measure the rate at which the unit tangent vector changes.

$$\hbox{\epsfysize=2 in \epsffile{tangent-normal-curvature-2.eps}}$$

When a curve is gently curved as in the top figure, the unit tangent only changes a little as you move along the curve. When a curve is sharply curved as in the bottom figure, the unit tangent changes a lot as you move along the curve.

One other thing: The "curviness" of a road should not depend on the speed of the cars which traverse it. Curviness is intrinsic to the road. The curve parameter t has to do with the rate that a hypothetical particle traces out the curve. The arc length s depends only on the path of the particle, i.e. the curve itself. Therefore, I should consider the rate of change of the unit tangent with respect to arc length.

Let s denote arc length measured along the curve from some fixed point on the curve. That is,

$$s = \int_{t_0}^t \|\vec{f}'(u)\|\,du.$$

This gives s as a function of the parameter t. For any reasonable curve, arc length measured from $t_0$ increases as you move along the curve. Since an increasing function is injective (one-to-one), it is invertible. Therefore, I can solve for t in terms of s. Then I can plug the result into the curve equations to express $\vec{f}(t) = (x(t), y(t), z(t))$ in terms of s. The result is called the arc length parametrization of the curve.

Here are some properties of the arc length parametrization:

Proposition. (a) $\der s t = \|\vec{f}'(t)\|$ .

(b) $\der {\vec{f}} s = \vec T(t)$ .

Proof. (a) Differentiate both sides of this equation with respect to t:

$$s = \int_{t_0}^t \|\vec{f}'(u)\|\,du.$$

By the Fundamental Theorem of Calculus,

$$\der s t = \|\vec{f}'(t)\|.$$

This property says that the rate of change of arc length is equal to the speed of the curve.

(b)

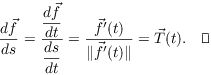
$$\der {\vec{f}} s = \dfrac{\der {\vec{f}} t}{\der s t} = \dfrac{\vec{f}'(t)}{\|\vec{f}'(t)\|} = \vec T(t).\quad\halmos$$

Example. Find the arc length parametrization of $\vec{f}(t) = \left(\dfrac{2}{9}t^{9/2}, \dfrac{1}{3}t^3\right)$ .

I'll measure arc length along the curve from $\vec{f}(0)$ . I want to use t as the parameter, so I'll switch to u as the dummy integration variable. Thus, $\vec{f}(u) = \left(\dfrac{2}{9}u^{9/2}, \dfrac{1}{3}u^3\right)$ .

Now $\vec{f}'(u) = (u^{7/2}, u^2)$ , so

$$s = \int_0^t \sqrt{u^7 + u^4}\,du = \int_0^t u^2\sqrt{u^3 + 1}\,du = \dfrac{2}{9}\left((t^3 + 1)^{3/2} - 1\right).$$

Solve for t in terms of s:

$$t = \root 3 \of {\left(\dfrac{9}{2} s + 1\right)^{2/3} - 1}.$$

Therefore, the arc length parametrization of the curve is

$$\vec{f}(s) = \left(\dfrac{2}{9} \left[\left(\dfrac{9}{2}s + 1\right)^{2/3} - 1\right]^{3/2}, \dfrac{1}{3} \left[\left(\dfrac{9}{2} s + 1\right)^{2/3} - 1\right]\right).\quad\halmos$$

Definition. The curvature vector is $\der {\vec T} s$ . It measures how much a curve is curved by finding the rate of change of the unit tangent with respect to arc length.

The curvature is the length of the curvature vector:

$$\kappa = \left\|\der {\vec T} s\right\|.$$

Remark. Some people define curvature in a way that allows it to be positive or negative. Since I've defined curvature as the length of a vector, my definition requires that it be positive.

Proposition. (a) $\der {\vec T} s$ is perpendicular to $\vec T$ .

(b) $\der {\vec T} s$ lies in the plane determined by the velocity and acceleration vectors --- i.e. the osculating plane.

Proof. (a) Differentiate $\vec T \cdot \vec T = 1$ with respect to s:

$$2 \vec T\cdot \der {\vec T} s = 0, \quad\hbox{or}\quad \vec T\cdot \der {\vec T} s = 0.$$

Therefore, $\der {\vec T} s$ is perpendicular to $\vec T$ .

(b) By the Chain Rule and the Product Rule,

$$\der {\vec T} s = \der {} s \left(\der {\vec{f}} s\right) = \der {} s \left(\der {\vec{f}} t\cdot \der t s \right) = \der {} s \left(\der {\vec{f}} t\right) \der t s + \der {\vec{f}} t \dfrac{d^2 t}{ds^2} = \dfrac{d^2\vec{f}}{dt^2} \left(\der t s\right)^2 + \der {\vec{f}} t \dfrac{d^2 t}{ds^2}.$$

The last expression is a linear combination of the velocity and acceleration vectors. Therefore, $\der {\vec T} s$ lies in the plane determined by the velocity and acceleration vectors.

Definition. The unit normal is given by

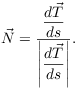
$$\vec N = \dfrac{\der {\vec T} s}{\left|\der {\vec T} s\right|}.$$

Thus, the unit vector is a unit vector perpendicular to the unit tangent $\vec T$ . Moreover, the curvature vector has length equal to the curvature and direction given by the unit normal:

$$\der {\vec T} s = \kappa \vec N.$$

Next, I want to obtain some formulas for the curvature. I'll need a couple of lemmas.

Lemma.

$$\der {} t \|\vec{f}\,'(t)\| = \dfrac{\vec{f}\,'(t)\cdot \vec{f}\,''(t)}{\|\vec{f}\,'(t)\|}.$$

Proof. Since $\|\vec{v}\|^2 = \vec{v}\cdot \vec{v}$ ,

$$\|\vec{f}\,'(t)\|^2 = \vec{f}\,'(t) \cdot \vec{f}\,'(t).$$

Differentiate with respect to t:

$$2\|\vec{f}\,'(t)\|\der {} t \|\vec{f}\,'(t)\| = \vec{f}\,'(t) \cdot \vec{f}\,''(t) + \vec{f}\,''(t) \cdot \vec{f}\,'(t) = 2\vec{f}\,'(t) \cdot \vec{f}\,''(t),$$

$$\|\vec{f}\,'(t)\|\der {} t \|\vec{f}\,'(t)\| = \vec{f}\,'(t) \cdot \vec{f}\,''(t),$$

$$\der {} t \|\vec{f}\,'(t)\| = \dfrac{\vec{f}\,'(t) \cdot \vec{f}\,''(t)}{\|\vec{f}\,'(t)\|}.\quad\halmos$$

Lemma.

$$(\vec{a} \times \vec{b}) \cdot (\vec{a}\times \vec{b}) = (\vec{a} \cdot \vec{a})(\vec{b} \cdot \vec{b}) - (\vec{a} \cdot \vec{b})^2.$$

Proof.

$$(\vec{a} \times \vec{b}) \cdot (\vec{a} \times \vec{b}) = \|\vec{a} \times \vec{b}\|^2 = \|\vec{a}\|^2 \|\vec{b}\|^2 (\sin \theta)^2 = \|\vec{a}\|^2 \|\vec{b}\|^2 - \|\vec{a}\|^2 \|\vec{b}\|^2 (\cos \theta)^2 = (\vec{a} \cdot \vec{a})(\vec{b} \cdot \vec{b}) - (\vec{a} \cdot \vec{b})^2.\quad\halmos$$

In the next result, primes will denote differentiation with respect to t (not s). Thus, $\vec{f}\,' = \der {\vec{f}} t$ .

Theorem.

$$\kappa = \dfrac{\|\vec{f}\,'\times \vec{f}\,''\|}{\|\vec{f}\,'\|^{3/2}}.$$

Proof.

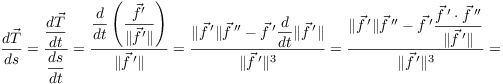
$$\der {\vec{T}} s = \dfrac{\der {\vec{T}} t}{\der s t} = \dfrac{\der {} t \left(\dfrac{\vec{f}'}{\|\vec{f}'\|}\right)} {\|\vec{f}\,'\|} = \dfrac{\|\vec{f}\,'\|\vec{f}\,'' - \vec{f}\,' \der {} t \|\vec{f}\,'\|} {\|\vec{f}\,'\|^3} = \dfrac{\|\vec{f}\,'\|\vec{f}\,'' - \vec{f}\,' \dfrac{\vec{f}\,'\cdot \vec{f}\,''} {\|\vec{f}\,'\|}}{\|\vec{f}\,'\|^3} =$$

$$\dfrac{\|\vec{f}\,'\|^2\vec{f}\,'' - (\vec{f}\,'\cdot \vec{f}\,'')\vec{f}\,'} {\|\vec{f}\,'\|^4} = \dfrac{(\vec{f}\,'\cdot \vec{f}\,')\vec{f}\,'' - (\vec{f}\,'\cdot \vec{f}\,'')\vec{f}\,'} {\|\vec{f}\,'\|^4}.$$

Now $\kappa$ is the length of $\der {\vec{T}} s$ , so by multiplying out the dot products,

$$\kappa^2 = \der {\vec{T}} s\cdot \der {\vec{T}} s = \dfrac{1}{\|\vec{f}\,'\|^8} \left((\vec{f}\,'\cdot \vec{f}\,')^2 (\vec{f}\,''\cdot \vec{f}\,'') - 2(\vec{f}\,'\cdot \vec{f}\,') (\vec{f}\,'\cdot \vec{f}\,'')^2 + (\vec{f}\,'\cdot \vec{f}\,'')^2 (\vec{f}\,'\cdot \vec{f}\,')\right) =$$

$$\dfrac{1}{\|\vec{f}\,'\|^8} \left((\vec{f}\,'\cdot \vec{f}\,')^2 (\vec{f}\,''\cdot \vec{f}\,'') - (\vec{f}\,'\cdot \vec{f}\,') (\vec{f}\,'\cdot \vec{f}\,'')^2\right) = \dfrac{1}{\|\vec{f}\,'\|^6} \left((\vec{f}\,'\cdot \vec{f}\,') (\vec{f}\,''\cdot \vec{f}\,'') - (\vec{f}\,'\cdot \vec{f}\,'')^2\right) =$$

$$\dfrac{1}{\|\vec{f}\,'\|^6} \left((\vec{f}\,'\times \vec{f}\,'') \cdot (\vec{f}\,'\times \vec{f}\,'')\right) = \dfrac{\|\vec{f}\,'\times \vec{f}\,''\|^2} {\|\vec{f}\,'\|^6}.$$

For the next to the last equality, I used the vector identity from the preceding lemma. Finally, take the square root of both sides:

$$\kappa = \dfrac{\|\vec{f}\,'\times \vec{f}\,''\|} {\|\vec{f}\,'\|^3}.\quad\halmos$$

Example. Find the curvature of the helix

$$\vec{f}(t) = (\cos t, \sin t, t) \quad\hbox{at}\quad t = \dfrac{\pi}{2}.$$

$$\vec{f}\,'(t) = (-\sin t, \cos t, 1) \quad\hbox{and}\quad \vec{f}\,''(t) = (-\cos t, -\sin t, 0).$$

Hence,

$$\vec{f}\,'\left(\dfrac{\pi}{2}\right) = (-1, 0, 1) \quad\hbox{and}\quad \vec{f}\,''\left(\dfrac{\pi}{2}\right) = (0, -1, 0).$$

Then

$$\left\|\vec{f}\,'\left(\dfrac{\pi}{2}\right)\right\| = \sqrt{2},$$

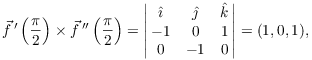
$$\vec{f}\,'\left(\dfrac{\pi}{2}\right)\times \vec{f}\,''\left(\dfrac{\pi}{2}\right) = \left|\matrix{ \ihat & \jhat & \khat \cr -1 & 0 & 1 \cr 0 & -1 & 0 \cr}\right| = (1, 0, 1),$$

$$\left\|\vec{f}\,'\left(\dfrac{\pi}{2}\right)\times \vec{f}\,''\left(\dfrac{\pi}{2}\right)\right\| = \sqrt{2}.$$

The curvature is

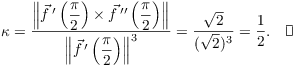
$$\kappa = \dfrac{\left\|\vec{f}\,'\left(\dfrac{\pi}{2}\right) \times \vec{f}\,''\left(\dfrac{\pi}{2}\right)\right\|} {\left\|\vec{f}\,'\left(\dfrac{\pi}{2}\right)\right\|^3} = \dfrac{\sqrt{2}}{(\sqrt{2})^3} = \dfrac{1}{2}.\quad\halmos$$

Next, I'll obtain formulas for the curvature of a curve in the x-y-plane.

Theorem. (a) If $\vec{f}(t) = (x(t), y(t))$ is a curve in the x-y-plane, then

$$\kappa = \dfrac{|x' y'' - x'' y'|}{(x')^2 + (y')^2)^{3/2}}.$$

(b) If $y = f(x)$ is a curve in the x-y-plane, then

$$\kappa = \dfrac{|f''(x)|}{[1 + (f'(x))^2]^{3/2}}.$$

Proof. (a) Regard $\vec{f}$ as a curve in 3 dimensions by writing $\vec{f}(t) = (x(t), y(t), 0)$ . Then

$$\vec{f}\,' = (x', y', 0) \quad\hbox{and}\quad \vec{f}\,'' = (x'', y'', 0).$$

So

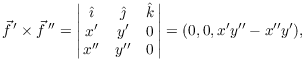
$$\vec{f}\,' \times \vec{f}\,'' = \left|\matrix{ \ihat & \jhat & \khat \cr x' & y' & 0 \cr x'' & y'' & 0 \cr}\right| = (0, 0, x' y'' - x'' y'),$$

$$\|\vec{f}\,' \times \vec{f}\,''\| = |x' y'' - x'' y'|.$$

Since $\|\vec{f}\,'\| = \sqrt{(x')^2 + (y')^2}$ , I have

$$\kappa = \dfrac{\|\vec{f}\,'\times \vec{f}\,''\|} {\|\vec{f}\,'\|^3} = \dfrac{|x' y'' - x'' y'|}{(x')^2 + (y')^2)^{3/2}}.$$

(b) I may parametrize $y = f(x)$ by setting $x = t$ , $y = f(t)$ . Then

$$x' = 1, \quad x'' = 0, \quad y' = f'(t), \quad y'' = f''(t).$$

Plugging these into the formula from the first part of the theorem, I get

$$\kappa = \dfrac{|x' y'' - x''y'|}{(x')^2 + (y')^2)^{3/2}} = \dfrac{|f''(t)|}{[1 + (f'(t))^2]^{3/2}} = \dfrac{|f''(x)|}{[1 + (f'(x))^2]^{3/2}}.\quad\halmos$$

Example. Find the curvature of

$$x = (\cos t)^3, \quad y = (\sin t)^3.$$

I have

$$x' = -3(\cos t)^2\sin t, \quad y' = 3(\sin t)^2\cos t,$$

$$x'' = -3(\cos t)^3 + 6(\cos t)(\sin t)^2, \quad y'' = -3(\sin t)^3 + 6(\sin t)(\cos t)^2.$$

Hence,

$$x' y'' - x'' y' = \left(-3(\cos t)^2\sin t\right) \left(-3(\sin t)^3 + 6(\sin t)(\cos t)^2\right) - \left(-3(\cos t)^3 + 6(\cos t)(\sin t)^2\right) \left(3(\sin t)^2\cos t\right) =$$

$$9(\sin t)^4(\cos t)^2 - 18(\sin t)^2(\cos t)^4 + 9(\sin t)^2(\cos t)^4 - 18(\sin t)^4(\cos t)^2 =$$

$$-9(\sin t)^4(\cos t)^2 - 9(\sin t)^2(\cos t)^4 = -9(\sin t)^2(\cos t)^2\left((\sin t)^2 + (\cos t)^2\right) = -9(\sin t)^2(\cos t)^2.$$

Also,

$$(x')^2 + (y')^2 = 9(\cos t)^4(\sin t)^2 + 9(\sin t)^4(\cos t)^2 = 9(\sin t)^2(\cos t)^2\left((\cos t)^2 + (\sin t)^2\right) = 9(\sin t)^2(\cos t)^2.$$

The curvature is

$$\kappa = \dfrac{|-9(\sin t)^2(\cos t)^2|}{(9(\sin t)^2(\cos t)^2)^{3/2}} = \dfrac{1}{3|\sin t \cos t|}.\quad\halmos$$

Example. Find the curvature of $y = x^2$ at the point $(2, 4)$ .

$$y' = 2 x, \quad y'' = 2.$$

Thus, $y'(2) = 4$ and $y''(2) = 2$ .

The curvature is

$$\kappa = \dfrac{|2|}{(1 + 4^2)^{3/2}} = \dfrac{2}{17^{3/2}}.\quad\halmos$$

In computing the unit normal, a reasonable strategy is to compute the unit tangent $\vec{T}(t)$ . The unit normal has the same direction as $\der {\vec{T}} s$ , but

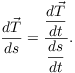
$$\der {\vec{T}} s = \dfrac{\der {\vec{T}} t}{\der s t}.$$

The stuff on the bottom is a number; therefore, the unit normal has the same direction as $\der {\vec{T}} t$ . So I can compute $\der {\vec{T}} t$ and then divide it by its length; since it has the right direction and right length, it must be the unit normal.

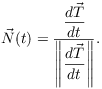
$$\vec{N}(t) = \dfrac{\der {\vec{T}} t}{\left\|\der {\vec{T}} t\right\|}.$$

Example. Find the unit tangent and unit normal to the helix $\vec{f}(t) = (\cos t, \sin t, t)$ .

$$\vec{f}\,'(t) = (-\sin t, \cos t, 1) \quad\hbox{and}\quad \|\vec{f}\,'(t)\| = \sqrt{(-\sin t)^2 + (\cos t)^2 + 1} = \sqrt{2}.$$

Hence,

$$\vec{T}(t) = \dfrac{1}{\sqrt{2}}(-\sin t, \cos t, 1).$$

Next,

$$\der {\vec{T}} t = \dfrac{1}{\sqrt{2}}(-\cos t, -\sin t, 0) \quad\hbox{and}\quad \left\|\der {\vec{T}} t\right\| = \dfrac{1}{\sqrt{2}}\sqrt{(-\cos t)^2 + (-\sin t)^2 + 0} = \dfrac{1}{\sqrt{2}}.$$

Therefore,

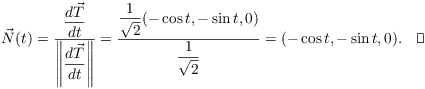
$$\vec{N}(t) = \dfrac{\der {\vec{T}} t}{\left\|\der {\vec{T}} t\right\|} = \dfrac{\dfrac{1}{\sqrt{2}}(-\cos t, -\sin t, 0)}{\dfrac{1}{\sqrt{2}}} = (-\cos t, -\sin t, 0).\quad\halmos$$

For curves in the plane, it's often easy to see what the unit normal is by inspection. The unit normal points in the direction in which the curve is curving:

$$\hbox{\epsfysize=1.75 in \epsffile{tangent-normal-curvature-3.eps}}$$

Once you know a tangent vector $(a, b)$ , there are two obvious vectors which are perpendicular to $(a, b)$ :

$$(b, -a) \quad\hbox{and}\quad (-b, a).$$

Just pick the one that points in the direction in which the curve is curving, divide by its length, and you have the unit normal.

Example. Find the unit tangent and unit normal to the curve $\vec{f}(t) = (t^2, t^3)$ .

$$\vec{f}\,'(t) = (2 t, 3 t^2) \quad\hbox{and}\quad \|\vec{f}\,'(t)\| = \sqrt{4 t^2 + 9 t^4}.$$

Hence,

$$\vec{T}(t) = \dfrac{1}{\sqrt{9 t^4 + 4 t^2}}(2 t, 3 t^2).$$

Remember that the unit normal must be perpendicular to the unit tangent! Ignore the factor of $\dfrac{1}{\sqrt{9 t^4 + 4 t^2}}$ which is a number and doesn't affect the tangent's direction --- the direction of $\vec{T}(t)$ is given by $(2 t, 3 t^2)$ . There are two obvious vectors in the plane perpendicular to it, namely

$$(3 t^2, -2 t) \quad\hbox{and}\quad (-3 t^2, 2 t).$$

Here's a picture of the curve:

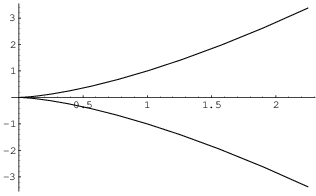
$$\hbox{\epsfysize=1.75 in \epsffile{tangent-normal-curvature-4.eps}}$$

You can see that the normal vector should always point to the left, so its x-coordinate must be negative. Therefore, $(-3 t^2, 2 t)$ points in the direction of the normal. Now

$$\|(-3 t^2, 2 t)\| = \sqrt{9 t^4 + 4 t^2}, \quad\hbox{so}\quad \vec{N}(t) = \dfrac{1}{\sqrt{9 t^4 + 4 t^2}}(-3 t^2, 2 t). \quad\halmos$$

The binormal $\vec{B}$ is the cross product of the unit tangent and unit normal:

$$\vec{B} = \vec{T} \times \vec{N}.$$

Since the cross product of unit vectors is a unit vector, the binormal is a unit vector which is perpendicular to the unit tangent and unit normal.

Example. Find the binormal vector for the helix $\vec{f}(t) = (\cos t, \sin t, t)$ .

I computed the unit tangent and unit normal in an earlier example:

$$\vec{T}(t) = \dfrac{1}{\sqrt{2}}(-\sin t, \cos t, 1),$$

$$\vec{N}(t) = (-\cos t, -\sin t, 0).$$

Therefore,

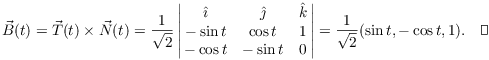
$$\vec{B}(t) = \vec{T}(t) \times \vec{N}(t) = \dfrac{1}{\sqrt{2}}\left|\matrix{\ihat & \jhat & \khat \cr -\sin t & \cos t & 1 \cr -\cos t & -\sin t & 0 \cr}\right| = \dfrac{1}{\sqrt{2}}(\sin t, -\cos t, 1).\quad\halmos$$

The radius of curvature is defined to be $R = \dfrac{1}{\kappa}$ . The osculating circle at a point on a curve is the circle of radius R, tangent to the curve at the point, whose center lies R units along the unit normal $\vec{N}$ from the point. The circle lies in the osculating plane. The parametric equations for the osculating circle at $t = t_0$ are

$$(x, y, z) - \vec{f}(t_0) - R \vec{N} = R \vec{T} \cos u + R \vec{N} \sin u.$$

Example. Find the osculating circle to the helix

$$\vec{f}(t) = (\cos t, \sin t, t) \quad\hbox{at}\quad t = \dfrac{\pi}{2}.$$

First, $\vec{f}\left(\dfrac{\pi}{2}\right) = \left(0, 1, \dfrac{\pi}{2}\right)$ .

The unit tangent, unit normal, and curvature are

$$\vec{T}\left(\dfrac{\pi}{2}\right) = \dfrac{1}{\sqrt{2}}(-1, 0, 1), \quad \vec{N}\left(\dfrac{\pi}{2}\right) = (0, -1, 0), \quad R = 2.$$

The osculating circle is

$$(x, y, z) - \left(0, 1, \dfrac{\pi}{2}\right) - 2 (0, -1, 0) = 2 \cdot \dfrac{1}{\sqrt{2}} (-1, 0, 1)\cos u + 2 \cdot (0, -1, 0)\sin u.$$

Simplifying and solving for x, y, and z, I get

$$x = -\sqrt{2} \cos u, \quad y = -2 \sin u - 1, \quad z = \dfrac{\pi}{2} + \sqrt{2} \cos u.\quad\halmos$$

Example. Find the osculating circle to $y = x^2$ at $(2, 4)$ .

Parametrizing the curve by $x = t$ , $y = t^2$ , I have

$$\vec{f}(t) = (t, t^2), \quad \vec{f}\,'(t) = (1, 2 t).$$

Thus, $\vec{f}\,'(2) = (1, 4)$ , so

$$\vec{T}(2) = \dfrac{1}{\sqrt{17}}(1, 4) \quad\hbox{and}\quad \vec{N}(2) = \dfrac{1}{\sqrt{17}}(-4, 1).$$

Next,

$$\kappa = \dfrac{y''(2)}{(1 + (y'(2))^2)^{3/2}} = \dfrac{2}{17^{3/2}}, \quad\hbox{so}\quad R = \dfrac{17^{3/2}}{2}.$$

The center is $\dfrac{17^{3/2}}{2}$ units from $(2, 4)$ in the direction given by $\vec{N}$ :

$$(2, 4) + \dfrac{17^{3/2}}{2} \cdot \dfrac{1}{\sqrt{17}}(-4, 1) = \left(-32, \dfrac{25}{2}\right).$$

Therefore, the circle is

$$x = -32 + \dfrac{17^{3/2}}{2} \cos u, \quad y = \dfrac{25}{2} + \dfrac{17^{3/2}}{2} \sin u.\quad\halmos$$

Contact information

Bruce Ikenaga's Home Page

Copyright 2019 by Bruce Ikenaga