Triple Integrals

If R is a region in $\real^3$ and is a continuous function, the triple integral of f over R can be computed as an iterated integral. In this regard, triple integrals aren't conceptually more difficult than double integrals, though their computation will usually be more involved.

The process of setting up a triple integral in routine situations goes something like this, assuming that the region R is "reasonable". I'll label the coordinate axes p, q, and r, and you can relabel them with whatever combination of "x", "y", and "z" is appropriate in your problem. Suppose that you can project R into the p-q plane and get a region S that you can describe by inequalities like these:

$\left\{\matrix{ a \le p \le b \cr g(p) \le q \le h(p) \cr}\right\}$

These will give the limits for p and q. For r, imagine passing through the region R in the r-direction:

$\hbox{\epsfysize=1.75in \epsffile{triple-integrals-1.eps}}$

If you "enter" the region at and "leave" the region at , then and give the limit on r. Thus, the region is

$\left\{\matrix{ a \le p \le b \cr g(p) \le q \le h(p) \cr j(p, q) \le r \le k(p, q) \cr}\right\}$

And

$\tint_R f(p, q, r)\,dp\,dq\,dr = \int_a^b \int_{g(p)}^{h(p)} \int_{j(p, q)}^{k(p, q)} f(p, q, r)\,dr\,dq\,dp.$

Example. Consider the region in the first octant cut off by the plane

$\hbox{\epsfysize=1.75in \epsffile{triple-integrals-2.eps}}$

Describe the region by inequalities by:

(a) Projecting it into the x-y-plane.

(b) Projecting it into the y-z-plane.

(a)

$\hbox{\epsfysize=1.75in \epsffile{triple-integrals-3.eps}}$

$\left\{\matrix{ 0 \le x \le 6 \cr \noalign{\vskip2pt} 0 \le y \le \dfrac{1}{3} (6 - x) \cr \noalign{\vskip2pt} 0 \le z \le \dfrac{1}{2} (6 - x - 3 y) \cr}\right\}\quad\halmos$

(b)

$\hbox{\epsfysize=1.75in \epsffile{triple-integrals-4.eps}}$

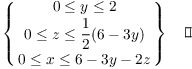
$\left\{\matrix{ 0 \le y \le 2 \cr \noalign{\vskip2pt} 0 \le z \le \dfrac{1}{2} (6 - 3 y) \cr \noalign{\vskip2pt} 0 \le x \le 6 - 3 y - 2 z \cr}\right\}\quad\halmos$

(c)

$\hbox{\epsfysize=1.75in \epsffile{triple-integrals-5.eps}}$

$\left\{\matrix{ 0 \le x \le 6 \cr \noalign{\vskip2pt} 0 \le z \le \dfrac{1}{2} (6 - x) \cr \noalign{\vskip2pt} 0 \le y \le \dfrac{1}{3} (6 - x - 2 z) \cr}\right\}\quad\halmos$

By analogy with double integrals,

$\tint_R dx\,dy\,dz = (\hbox{volume of R}).$

Example. Without computing any antiderivatives, compute

$\int_{-3}^5 \int_0^2 \int_1^7 dx\,dy\,dz.$

$\hbox{\epsfysize=1.75in \epsffile{triple-integrals-6.eps}}$

The integral represents the volume of a box with sides of lengths 6, 2, and 8. Hence,

$\int_{-3}^5 \int_0^2 \int_1^7 dx\,dy\,dz = 6 \cdot 2 \cdot 8 = 96.\quad\halmos$

Example. Without computing any antiderivatives, compute

$\int_{0}^2 \int_0^{\sqrt{4 - x^2}} \int_0^{\sqrt{4 - x^2 - y^2}} dz\,dy\,dx.$

Note that $z = \sqrt{4 - x^2 - y^2}$ gives

This is a sphere of radius 2 centered at the origin. Look at the limits of integration:

$\left\{\matrix{ 0 \le x \le 2 \cr 0 \le y \le \sqrt{4 - x^2} \cr 0 \le z \le \sqrt{4 - x^2 - y^2} \cr}\right\}$

The x and y-limits describe a quarter circle of radius 2. The limits on z describe the top half of the sphere. Since $\dfrac{1}{2} \cdot \dfrac{1}{4} = \dfrac{1}{8}$ , the integral represents the volume of one-eighth of a sphere of radius 2.

$\hbox{\epsfysize=1.75in \epsffile{triple-integrals-7.eps}}$

The volume of a sphere of radius r is $\dfrac{4}{3} \pi r^3$ . Hence,

$\int_{0}^2 \int_0^{\sqrt{4 - x^2}} \int_0^{\sqrt{4 - x^2 - y^2}} dz\,dy\,dx = \dfrac{1}{8} \cdot \dfrac{4}{3} \pi \cdot 2^3 = \dfrac{4}{3} \pi.\quad\halmos$

Example. Compute $\displaystyle \tint_R (6 x y + 12)\,dx\,dy\,dz$ , where R is the unit cube

$\left\{\matrix{ 0 \le x \le 1 \cr 0 \le y \le 1 \cr 0 \le z \le 1 \cr}\right\}$

$\tint_R (6 x y + 12)\,dx\,dy\,dz = \int_0^1 \int_0^1 \int_0^1 (x + 2y + 4z)\,dx\,dy\,dz = \dfrac{27}{2}.\quad\halmos$

Example. Compute

$\int_{-2}^2 \int_0^y \int_0^{x^2} (6 y + 2 z)\,dz\,dx\,dy.$

$\int_{-2}^2 \int_0^y \int_0^{x^2} (6 y + 2 z)\,dz\,dx\,dy = \int_{-2}^2 \int_0^y \left[6 y z + z^2\right]_0^{x^2}\,dx\,dy = \int_{-2}^2 \int_0^y (6 x^2 y + x^4)\,dx\,dy =$

$\int_{-2}^2 \int_0^y (6 x^2 y + x^4)\,dx\,dy = \int_{-2}^2 \left[2 x^3 y + \dfrac{1}{5} x^5\right]_0^y\,dy = \int_{-2}^2 \left(2 y^4 + \dfrac{1}{5} y^5\right)\,dy =$

$\left[\dfrac{2}{5} y^5 + \dfrac{1}{30} y^6\right]_{-2}^2 = \dfrac{128}{5}.\quad\halmos$

Example. Let R be the region bounded by the planes

$x = 0, \quad y = 0, \quad x + y = 1, \quad z = 0, \quad\hbox{and}\quad z = 1.$

Compute $\displaystyle \tint_R (x - 2y)\,dx\,dy\,dz$ .

$\hbox{\epsfysize=1.75in \epsffile{triple-integrals-8.eps}}$

The region is

$\left\{\matrix{ 0 \le x \le 1 \cr 0 \le y 1 - x \cr 0 \le z \le 1 \cr}\right\}$

$\tint_R (x - 2y)\,dx\,dy\,dz = \int_0^1 \int_0^{1 - x} \int_0^1 (x - 2 y)\,dz\,dy\,dx = \int_0^1 \int_0^{1 - x} \left[(x - 2 y) z\right]_0^1\,dy\,dx =$

$\int_0^1 \int_0^{1 - x} (x - 2 y)\,dy\,dx = \int_0^1 \left[x y - y^2\right]_0^{1 - x}\,dx = \int_0^1 \left(x (1 - x) - (1 - x)^2\right)\,dx =$

$\int_0^1 \left(x - x^2 - 1 + 2 x - x^2\right)\,dx = \int_0^1 \left(-2 x^2 + 3 x - 1\right)\,dx = \left[-\dfrac{2}{3} x^3 + \dfrac{3}{2} x^2 - x\right]_0^1 = -\dfrac{1}{6}.\quad\halmos$

Contact information

Bruce Ikenaga's Home Page