Velocity and Acceleration

A function $f: \real \to \real^n$ can be thought of as a curve in $\real^n$ . Write the curve in parametric form

$$f(t) = (f_1(t), f_2(t), \ldots f_n(t)).$$

Think of the parameter t as time and the curve as being traced out by a moving object, so that the object is at the position $f(t)$ at time t.

With this interpretation:

(a) $f'(t)$ is the velocity vector of the object. It points in the direction that the object is travelling at time t. Its length is the speed of the object at time t.

(b) $f''(t)$ is the acceleration vector of the object. It represents the direction and magnitude of the change of the velocity vector at time t.

Example. Find the velocity and acceleration vectors at $t = 3$ for the curve with position function

$$f(t) = \left(e^{2 t} + t, \dfrac{1}{t + 1}, (2 t - 5)^2\right).$$

The velocity is the derivative of the position:

$$v(t) = f'(t) = \left(2 e^{2 t} + 1, -\dfrac{1}{(t + 1)^2}, 4(2 t - 5)\right).$$

The acceleration is the derivative of the velocity:

$$a(t) = f''(t) = \left(4 e^{2 t}, \dfrac{2}{(t + 1)^3}, 8\right).$$

Setting $t = 3$ gives

$$v(3) = \left(2 e^6 + 1, -\dfrac{1}{16}, 4\right) \quad\hbox{and}\quad a(3) = \left(4 e^6, \dfrac{1}{32}, 8\right).\quad\halmos$$

Example. The position of an evil lime jello at time t is

$$f(t) = (2 t^3 - 3 t^2 + 5, 7 t + 1, t^2 + 3 t).$$

Find its velocity vector and its speed at $t = 2$ .

The velocity is the derivative of the position:

$$v(t) = f'(t) = (6 t^2 - 6 t, 7, 2 t + 3).$$

The velocity at $t = 2$ is

$$v(2) = f'(2) = (12, 7, 7).$$

The speed is the length of the velocity vector:

$$\|v(2)\| = \sqrt{12^2 + 7^2 + 7^2} = \sqrt{242}.\quad\halmos$$

Example. A cheeseburger moves on a circular helix given by

$$f(t) = (\cos 2 t, \sin 2 t, 3 t).$$

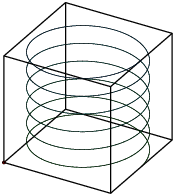
$$\hbox{\epsfysize=1.75in \epsffile{velocity-and-acceleration-1.eps}}$$

Show that it moves with constant speed.

The velocity vector is

$$v(t) = f'(t) = (-2 \sin 2 t, 2 \cos 2 t, 3).$$

The speed is the length of the velocity vector, which is

$$\|v(t)\| = \sqrt{4 (\sin 2t)^2 + 4 (\cos 2 t)^2 + 9} = \sqrt{13}.$$

Thus, the cheeseburger moves with constant speed.

Example. Prove that if a curve $f(t)$ has constant length, then its velocity and position vectors are always perpendicular.

I'll use the fact that the square of the length of a vector equals the dot product of the vector with itself:

$$\|v\|^2 = v \cdot v.$$

Suppose $\|f(t)\| = r$ , where r is a constant. Then use the identity above, differentiate, and apply the Product Rule for dot products:

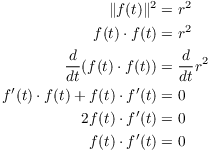
$$\eqalign{ \|f(t)\|^2 & = r^2 \cr f(t) \cdot f(t) & = r^2 \cr \der {} t (f(t) \cdot f(t)) & = \der {} t r^2 \cr f'(t) \cdot f(t) + f(t) \cdot f'(t) & = 0 \cr 2 f(t) \cdot f'(t) & = 0 \cr f(t) \cdot f'(t) & = 0 \cr}$$

Since $f(t)$ and $f'(t)$ have dot product 0, they are perpendicular.

Note: To say that $f(t)$ has constant length r means that a point on the curve stays a constant distance r from the origin. Thus, it must be moving on the sphere of radius r centered at the origin.

Since $v(t) = f'(t)$ , you can integrate to find the position function from the velocity:

$$f(t) = \int v(t)\,dt.$$

Likewise, since $a(t) = v'(t)$ , you can integrate to find the velocity from the acceleration:

$$v(t) = \int a(t)\,dt.$$

Antiderivatives are only determined up to an arbitrary constant. But you may be able to determine the arbitrary constant if you are given initial conditions.

Example. The acceleration vector for a bacon quiche is

$$a(t) = \left(30 t, 6\right).$$

Find the position function $f(t)$ , if $v(1) = (21, 7)$ and $f(1) = (9, 8)$ .

$$v(t) = \int a(t)\,dt = \int \left(30 t, 6\right)\,dt = \left(15 t^2, 6 t\right) + (c_1, c_2).$$

Now $v(1) = (21, 7)$ , so

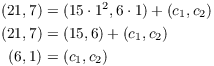
$$\eqalign{ (21, 7) & = (15 \cdot 1^2, 6 \cdot 1) + (c_1, c_2) \cr (21, 7) & = (15, 6) + (c_1, c_2) \cr (6, 1) & = (c_1, c_2) \cr}$$

Hence,

$$v(t) = \left(15 t^2, 6 t\right) + (6, 1) = \left(15 t^2 + 6, 6 t + 1\right).$$

Next,

$$f(t) = \int v(t)\,dt = \int \left(15 t^2 + 6, 6 t + 1\right)\,dt = \left(5 t^3 + 6 t, 3 t^2 + t\right) + (d_1, d_2).$$

Now $f(1) = (9, 8)$ , so

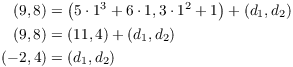
$$\eqalign{ (9, 8) & = \left(5 \cdot 1^3 + 6 \cdot 1, 3 \cdot 1^2 + 1\right) + (d_1, d_2) \cr (9, 8) & = (11, 4) + (d_1, d_2) \cr (-2, 4) & = (d_1, d_2) \cr}$$

Hence,

$$f(t) = \left(5 t^3 + 6 t, 3 t^2 + t\right) + (-2, 4) = \left(5 t^3 + 6 t - 2, 3 t^2 + t + 4\right).\quad\halmos$$

Contact information

Bruce Ikenaga's Home Page

Copyright 2018 by Bruce Ikenaga