Bases for Vector Spaces

A set is independent if, roughly speaking, there is no redundancy in the set: You can't "build" any vector in the set as a linear combination of the others. A set spans if you can "build everything" in the vector space as linear combinations of vectors in the set. Putting these two ideas together, a basis is an independent spanning set: A set with no redundancy out of which you can "build everything".

Definition. Let V be an F-vector space. A subset ${\cal B}$ of V is a basis if it is linearly independent and spans V.

Definition. Let F be a field. The standard basis for $F^n$ consists of the n vectors

$$(1, 0, 0, \ldots 0),\ (0, 1, 0, \ldots 0),\ (0, 0, 1, \ldots 0), \ldots (0, 0, 0, \ldots 1).$$

Thus, the $k^{\rm th}$ standard basis vector has a "1" in the $k^{\rm th}$ slot and zeros elsewhere.

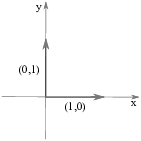
The standard basis vectors in $\real^2$ are $(1, 0)$ and $(0, 1)$ . They can be pictured as arrows of length 1 pointing along the positive x-axis and positive y-axis.

$$\hbox{\epsfysize=1.25in \epsffile{bases-1.eps}}$$

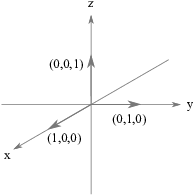
The standard basis vectors in $\real^3$ are $(1, 0, 0)$ , $(0, 1, 0)$ , and $(0, 0, 1)$ . They can be pictured as arrows of length 1 pointing along the positive x-axis, the positive y-axis, and the positive z-axis.

$$\hbox{\epsfysize=1.75in \epsffile{bases-2.eps}}$$

Since we're calling this a "basis", we'd better check that the name is justified!

Proposition. The standard basis is a basis for $F^n$ .

Proof. First, we show that the standard basis spans $F^n$ . Let $(a_1, a_2, a_3, \ldots a_n) \in F^n$ . I must write this vector as a linear combination of the standard basis vectors. It's easy:

$$\matrix{ & & a_1 \cdot (1, 0, 0, \ldots 0) \cr & & a_2 \cdot (0, 1, 0, \ldots 0) \cr & & a_3 \cdot (0, 0, 1, \ldots 0) \cr & & \vdots \cr + & & a_n \cdot (0, 0, 0, \ldots 1) \cr \noalign{\vskip2pt \hrule \vskip2pt} & & (a_1, a_2, a_3, \ldots a_n) \cr}$$

For independence, suppose

$$a_1 (1, 0, 0, \ldots, 0) + a_2 (0, 1, 0, \ldots, 0) + a_3 (0, 0, 1, \ldots 0) + \cdots a_n (0, 0, 0, \ldots 1) = (0, 0, 0, \ldots 0).$$

The computation we did to prove that the set spans shows that the left side is just $(a_1, a_2, a_3, \ldots a_n)$ , so

$$(a_1, a_2, a_3, \ldots a_n) = (0, 0, 0, \ldots 0).$$

This implies that $a_1 = a_2 = a_3 = \cdots = a_n = 0$ , so the set is independent.

Aside from giving us an example of a basis for $F^n$ , this result shows that at least one basis for $F^n$ has n elements. We will show later that every basis for $F^n$ has n elements.

Example. Prove that the following set is a basis for $\real^3$ over $\real$ :

$$\left\{\left[\matrix{1 \cr 1 \cr 0 \cr}\right], \left[\matrix{0 \cr 1 \cr 1 \cr}\right], \left[\matrix{1 \cr 0 \cr 1 \cr}\right]\right\}$$

Make a matrix with the vectors as columns and row reduce:

$$A = \left[\matrix{1 & 0 & 1 \cr 1 & 1 & 0 \cr 0 & 1 & 1 \cr}\right] \quad \to \quad \left[\matrix{1 & 0 & 0 \cr 0 & 1 & 0 \cr 0 & 0 & 1 \cr}\right]$$

Since A row reduces to the identity, it is invertible,and there are a number of conditions which are equivalent to A being invertible.

First, since A is invertible the following system has a unique solution for every $(a, b, c)$ :

$$\left[\matrix{1 & 0 & 1 \cr 1 & 1 & 0 \cr 0 & 1 & 1 \cr}\right] \left[\matrix{x \cr y \cr z \cr}\right] = \left[\matrix{a \cr b \cr c \cr}\right].$$

But this matrix equation can be written as

$$x \cdot \left[\matrix{1 \cr 1 \cr 0 \cr}\right] + y \cdot \left[\matrix{0 \cr 1 \cr 1 \cr}\right] + z \cdot \left[\matrix{1 \cr 0 \cr 1 \cr}\right] = \left[\matrix{a \cr b \cr c \cr}\right].$$

In other words, any vector $(a, b, c) \in \real^3$ can be written as a linear combination of the given vectors. This proves that the given vectors span $\real^3$ .

Second, since A is invertible, the following system has only $x = 0$ , $y = 0$ , $z = 0$ as a solution:

$$\left[\matrix{1 & 0 & 1 \cr 1 & 1 & 0 \cr 0 & 1 & 1 \cr}\right] \left[\matrix{x \cr y \cr z \cr}\right] = \left[\matrix{0 \cr 0 \cr 0 \cr}\right].$$

This matrix equation can be written as

$$x \cdot \left[\matrix{1 \cr 1 \cr 0 \cr}\right] + y \cdot \left[\matrix{0 \cr 1 \cr 1 \cr}\right] + z \cdot \left[\matrix{1 \cr 0 \cr 1 \cr}\right] = \left[\matrix{0 \cr 0 \cr 0 \cr}\right].$$

Since the only solution is $x = 0$ , $y = 0$ , $z = 0$ , the vectors are independent.

Hence, the given set of vectors is a basis for $\real^3$ .

We'll generalize the computations we did in the last example.

Proposition. Let F be a field. $\{v_1, v_2, \ldots, v_n\}$ is a basis for $F^n$ if and only if

$$A = \left[\matrix{\uparrow & \uparrow & & \uparrow \cr v_1 & v_2 & \cdots & v_n \cr \downarrow & \downarrow & & \downarrow \cr}\right] \quad\hbox{is invertible}.\quad\halmos$$

Remark. By earlier results on invertibility, this is equivalent to the following conditions:

1. A row reduces to the identity.

2. $\det A \ne 0$ .

3. The system $A x = 0$ has only $x = (x_1, x_2, \ldots x_n) = (0, 0, \ldots 0)$ as a solution.

4. For every vector $b = (b_1, b_2, \ldots b_n) \in F^n$ , the system $A x = b$ has a unique solution.

Thus, if you have n vectors in $F^n$ , this gives you several ways of checking whether or not the set is a basis.

Proof. Suppose $\{v_1, v_2, \ldots, v_n\}$ is a basis for $F^n$ . Let

$$A = \left[\matrix{\uparrow & \uparrow & & \uparrow \cr v_1 & v_2 & \cdots & v_n \cr \downarrow & \downarrow & & \downarrow \cr}\right].$$

Consider the system

$$\left[\matrix{\uparrow & \uparrow & & \uparrow \cr v_1 & v_2 & \cdots & v_n \cr \downarrow & \downarrow & & \downarrow \cr}\right] \left[\matrix{x_1 \cr x_2 \cr \vdots \cr x_n \cr}\right] = \left[\matrix{0 \cr 0 \cr \vdots \cr 0 \cr}\right].$$

Doing the matrix multiplication on the left and writing the result as a vector equation, we have

$$x_1 v_1 + x_2 v_2 + \cdots + x_n v_n = (0, 0, \ldots 0).$$

Since $\{v_1, v_2, \ldots, v_n\}$ is independent, I have $x_1 = x_2 = \cdots = x_n = 0$ . This shows that the system above has only the zero vector as a solution. An earlier result on invertibility shows that A must be invertible.

Conversely, suppose the following matrix is invertible:

$$A = \left[\matrix{\uparrow & \uparrow & & \uparrow \cr v_1 & v_2 & \cdots & v_n \cr \downarrow & \downarrow & & \downarrow \cr}\right].$$

We will show that $\{v_1, v_2, \ldots, v_n\}$ is a basis.

For independence, suppose

$$x_1 v_1 + x_2 v_2 + \cdots + x_n v_n = (0, 0, \ldots 0).$$

Writing the left side as a matrix multiplication gives the system

$$\left[\matrix{\uparrow & \uparrow & & \uparrow \cr v_1 & v_2 & \cdots & v_n \cr \downarrow & \downarrow & & \downarrow \cr}\right] \left[\matrix{x_1 \cr x_2 \cr \vdots \cr x_n \cr}\right] = \left[\matrix{0 \cr 0 \cr \vdots \cr 0 \cr}\right].$$

Since A is invertible, the only solution to this system is $x_1 = x_2 = \cdots = x_n = 0$ . This shows that $\{v_1, v_2, \ldots, v_n\}$ is independent.

To show that $\{v_1, v_2, \ldots, v_n\}$ spans, let $(b_1, b_2, \ldots b_n) \in F^n$ . Consider the system

$$\left[\matrix{\uparrow & \uparrow & & \uparrow \cr v_1 & v_2 & \cdots & v_n \cr \downarrow & \downarrow & & \downarrow \cr}\right] \left[\matrix{x_1 \cr x_2 \cr \vdots \cr x_n \cr}\right] = \left[\matrix{b_1 \cr b_2 \cr \vdots \cr b_n \cr}\right].$$

Since A is invertible, this system has a (unique) solution $(x_1, x_2, \ldots x_n)$ . That is,

$$x_1 v_1 + x_2 v_2 + \cdots + x_n v_n = (b_1, b_2, \ldots b_n).$$

This shows that $\{v_1, v_2, \ldots, v_n\}$ spans.

Hence, $\{v_1, v_2, \ldots, v_n\}$ is a basis for $F^n$ .

A basis for V is a spanning set for V, so every vector in V can be written as a linear combination of basis elements. The next result says that such a linear combination is unique.

Proposition. Let ${\cal B}$ be a basis for a vector space V. Every $v \in V$ can be written in exactly one way as

$$v = a_1 v_1 + a_2 v_2 + \cdots + a_n v_n, \quad a_i \in F, \quad v_1, \ldots v_n \in {\cal B}.$$

Proof. Let $v \in V$ . Since ${\cal B}$ spans V, there are scalars $a_1$ , $a_2$ , ..., $a_n$ and vectors $v_1, \ldots v_n \in {\cal B}$ such that

$$v = a_1 v_1 + a_2 v_2 + \cdots + a_n v_n.$$

Suppose that there is another way to do this: There are scalars $b_1$ , $b_2$ , ..., $b_m$ and vectors $w_1, \ldots w_m \in {\cal B}$ such that

$$v = b_1 w_1 + b_2 w_2 + \cdots + b_m w_m.$$

First, note that I can assume that the same set of vectors are involved in both linear combinations --- that is, the v's and w's are the same set of vectors. For if not, I can instead use the vectors in the union

$$S = \{v_1, \ldots v_n\} \cup \{w_1, \ldots w_m\}.$$

I can rewrite both of the original linear combinations as linear combinations of vectors in S, using 0 as the coefficient of any vector which doesn't occur in a given combination. Then both linear combinations for v use the same vectors.

I'll assume this has been done and just assume that $\{v_1, v_2, \ldots v_n\}$ is the set of vectors. Thus, I have two linear combinations

$$\eqalign{ v & = a_1 v_1 + a_2 v_2 + \cdots + a_n v_n \cr v & = b_1 v_1 + b_2 v_2 + \cdots + b_n v_n \cr}$$

Then

$$a_1 v_1 + a_2 v_2 + \cdots + a_n v_n = b_1 v_1 + b_2 v_2 + \cdots + b_n v_n.$$

Hence,

$$(a_1 - b_1)v_1 + (a_2 - b_2)v_2 + \cdots + (a_n - b_n)v_n = 0.$$

Since $\{v_1, v_2, \ldots, v_n\}$ is independent,

$$a_1 - b_1 = 0, \quad a_2 - b_2 = 0, \ldots, a_n - b_n = 0.$$

Therefore,

$$a_1 = b_1, \quad a_2 = b_2, \ldots, a_n = b_n.$$

That is, the two linear combinations were actually the same. This proves that there's only one way to write v as a linear combination of vectors in ${\cal B}$ .

I want to show that two bases for a vector space must have the same number of elements. I need some preliminary results, which are important in their own right.

Lemma. If A is an $m \times n$ matrix with $m < n$ , the system $A x = 0$ has nontrivial solutions.

Proof. Write

$$A = \left[\matrix{ a_{1 1} & a_{1 2} & \cdots & a_{1 n} \cr a_{2 1} & a_{2 2} & \cdots & a_{2 n} \cr \vdots & \vdots & & \vdots \cr a_{m 1} & a_{m 2} & \cdots & a_{m n} \cr}\right].$$

The condition $m < n$ means that the following system has more variables than equations:

$$\left[\matrix{ a_{1 1} & a_{1 2} & \cdots & a_{1 n} \cr a_{2 1} & a_{2 2} & \cdots & a_{2 n} \cr \vdots & \vdots & & \vdots \cr a_{m 1} & a_{m 2} & \cdots & a_{m n} \cr}\right] \left[\matrix{x_1 \cr x_2 \cr \vdots \cr x_n \cr}\right] = \left[\matrix{0 \cr 0 \cr \vdots \cr 0 \cr}\right].$$

If A row reduces to a row reduced echelon matrix R, then R can have at most m leading coefficients. Therefore, some of the variables $x_1$ , $x_2$ , ..., $x_n$ will be free variables (parameters); if I assign nonzero values to the free variables (e.g. by setting all of them equal to 1), the resulting solution will be nontrivial.

Theorem. Let $\{v_1, v_2, \ldots, v_n\}$ be a basis for a vector space V over a field F.

(a) Any subset of V with more than n elements is dependent.

(b) Any subset of V with fewer than n elements cannot span.

Proof. (a) Suppose $\{w_1, w_2, \ldots, w_m\}$ is a subset of V, and that $m > n$ . I want to show that $\{w_1, w_2, \ldots, w_m\}$ is dependent.

Write each w as a linear combination of the v's:

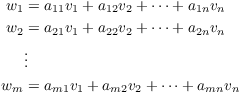
$$\eqalign{ w_1 &= a_{1 1} v_1 + a_{1 2} v_2 + \cdots + a_{1 n} v_n \cr w_2 &= a_{2 1} v_1 + a_{2 2} v_2 + \cdots + a_{2 n} v_n \cr & \vdots \cr w_m &= a_{m 1} v_1 + a_{m 2} v_2 + \cdots + a_{m n} v_n \cr}$$

This can be represented as the following matrix equation:

$$\left[\matrix{ \uparrow & \uparrow & & \uparrow \cr w_1 & w_2 & \cdots & w_m \cr \downarrow & \downarrow & & \downarrow \cr}\right] = \left[\matrix{ \uparrow & \uparrow & & \uparrow \cr v_1 & v_2 & \cdots & v_n \cr \downarrow & \downarrow & & \downarrow \cr}\right] \left[\matrix{ a_{1 1} & a_{2 1} & \cdots & a_{m 1} \cr a_{1 2} & a_{2 2} & \cdots & a_{m 2} \cr \vdots & \vdots & & \vdots \cr a_{1 n} & a_{2 n} & \cdots & a_{m n} \cr}\right].$$

Since $m > n$ , the matrix of a's has more columns than rows. Therefore, the following system has a nontrivial solution $x_1 = b_1$ , $x_2 = b_2$ , ... $x_m = b_m$ :

$$\left[\matrix{ a_{1 1} & a_{2 1} & \cdots & a_{m 1} \cr a_{1 2} & a_{2 2} & \cdots & a_{m 2} \cr \vdots & \vdots & & \vdots \cr a_{1 n} & a_{2 n} & \cdots & a_{m n} \cr}\right] \left[\matrix{x_1 \cr x_2 \cr \vdots \cr x_m \cr}\right] = \left[\matrix{0 \cr 0 \cr \vdots \cr 0 \cr}\right].$$

That is, not all the b's are 0, but

$$\left[\matrix{ a_{1 1} & a_{2 1} & \cdots & a_{m 1} \cr a_{1 2} & a_{2 2} & \cdots & a_{m 2} \cr \vdots & \vdots & & \vdots \cr a_{1 n} & a_{2 n} & \cdots & a_{m n} \cr}\right] \left[\matrix{b_1 \cr b_2 \cr \vdots \cr b_m \cr}\right] = \left[\matrix{0 \cr 0 \cr \vdots \cr 0 \cr}\right].$$

But then

$$\left[\matrix{ \uparrow & \uparrow & & \uparrow \cr w_1 & w_2 & \cdots & w_m \cr \downarrow & \downarrow & & \downarrow \cr}\right] \left[\matrix{b_1 \cr b_2 \cr \vdots \cr b_m \cr}\right] = \left[\matrix{ \uparrow & \uparrow & & \uparrow \cr v_1 & v_2 & \cdots & v_n \cr \downarrow & \downarrow & & \downarrow \cr}\right] \left[\matrix{ a_{1 1} & a_{2 1} & \cdots & a_{m 1} \cr a_{1 2} & a_{2 2} & \cdots & a_{m 2} \cr \vdots & \vdots & & \vdots \cr a_{1 n} & a_{2 n} & \cdots & a_{m n} \cr}\right] \left[\matrix{b_1 \cr b_2 \cr \vdots \cr b_m \cr}\right].$$

Therefore,

$$\left[\matrix{ \uparrow & \uparrow & & \uparrow \cr w_1 & w_2 & \cdots & w_m \cr \downarrow & \downarrow & & \downarrow \cr}\right] \left[\matrix{b_1 \cr b_2 \cr \vdots \cr b_m \cr}\right] = \left[\matrix{0 \cr 0 \cr \vdots \cr 0 \cr}\right].$$

In equation form,

$$b_1 w_1 + b_2 w_2 + \cdots + b_m w_m = 0.$$

This is a nontrivial linear combination of the w's which adds up to 0, so the w's are dependent.

(b) Suppose that $\{w_1, w_2, \ldots, w_m\}$ is a set of vectors in V and $m < n$ . I want to show that $\{w_1, w_2, \ldots, w_m\}$ does not span V.

Suppose on the contrary that the w's span V. Then each v can be written as a linear combination of the w's:

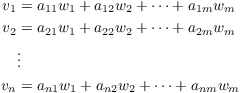
$$\eqalign{ v_1 &= a_{1 1} w_1 + a_{1 2} w_2 + \cdots + a_{1 m} w_m \cr v_2 &= a_{2 1} w_1 + a_{2 2} w_2 + \cdots + a_{2 m} w_m \cr & \vdots \cr v_n &= a_{n 1} w_1 + a_{n 2} w_2 + \cdots + a_{n m} w_m \cr}$$

In matrix form, this is

$$\left[\matrix{ \uparrow & \uparrow & & \uparrow \cr v_1 & v_2 & \cdots & v_n \cr \downarrow & \downarrow & & \downarrow \cr}\right] = \left[\matrix{ \uparrow & \uparrow & & \uparrow \cr w_1 & w_2 & \cdots & w_m \cr \downarrow & \downarrow & & \downarrow \cr}\right] \left[\matrix{ a_{1 1} & a_{2 1} & \cdots & a_{n 1} \cr a_{1 2} & a_{2 2} & \cdots & a_{n 2} \cr \vdots & \vdots & & \vdots \cr a_{1 m} & a_{2 m} & \cdots & a_{n m} \cr}\right].$$

Since $n > m$ , the coefficient matrix has more columns than rows. Hence, the following system has a nontrivial solution $x_1 = b_1$ , $x_2 = b_2$ , ... $x_n = b_n$ :

$$\left[\matrix{ a_{1 1} & a_{2 1} & \cdots & a_{n 1} \cr a_{1 2} & a_{2 2} & \cdots & a_{n 2} \cr \vdots & \vdots & & \vdots \cr a_{1 m} & a_{2 m} & \cdots & a_{n m} \cr}\right] \left[\matrix{x_1 \cr x_2 \cr \vdots \cr x_n \cr}\right] = \left[\matrix{0 \cr 0 \cr \vdots \cr 0 \cr}\right].$$

Thus,

$$\left[\matrix{ a_{1 1} & a_{2 1} & \cdots & a_{n 1} \cr a_{1 2} & a_{2 2} & \cdots & a_{n 2} \cr \vdots & \vdots & & \vdots \cr a_{1 m} & a_{2 m} & \cdots & a_{n m} \cr}\right] \left[\matrix{b_1 \cr b_2 \cr \vdots \cr b_n \cr}\right] = \left[\matrix{0 \cr 0 \cr \vdots \cr 0 \cr}\right].$$

Multiplying the v and w equation on the right by the b-vector gives

$$\left[\matrix{ \uparrow & \uparrow & & \uparrow \cr v_1 & v_2 & \cdots & v_n \cr \downarrow & \downarrow & & \downarrow \cr}\right] \left[\matrix{b_1 \cr b_2 \cr \vdots \cr b_n \cr}\right] = \left[\matrix{ \uparrow & \uparrow & & \uparrow \cr w_1 & w_2 & \cdots & w_m \cr \downarrow & \downarrow & & \downarrow \cr}\right] \left[\matrix{ a_{1 1} & a_{2 1} & \cdots & a_{n 1} \cr a_{1 2} & a_{2 2} & \cdots & a_{n 2} \cr \vdots & \vdots & & \vdots \cr a_{1 m} & a_{2 m} & \cdots & a_{n m} \cr}\right] \left[\matrix{b_1 \cr b_2 \cr \vdots \cr b_n \cr}\right].$$

Hence,

$$\left[\matrix{ \uparrow & \uparrow & & \uparrow \cr v_1 & v_2 & \cdots & v_n \cr \downarrow & \downarrow & & \downarrow \cr}\right] \left[\matrix{b_1 \cr b_2 \cr \vdots \cr b_n \cr}\right] = \left[\matrix{0 \cr 0 \cr \vdots \cr 0 \cr}\right].$$

In equation form, this is

$$b_1 v_1 + b_2 v_2 + \cdots + b_n v_n = 0.$$

Since not all the b's are 0, this is a nontrivial linear combination of the v's which adds up to 0 --- contradicting the independence of the v's.

This contradiction means that the w's can't span after all.

Corollary. Let F be a field.

(a) Any subset of $F^n$ with more than n elements is dependent.

(b) Any subset of $F^n$ with fewer than n elements cannot span.

Proof. This follows from the Theorem, and the fact that the standard basis for $F^n$ has n elements.

As an example, the following set of four vectors in $\real^3$ can't be independent:

$$\left\{\left[\matrix{1 \cr 0 \cr -1 \cr}\right], \left[\matrix{2 \cr -3 \cr 10 \cr}\right], \left[\matrix{1 \cr 1 \cr 1 \cr}\right], \left[\matrix{0 \cr 11 \cr -7 \cr}\right]\right\}$$

Likewise, the following set of two vectors can't span $\real^3$ :

$$\left\{\left[\matrix{-2 \cr 1 \cr 2 \cr}\right], \left[\matrix{3 \cr 1 \cr 5 \cr}\right]\right\}\quad\halmos$$

Corollary. If $\{v_1, \ldots, v_n\}$ is a basis for a vector space V, then every basis for V has n elements.

Proof. If $\{w_1, \ldots, w_m\}$ is another basis for V, then m can't be less than n or $\{w_1, \ldots, w_m\}$ couldn't span. Likewise, m can't be greater than n or $\{w_1, \ldots, w_m\}$ couldn't be independent. Therefore, $m = n$ .

The Corollary allows us to define the dimension of a vector space.

Definition. The number of elements in a basis for V is called the dimension of V, and is denoted $\dim V$ .

The definition makes sense, since in a finite-dimensional vector space, any two bases have the same number of elements. This is true in general; I'll state the relevant results without proof.

(a) Every vector space has a basis. The proof requires a set-theoretic result called Zorn's Lemma.

(b) Two bases for any vector space have the same cardinality. Specifically, if ${\cal B}$ and ${\cal C}$ are bases for a vector space V, there is a bijective function $f: {\cal B} \to {\cal C}$ .

Here's an example of a basis with an infinite number of elements.

Example. Let $\real[x]$ denote the $\real$ -vector space of polynomials with coefficients in $\real$ .

Show that $\{1, x, x^2, x^3, \ldots\}$ is a basis for $\real[x]$ .

First, a polynomial has the form $a_n x^n + a_{n - 1} x^{n - 1} + \cdots + a_1 x + a_0$ . This is a linear combination of elements of $\{1, x, x^2, x^3, \ldots\}$ . Hence, the set spans $\real[x]$ .

To show that the set is independent, suppose there are numbers $a_0, a_1, \ldots a_n \in \real$ such that

$$a_0 + a_1 x + \cdots + a_n x^n = 0.$$

This equation is an identity --- it's true for all $x \in \real$ . Setting $x = 0$ , I get $a_0 = 0$ . Then plugging $a_0 = 0$ back in gives

$$a_1 x + \cdots + a_n x^n = 0.$$

Since this is an identity, I can differentiate both sides to obtain

$$a_1 + 2 a_2 x + \cdots + n a_n x^{n - 1} = 0.$$

Setting $x = 0$ gives $a_1 = 0$ . Plugging $a_1 = 0$ back in gives

$$2 a_2 x + \cdots + n a_n x^{n - 1} = 0.$$

Continuing in this way, I get $a_0 = a_1 = \cdots = a_n = 0$ . Hence, the set is independent.

Therefore, $\{1, x, x^2, x^3, \ldots\}$ is a basis for $\real[x]$ .

The next result shows that, in principle, you can construct a basis by:

(a) Starting with an independent set and adding vectors.

(b) Starting with a spanning set and removing vectors.

Theorem. Let V be a finite-dimensional vector space.

(a) Any set of independent vectors is a subset of a basis for V.

(b) Any spanning set for V contains a subset which is a basis.

Part (a) means that if S is an independent set, then there is a basis T such that $S \subset T$ . (If S was a basis to begin with, then $S = T$ .) Part (b) means that if S is a spanning set, then there is a basis T such that $T \subset S$ .

I'm only proving the result in the case where V has finite dimension n, but it is true for vector spaces of any dimension.

Proof.

(a) Let $\{v_1, \ldots, v_m\}$ be independent. If this set spans V, it's a basis, and I'm done. Otherwise, there is a vector $v \in V$ which is not in the span of $\{v_1, \ldots, v_m\}$ .

I claim that $\{v, v_1, \ldots, v_m\}$ is independent. Suppose

$$a v + a_1 v_1 + \cdots + a_m v_m = 0.$$

Suppose $a \ne 0$ . Then I can write

$$v = -\dfrac{1}{a}\left(a_1 v_1 + \cdots + a_m v_m\right).$$

Since v has been expressed as a linear combination of the $v_k$ 's, it's in the span of the $v_k$ 's, contrary to assumption. Therefore, this case is ruled out.

The only other possibility is $a = 0$ . Then $a_1 v_1 + \cdots + a_m v_m = 0$ , so independence of the $v_k$ 's implies $a_1 = \cdots = a_m = 0$ . Therefore, $\{v, v_1, \ldots, v_m\}$ is independent.

I can continue adding vectors in this way until I get a set which is independent and spans --- a basis. The process must terminate, since no independent set in V can have more than n elements.

(b) Suppose $\{v_1, \ldots, v_m\}$ spans V. I want to show that some subset of $\{v_1, \ldots, v_m\}$ is a basis.

If $\{v_1, \ldots, v_m\}$ is independent, it's a basis, and I'm done. Otherwise, there is a nontrivial linear combination

$$a_1 v_1 + \cdots + a_m v_m = 0.$$

Assume without loss of generality that $a_1 \ne 0$ . Then

$$v_1 = -\dfrac{1}{a_1}\left(a_2 v_2 + \cdots + a_m v_m\right).$$

Since $v_1$ is a linear combination of the other v's, I can remove it and still have a set which spans V; that is, $V = \langle v_2, \ldots, v_m \rangle$ .

I continue throwing out vectors in this way until I reach a set which spans and is independent --- a basis. The process must terminate, because no set containing fewer than n vectors can span V.

It's possible to carry out the "adding vectors" and "removing vectors" procedures in some specific cases. The algorithms are related to those for finding bases for the row space and column space of a matrix, which I'll discuss later.

Suppose you know a basis should have n elements, and you have a set S with n elements ("the right number"). To show S is a basis, you only need to check either that it is independent or that it spans --- not both. I'll justify this statement, then show by example how you can use it. I need a preliminary result.

Proposition. Let V be a finite dimensional vector space over a field F, and let W be a subspace of V. If $\dim W = \dim V$ , then $V = W$ .

Proof. Suppose $\dim W = \dim V = n$ , but $V \ne W$ . I'll show that this leads to a contradiction.

Let $\{x_1, x_2, \ldots, x_n\}$ be a basis for W. Suppose this is not a basis for V. Since it's an independent set, the previous result shows that I can add vectors $y_1$ , $y_2$ , ... $y_m$ to make a basis for V:

$$\{x_1, x_2, \ldots, x_n, y_1, y_2, \ldots y_m\}.$$

But this is a basis for V with more than n elements, which is impossible.

Therefore, $\{x_1, x_2, \ldots, x_n\}$ is also a basis for V. Let $x \in V$ . Since $\{x_1, x_2, \ldots, x_n\}$ spans V, I can write x as a linear combination of the elements of $\{x_1, x_2, \ldots, x_n\}$ :

$$x = a_1 x_1 + a_2 x_2 + \cdots + a_n x_n, \quad a_i \in F.$$

But since $x_1$ , $x_2$ , ... $x_n$ are in W and W is a subspace, any linear combination of $x_1$ , $x_2$ , ... $x_n$ must be in W. Thus, $x \in W$ .

Since x was an arbitrary element of V, I get $V \subset W$ , so $W = V$ .

You might be thinking that this result is obvious: W and V have the same dimension, and you can't have one thing inside another, with both things having the "same size", unless the things are equal. This is intuitively what is going on here, but this kind of intuitive reasoning doesn't always work. For example, the even integers are a subset of the integers and, as infinite sets, both are of the same "order of infinity" ( cardinality). But the even integers aren't all of the integers: There are odd integers as well.

Corollary. Let S be a set of n vectors in an n-dimensional vector space V.

(a) If S is independent, then S is a basis for V.

(b) If S spans V, then S is a basis for V.

Proof. (a) Suppose S is independent. Consider W, the span of S. Then S is independent and spans W, so S is a basis for W. Since S has n elements, $\dim W = n$ . But $W \subset V$ and $\dim V = n$ . By the preceding result, $V = W$ .

Hence, S spans V, and S is a basis for V.

(b) Suppose S spans V. Suppose S is not independent. By an earlier result, I can remove some elements of S to get a set T which is a basis for V. But now I have a basis T for V with fewer than n elements (since I removed elements from S, which had n elements).

This is a contradiction, and hence S must be independent.

Example. (a) Determine whether $\{(1, 2, 1), (2, 1, 1), (2, 0, 1)\}$ is a basis for the $\integer_3$ vector space $\integer_3^3$ .

(b) Determine whether $\{(1, 1, 0), (1, 2, 2), (2, 2, 0)\}$ is a basis for the $\integer_3$ vector space $\integer_3^3$ .

(a) Form the matrix with the vectors as columns and row reduce:

$$\left[\matrix{ 1 & 2 & 2 \cr 2 & 1 & 0 \cr 1 & 1 & 1 \cr}\right] \quad \to \quad \left[\matrix{ 1 & 0 & 0 \cr 0 & 1 & 0 \cr 0 & 0 & 1 \cr}\right]$$

Since the matrix row reduces to the identity, it is invertible. Since the matrix is invertible, the vectors are independent. Since we have 3 vectors in a 3-dimensional vector space, the Corollary says that the set is a basis.

(b) Form the matrix with the vectors as columns and row reduce:

$$\left[\matrix{ 1 & 1 & 2 \cr 1 & 2 & 2 \cr 0 & 2 & 0 \cr}\right] \quad \to \quad \left[\matrix{ 1 & 0 & 2 \cr 0 & 1 & 0 \cr 0 & 0 & 0 \cr}\right]$$

The matrix did not row reduce to the identity, so it is not invertible. Since the matrix is not invertible, the vectors aren't independent. Hence, the vectors are not a basis.

Contact information

Bruce Ikenaga's Home Page

Copyright 2022 by Bruce Ikenaga