Coordinates and Change of Basis

Let V be a vector space and let ${\cal B}$ be a basis for V. Every vector $v \in V$ can be uniquely expressed as a linear combination of elements of ${\cal B}$ :

$v = a_1 v_1 + \cdots + a_n v_n, \qquad v_i \in {\cal B}, \quad a_i \in F.$

(Let me remind you of why this is true. Since a basis spans, every $v \in V$ can be written in this way. On the other hand, if $a_1 v_1 + \cdots + a_n v_n = a_1' v_1 + \cdots + a_n' v_n$ are two ways of writing a given vector, then $(a_1 - a_1')v_1 + \cdots (a_n - a_n')v_n = 0$ , and by independence , ..., --- that is, , ..., . So the representation of a vector in this way is unique.)

Consider the situation where ${\cal B}$ is a finite ordered basis --- that is, fix a numbering $v_1, \ldots, v_n$ of the elements of ${\cal B}$ . If $v = a_1 v_1 + \cdots + a_n v_n$ , the ordered list of coefficients $( a_1, \ldots, a_n)$ is uniquely associated with v. The $\{ a_i\}$ are the components of v with respect to the (ordered) basis ${\cal B}$ ; I will use the notation

$v = ( a_1, \ldots, a_n)_{\cal B}.$

It is easy to confuse a vector with the representation of the vector in terms of its components relative to a basis. This confusion arises because representation of vectors which is most familiar is that of a vector as an ordinary n-tuple in $\real^n$ :

$\real^n = \{( a_1, \ldots, a_n) \mid a_i \in \real\}.$

This amounts to identifying the elements of $\real^n$ with their representation relative to the standard basis

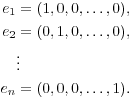
$\eqalign { e_1 &= ( 1, 0, 0, \ldots, 0),\cr e_2 &= ( 0, 1, 0, \ldots, 0),\cr & \vdots \cr e_n &= ( 0, 0, 0, \ldots, 1).\cr }$

Example. (a) Show that

${\cal B} = \left\{\left[\matrix{1 \cr 0 \cr 1 \cr}\right], \left[\matrix{2 \cr -1 \cr 1 \cr}\right], \left[\matrix{3 \cr 1 \cr 0 \cr}\right]\right\}$

is a basis for $\real^3$ .

These are three vectors in $\real^3$ , which has dimension 3. Hence, it suffices to check that they're independent. Form the matrix with the elements of ${\cal B}$ as its rows and row reduce:

$\left[\matrix{1 & 0 & 1 \cr 2 & -1 & 1 \cr 3 & 1 & 0 \cr}\right] \quad \rightarrow \quad \left[\matrix{1 & 0 & 0 \cr 0 & 1 & 0 \cr 0 & 0 & 1 \cr}\right]$

The vectors are independent. Three independent vectors in $\real^3$ must form a basis.

(b) Find the components of relative to ${\cal B}$ .

I must find numbers a, b, and c such that

$\left[\matrix{15 \cr -1 \cr 2 \cr}\right] = a \cdot \left[\matrix{1 \cr 0 \cr 1 \cr}\right] + b\cdot \left[\matrix{2 \cr -1 \cr 1 \cr}\right] + c\cdot \left[\matrix{3 \cr 1 \cr 0 \cr}\right].$

This is equivalent to the matrix equation

$\left[\matrix{1 & 2 & 3 \cr 0 & -1 & 1 \cr 1 & 1 & 0 \cr}\right] \left[\matrix{a \cr b \cr c \cr}\right] = \left[\matrix{15 \cr -1 \cr 2 \cr}\right].$

Set up the matrix for the system and row reduce to solve:

$\left[\matrix{1 & 2 & 3 & 15 \cr 0 & -1 & 1 & -1 \cr 1 & 1 & 0 & 2 \cr}\right] \quad \to \quad \left[\matrix{1 & 0 & 0 & -2 \cr 0 & 1 & 0 & 4 \cr 0 & 0 & 1 & 3 \cr}\right]$

This says , , and . Therefore, $( 15, -1, 2) = ( -2, 4, 3)_{\cal B}$ .

I'll write $v_{\cal B}$ for v relative to ${\cal B}$ and $v_{\rm std}$ for v relative to the standard basis. The matrix equation in (b)

$\left[\matrix{1 & 2 & 3 \cr 0 & -1 & 1 \cr 1 & 1 & 0 \cr}\right] \left[\matrix{a \cr b \cr c \cr}\right] = \left[\matrix{15 \cr -1 \cr 2 \cr}\right]$

says

$\left[\matrix{1 & 2 & 3 \cr 0 & -1 & 1 \cr 1 & 1 & 0 \cr}\right] v_{\cal B} = v_{\rm std}.$

In (b), I knew $v_{\rm std}$ and I wanted $v_{\cal B}$ ; this time it's the other way around. So I simply put $( 7, -2, 2)_{\cal B}$ into the $v_{\cal B}$ spot and multiply:

$\left[\matrix{1 & 2 & 3 \cr 0 & -1 & 1 \cr 1 & 1 & 0 \cr}\right] \left[\matrix{7 \cr -2 \cr 2 \cr}\right] = \left[\matrix{9 \cr 4 \cr 5 \cr}\right].\quad\halmos$

Let me generalize the observation I made in (c).

If ${\cal B}$ is a basis for $\real^n$ --- whose elements are written in terms of the standard basis, of course --- and M is the matrix whose columns are the vectors in ${\cal B}$ , then left multiplication by M translates vectors written in terms of ${\cal B}$ to vectors written in terms of the standard basis.

$M v_{\cal B} = v_{\rm std}.$

I'll write $[{\cal B} \to {\rm std}]$ for M, and call it a translation matrix. Again, $[{\cal B} \to {\rm std}]$ translates vectors written in terms of ${\cal B}$ to vectors written in terms of the standard basis.

The inverse of a square matrix M is a matrix $M^{-1}$ such that $MM^{-1} = M^{-1}M = I$ , where I is the identity matrix. If I multiply the last equation on the left by $M^{-1}$ , I get

$M^{-1}M v_{\cal B} = M^{-1}v_{\rm std}, \quad\hbox{or}\quad v_{\cal B} = M^{-1}v_{\rm std}.$

In words, this means:

Left multiplication by $M^{-1}$ translates vectors from the standard basis to ${\cal B}$ .

This means that $M^{-1} = [{\rm std} \to {\cal B}]$ . Dispensing with M, I can say that

$[{\rm std} \to {\cal B}] = [{\cal B} \to {\rm std}]^{-1}.$

In the example above, left multiplication by the following matrix translates vectors from ${\cal B}$ to the standard basis:

$[{\cal B} \to {\rm std}] = \left[\matrix{ 1 & 2 & 3 \cr 0 & -1 & 1 \cr 1 & 1 & 0 \cr}\right].$

The inverse of is

$[{\rm std} \to {\cal B}] = [{\cal B} \to {\rm std}]^{-1} = \left[\matrix{-\dfrac{1}{4} & \dfrac{3}{4} & \dfrac{5}{4} \cr \noalign{\vskip2pt} \dfrac{1}{4} & -\dfrac{3}{4} & -\dfrac{1}{4} \cr \noalign{\vskip2pt} \dfrac{1}{4} & \dfrac{1}{4} & -\dfrac{1}{4} \cr}\right].$

Left multiplication by this matrix translates vectors from the standard basis to ${\cal B}$ .

Example. (Translating vectors from one basis to another) The translation analogy is a useful one, since it makes it easy to see how to set up arbitrary changes of basis.

For example, suppose

${\cal B}' = \left\{\left[\matrix{1 \cr -1 \cr 2 \cr}\right], \left[\matrix{2 \cr 0 \cr 1 \cr}\right], \left[\matrix{1 \cr 1 \cr 1 \cr}\right]\right\}$

is another basis for $\real^3$ .

Here's how to translate vectors from ${\cal B}'$ to ${\cal B}$ :

$[{\cal B}' \rightarrow {\cal B}] = [{\rm standard} \rightarrow {\cal B}] [{\cal B}' \rightarrow {\rm standard}].$

Remember that the product $[{\rm standard} \rightarrow {\cal B}] [{\cal B}' \rightarrow {\rm standard}]$ is read from right to left! Thus, the composite operation $[{\rm standard} \rightarrow {\cal B}] [{\cal B}' \rightarrow {\rm standard}]$ translates a ${\cal B}'$ vector to a standard vector, and then translates the resulting standard vector to a ${\cal B}$ vector. Moreover, I have matrices which perform each of the right-hand operations.

This matrix translates vectors from ${\cal B}'$ to the standard basis:

$\left[\matrix{1 & 2 & 1 \cr -1 & 0 & 1 \cr 2 & 1 & 1 \cr}\right].$

This matrix translates vectors from the standard basis to ${\cal B}$ :

Therefore, multiplication by the following matrix will translate vectors from ${\cal B}'$ to ${\cal B}$ :

$\left[\matrix{-\dfrac{1}{4} & \dfrac{3}{4} & \dfrac{5}{4} \cr \noalign{\vskip2pt} \dfrac{1}{4} & -\dfrac{3}{4} & -\dfrac{1}{4} \cr \noalign{\vskip2pt} \dfrac{1}{4} & \dfrac{1}{4} & -\dfrac{1}{4} \cr}\right] \left[\matrix{1 & 2 & 1 \cr -1 & 0 & 1 \cr 2 & 1 & 1 \cr}\right] = \left[\matrix{\dfrac{3}{2} & \dfrac{3}{4} & \dfrac{7}{4} \cr \noalign{\vskip2pt} \dfrac{1}{2} & \dfrac{1}{4} & -\dfrac{3}{4} \cr \noalign{\vskip2pt} -\dfrac{1}{2} & \dfrac{1}{4} & \dfrac{1}{4} \cr}\right]. \quad\halmos$

Contact information

Bruce Ikenaga's Home Page