The Column Space of a Matrix

Definition. Let A be an $m \times n$ matrix. The column vectors of A are the vectors in $F^n$ corresponding to the columns of A. The column space of A is the subspace of $F^n$ spanned by the column vectors of A.

For example, consider the real matrix

$$A = \left[\matrix{1 & 0 \cr 0 & 1 \cr 0 & 0 \cr}\right].$$

The column vectors are $(1, 0, 0)$ and $(0, 1, 0)$ . The column space is the subspace of $\real^3$ spanned by these vectors. Thus, the column space consists of all vectors of the form

$$a \cdot (1, 0, 0) + b \cdot (0, 1, 0) = (a, b, 0).$$

We've seen how to find a basis for the row space of a matrix. We'll now give an algorithm for finding a basis for the column space.

First, here's a reminder about matrix multiplication. If A is an $m \times n$ matrix and $v \in F^n$ , then you can think of the multiplication $A v$ as multiplying the columns of A by the components of v:

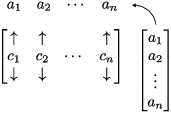
$$\hbox{\epsfysize=1in \epsffile{column-space-1.eps}}$$

This means that if $c_i$ is the i-th column of A and $v = (a_1, \ldots, a_n)$ , the product $A v$ is a linear combination of the columns of A:

$$\left[\matrix{ \uparrow & \uparrow & & \uparrow \cr c_1 & c_2 & \cdots & c_n \cr \downarrow & \downarrow & & \downarrow \cr}\right] \left[\matrix{a_1 \cr a_2 \cr \vdots \cr a_n \cr}\right] = a_1 c_1 + a_2 c_2 + \cdots + a_n c_n.$$

Proposition. Let A be a matrix, and let R be the row reduced echelon matrix which is row equivalent to A. Suppose the leading entries of R occur in columns $j_1, \ldots, j_p$ , where $j_1 < \cdots < j_p$ , and let $c_i$ denote the i-th column of A. Then $\{c_{j_1}, \ldots, c_{j_p}\}$ is independent.

Proof. Suppose that

$$a_{j_1} c_{j_1} + \cdots + a_{j_p} c_{j_p} = 0, \quad\hbox{for}\quad a_i \in F.$$

Form the vector $v = (v_i)$ , where

$$v_i = \cases{ 0 & if $i \notin \{ j_1, \ldots, j_p\}$ \cr a_i & if $i \in \{ j_1, \ldots, j_p\}$ \cr}$$

The equation above implies that $A v = 0$ .

It follows that v is in the solution space of the system $Ax = 0$ . Since $Rx = 0$ has the same solution space, $Rv = 0$ . Let $c'_i$ denote the i-th column of R. Then

$$0 = Rv = a_{j_1} c'_{j_1} + \cdots + a_{j_p} c_{j_p}.$$

However, since R is in row reduced echelon form, $c'_{j_k}$ is a vector with 1 in the k-th row and 0's elsewhere. Hence, $\{c_{j_1}, \ldots, c_{j_p}\}$ is independent, and $a_{j_1} = \cdots = a_{j_p} = 0$ .

The proof provides an algorithm for finding a basis for the column space of a matrix. Specifically, row reduce the matrix A to a row reduced echelon matrix R. If the leading entries of R occur in columns $j_1, \ldots, j_p$ , then consider the columns $c_{j_1}, \ldots, c_{j_p}$ of A. These columns form a basis for the column space of A.

Example. Find a basis for the column space of the real matrix

$$\left[\matrix{ 1 & -2 & 3 & 1 & 1 \cr 2 & 1 & 0 & 3 & 1 \cr 0 & -5 & 6 & -1 & 1 \cr 7 & 1 & 3 & 10 & 4 \cr}\right].$$

Row reduce the matrix:

$$\left[\matrix{ 1 & -2 & 3 & 1 & 1 \cr 2 & 1 & 0 & 3 & 1 \cr 0 & -5 & 6 & -1 & 1 \cr 7 & 1 & 3 & 10 & 4 \cr}\right] \quad \to \quad \left[\matrix{ 1 & 0 & 0.6 & 1.4 & 0.6 \cr 0 & 1 & -1.2 & 0.2 & -0.2 \cr 0 & 0 & 0 & 0 & 0 \cr 0 & 0 & 0 & 0 & 0 \cr}\right]$$

The leading entries occur in columns 1 and 2. Therefore, $(1, 2, 0, 7)$ and $(-2, 1, -5, 1)$ form a basis for the column space of A.

Note that if A and B are row equivalent, they don't necessarily have the same column space. For example,

$$\left[\matrix{ 1 & 2 & 1 \cr 1 & 2 & 1 \cr}\right] \matrix{\rightarrow \cr r_2 \rightarrow r_2 - r_1 \cr} \left[\matrix{ 1 & 2 & 1 \cr 0 & 0 & 0 \cr}\right].$$

However, all the elements of the column space of the second matrix have their second component equal to 0; this is obviously not true of elements of the column space of the first matrix.

Example. Find a basis for the column space of the following matrix over $\integer_3$ :

$$A = \left[\matrix{ 0 & 1 & 1 & 0 \cr 1 & 2 & 1 & 0 \cr 2 & 1 & 2 & 1 \cr}\right].$$

Row reduce the matrix:

$$\left[\matrix{ 0 & 1 & 1 & 0 \cr 1 & 2 & 1 & 0 \cr 2 & 1 & 2 & 1 \cr}\right] \matrix{\to \cr r_{1} \leftrightarrow r_{2} \cr} \left[\matrix{ 1 & 2 & 1 & 0 \cr 0 & 1 & 1 & 0 \cr 2 & 1 & 2 & 1 \cr}\right] \matrix{\to \cr r_{3} \to r_{3} + r_{1} \cr}$$

$$\left[\matrix{ 1 & 2 & 1 & 0 \cr 0 & 1 & 1 & 0 \cr 0 & 0 & 0 & 1 \cr}\right] \matrix{\to \cr r_{1} \to r_{1} + r_{2} \cr} \left[\matrix{ 1 & 0 & 2 & 0 \cr 0 & 1 & 1 & 0 \cr 0 & 0 & 0 & 1 \cr}\right]$$

The leading entries occur in columns 1, 2, and 4. Hence, columns 1, 2, and 4 of A are independent and form a basis for the column space of A:

$$\left\{\left[\matrix{0 \cr 1 \cr 2 \cr}\right], \left[\matrix{1 \cr 2 \cr 1 \cr}\right], \left[\matrix{0 \cr 0 \cr 1 \cr}\right]\right\} \quad\halmos$$

I showed earlier that you can add vectors to an independent set to get a basis. The column space basis algorithm shows how to remove vectors from a spanning set to get a basis.

$$\hbox{\epsfysize=2in \epsffile{column-space-2.eps}}$$

Example. Find a subset of the following set of vectors which forms a basis for $\real^3$ .

$$\left\{ \left[\matrix{1 \cr 2 \cr 1 \cr}\right], \left[\matrix{-1 \cr 1 \cr -1 \cr}\right], \left[\matrix{1 \cr 1 \cr 1 \cr}\right], \left[\matrix{4 \cr -1 \cr 2 \cr}\right]\right\}$$

Make a matrix with the vectors as columns and row reduce:

$$\left[\matrix{ 1 & -1 & 1 & 4 \cr 2 & 1 & 1 & -1 \cr 1 & -1 & 1 & 2 \cr}\right] \quad \to \quad \left[\matrix{ 1 & 0 & \dfrac{2}{3} & 0 \cr \noalign{\vskip2pt} 0 & 1 & -\dfrac{1}{3} & 0 \cr \noalign{\vskip2pt} 0 & 0 & 0 & 1 \cr}\right]$$

The leading entries occur in columns 1, 2, and 4. Therefore, the corresponding columns of the original matrix are independent, and form a basis for $\real^3$ :

$$\left\{ \left[\matrix{1 \cr 2 \cr 1 \cr}\right], \left[\matrix{-1 \cr 1 \cr -1 \cr}\right], \left[\matrix{4 \cr -1 \cr 2 \cr}\right]\right\}.\quad\halmos$$

Definition. Let A be a matrix. The column rank of A is the dimension of the column space of A.

This is really just a temporary definition, since we'll show that the column rank is the same as the rank we define earlier (the dimension of the row space).

Proposition. Let A be a matrix. Then

$$\hbox{rank}(A) = \hbox{column rank}(A).$$

Proof. Let R be the row reduced echelon matrix which is row equivalent to A. Suppose the leading entries of R occur in columns $j_1, \ldots, j_p$ , where $j_1 < \cdots < j_p$ , and let $c_i$ denote the i-th column of A. By the preceding lemma, $\{c_{j_1}, \ldots, c_{j_p}\}$ is independent. There is one vector in this set for each leading entry, and the number of leading entries equals the row rank. Therefore,

$$\hbox{rank}(A) \le \hbox{column rank}(A).$$

Now consider $A^T$ . This is A with the rows and columns swapped, so

$$\hbox{rank}(A^T) = \hbox{column rank}(A),$$

$$\hbox{column rank}(A^T) = \hbox{rank}(A).$$

Applying the first part of the proof to $A^T$ ,

$$\hbox{column rank}(A) = \hbox{rank}(A^T) \le \hbox{column rank}(A^T) = \hbox{rank}(A).$$

Therefore,

$$\hbox{column rank}(A) = \hbox{rank}(A).\quad\halmos$$

Proposition. Let A, B, P and Q be matrices, where P and Q are invertible. Suppose $A = P B Q$ . Then

$$\rank A = \rank B.$$

Proof. I showed earlier that $\rank M N \le \rank N$ . This was row rank; a similar proof shows that

$$\hbox{column rank}(M N) \le \hbox{column rank}(M).$$

Since row rank and column rank are the same, $\rank M N \le \rank M$ .

Now

$$\rank A = \rank P B Q \le \rank B Q = \hbox{column rank}(B Q) \le \hbox{column rank}(B) = \rank B.$$

But $B = P^{-1} A Q^{-1}$ , so repeating the computation gives $\rank B \le \rank A$ . Therefore, $\rank A = \rank B$ .

Contact information

Bruce Ikenaga's Home Page

Copyright 2023 by Bruce Ikenaga