Complex Numbers

A complex number is a number of the form , where a and b are real numbers. a is called the real part and b is called the imaginary part; the notation is

$\re (a + bi) = a, \quad \im (a + bi) = b.$

You add, subtract, and multiply complex numbers in the obvious ways:

The conjugate of complex number is obtained by flipping the sign of the imaginary part. The conjugate of is denoted $\overline{a + bi}$ or sometimes . Thus,

$\overline{a + bi} = a - bi.$

You can divide by (nonzero) complex numbers by "multiplying the top and bottom by the conjugate":

$\dfrac{a + bi}{c + di} = \dfrac{a + bi}{c + di}\cdot \dfrac{c - di}{c - di} = \dfrac{(ac + bd) + (-ad + bc)i}{c^2 + d^2}.$

With these operations, the set of complex numbers forms a field.

Example.

$\dfrac{5 - 2i}{3 + 4i} = \dfrac{5 - 2i}{3 + 4i}\cdot \dfrac{3 - 4i}{3 - 4i} = \dfrac{15 - 6i - 20i + 8i^2}{9 - 16i^2} = \dfrac{15 - 26i + 8(-1)}{9 - 16(-1)} = \dfrac{7 - 26i}{25}.$

$i^{517} = i^{516}\cdot i = (i^2)^{258}\cdot i = (-1)^{258}\cdot i = 1\cdot i = i.\quad\halmos$

The norm of a complex number is

$|a + bi| = \sqrt{a^2 + b^2}.$

Note that

$(a + bi)(\overline{a + bi}) = (a + bi)(a - bi) = a^2 + b^2 = |a + bi|^2.$

When a complex number is written in the form , it's said to be in rectangular form. There is another form for complex numbers that is useful: The polar form $re^{i\theta}$ . In this form, r and $\theta$ have the same meanings that they do in polar coordinates.

DeMoivre's formula relates the polar and rectangular forms:

$e^{i\theta} = \cos \theta + i \sin \theta.$

This key result can be proven, for example, by expanding both sides in power series. It's really useful, as you'll see in the examples below.

Observe that

$|e^{i\theta}| = |\cos \theta + i \sin \theta| = \sqrt{(\cos \theta)^2 + (\sin \theta)^2} = 1.$

Thus, $e^{i\theta}$ is a complex number of norm 1.

Example. Convert to polar form.

$3 + 4i = |3 + 4i|\cdot \dfrac{3 + 4i}{|3 + 4i|} = 5\left(\dfrac{3}{5} + \dfrac{4}{5}i\right).$

Let $\theta = \sin^{-1} \dfrac{4}{5}$ (or $\cos^{-1} \dfrac{3}{5}$ ). Then

$3 + 4i = 5(\cos \theta + i\sin \theta).\quad\halmos$

Example. ( A trick with Demoivre's formula) Find $(1 + i\sqrt{3})^8$ .

It would be tedious to try to multiply this out. Instead, I'll try to write the expression in terms of $\cos \theta + i \sin \theta$ for a good choice of $\theta$ .

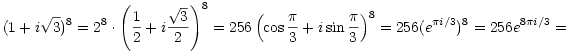
$(1 + i\sqrt{3})^8 = 2^8\cdot \left(\dfrac{1}{2} + i\dfrac{\sqrt{3}}{2}\right)^8 = 256\left(\cos \dfrac{\pi}{3} + i\sin \dfrac{\pi}{3}\right)^8 = 256(e^{\pi i/3})^8 = 256e^{8\pi i/3} =$

$256\left(\cos \dfrac{8\pi}{3} + i\sin \dfrac{8\pi}{3}\right) = 256\left(\cos \dfrac{2\pi}{3} + i\sin \dfrac{2\pi}{3}\right) = 256\left(-\dfrac{1}{2} + i\dfrac{\sqrt{3}}{2}\right) = -128 + 128i\sqrt{3}.\quad\halmos$

Example. ( Proving trig identities) Prove the angle addition formulas:

$\cos (a + b) = \cos a \cos b - \sin a \sin b.$

$\sin (a + b) = \sin a \cos b + \sin b \cos a.$

I have

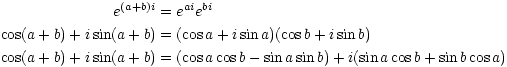
$\eqalign{e^{(a+b)i} &= e^{ai}e^{bi} \cr \cos (a + b) + i \sin (a + b) &= (\cos a + i \sin a)(\cos b + i \sin b) \cr \cos (a + b) + i \sin (a + b) &= (\cos a\cos b - \sin a \sin b) + i(\sin a \cos b + \sin b \cos a) \cr}$

Equating real and imaginary parts on the left and right sides, I get

$\cos (a + b) = \cos a \cos b - \sin a \sin b \quad\hbox{(real parts)}.$

$\sin (a + b) = \sin a \cos b + \sin b \cos a \quad\hbox{(imaginary parts)}.\quad\halmos$

Example. ( Computing integrals) Compute $\displaystyle \int e^{2x}\cos 3x\,dx$ .

Note that $\cos 3x = \re (e^{3xi})$ . Thus,

$\int e^{2x}\cos 3x\,dx = \int e^{2x} \re (e^{3xi})\,dx = \re \int e^{2x}e^{3xi}\,dx = \re \int e^{(2+3i)x}\,dx = \re \dfrac{1}{2 + 3i}e^{(2+3i)x} + c =$

$\re \dfrac{2 - 3i}{13}e^{2x}(\cos 3x + i \sin 3x) + c = \dfrac{1}{13}e^{2x} \re (2 - 3i)(\cos 3x + i\sin 3x) + c =$

$\dfrac{1}{13}e^{2x} \re \left((2\cos 3x + 3\sin 3x) + i(2\sin 3x - 3\cos 3x)\right) + c = \dfrac{1}{13}e^{2x}(2\cos 3x + 3\sin 3x) + c.\quad\halmos$

Contact information

Bruce Ikenaga's Home Page