Determinants - Uniqueness

In this section, I'll derive another formula for determinants. Using this formula, we'll be able to show that there is only one function on $n \times n$ matrices which satisfies the axioms for a determinant.

The main theorem says that a function on $n \times n$ matrices which satisfies the first two axioms for a determinant function --- linearity on the rows, and alternating (0 on matrices with two equal rows) --- is a sum of products of entries of the matrix, "scaled" by the value of the function on the identity matrix ( ). Each product of entries is formed by choosing n entries, one from each row and each column, in all possible ways; the products get a plus or minus sign according to the sign of the permutation that the chosen entries "represent".

Theorem. Let R be a commutative ring with identity. If $D: M(n, r) \rightarrow R$ is linear in each row and is 0 on matrices with equal rows, then

$D(A) = \sum_{\sigma \in S_n} \sgn(\sigma) A_{1 \sigma(1)} \cdots A_{n \sigma(n)} D(I).$

Proof. This proof is a little complicated; if you wish to skip it for now, at least try to understand the statement of the theorem (and see the discussion that follows).

Write the matrix in terms of its rows:

$A = \left[\matrix{ \leftarrow & r_1 & \rightarrow \cr \leftarrow & r_2 & \rightarrow \cr & \vdots & \cr \leftarrow & r_n & \rightarrow \cr}\right].$

Notice that the first row of A can be written this way:

$r_1 = \left[\matrix{A_{1 1} & A_{1 2} & \cdots & A_{1 n} \cr}\right] = A_{1 1} \cdot \left[\matrix{1 & 0 & \cdots & 0 \cr}\right] + A_{1 2} \cdot \left[\matrix{0 & 1 & \cdots & 0 \cr}\right] + \cdots + A_{1 n} \cdot \left[\matrix{0 & 0 & \cdots & 1 \cr}\right] =$

$A_{1 1} e_1 + A_{1 2} e_2 + \cdots A_{1 n} e_n$

Here is the j-th standard basis vector (equivalently, the j-th row of the identity matrix). So in summation notation,

$r_1 = \sum_j A_{1 j} e_j.$

I can use linearity applied to row 1 to expand the determinant of A into a sum of determinants:

$D(A) = D \left[\matrix{ \leftarrow & \sum_j A_{1 j} e_j & \rightarrow \cr \leftarrow & r_2 & \rightarrow \cr & \vdots & \cr \leftarrow & r_n & \rightarrow \cr}\right] = \sum_j A_{1 j} D\left[ \matrix{\leftarrow & e_j & \rightarrow \cr \leftarrow & r_2 & \rightarrow \cr & \vdots & \cr \leftarrow & r_n & \rightarrow \cr}\right].$

In the same way,

$r_2 = \sum_j A_{2 j} e_j.$

Use linearity applied to row 2 to expand the determinant terms in the last D-sum:

$D(A) = \sum_j \sum_k A_{1 j} A_{2 k} D \left[\matrix{\leftarrow & e_j & \rightarrow \cr \leftarrow & e_k & \rightarrow \cr & \vdots & \cr \leftarrow & r_n & \rightarrow \cr}\right].$

Continue in this way for all n rows. I'll switch notation and use $j_1, j_2, \ldots, j_n$ as the summation indices:

$D(A) = \sum_{j_1} \sum_{j_2} \ldots \sum_{j_n} A_{1 j_1} A_{2 j_2} \cdots A_{n j_n} D \left[\matrix{ \leftarrow & e_{j_1} & \rightarrow \cr \leftarrow & e_{j_2} & \rightarrow \cr & \vdots & \cr \leftarrow & e_{j_n} & \rightarrow \cr}\right].$

If two of the j's are equal, then the e's are equal --- e.g. if , then $e_{j_3} = e_{j_7}$ . But D is 0 on matrices with equal rows. So terms with two of the j's equal are 0. Hence, I only need to consider terms where all the j's are distinct numbers in the set $\{1, 2, \ldots n\}$ . This means that $\{j_1, j_2, \ldots, j_n\}$ is a permutation of $\{1, 2, \ldots, n\}$ . So I can just sum over all permutations in $\sigma \in S_n$ :

$D(A) = \sum_{\sigma \in S_n} A_{1 \sigma(1)} A_{2 \sigma(2)} \cdots A_{n \sigma(n)} D \left[\matrix{\leftarrow & e_{\sigma(1)} & \rightarrow \cr \leftarrow & e_{\sigma(2)} & \rightarrow \cr & \vdots & \cr \leftarrow & e_{\sigma(n)} & \rightarrow \cr}\right].$

Consider the last matrix:

$\left[\matrix{ \leftarrow & e_{\sigma(1)} & \rightarrow \cr \leftarrow & e_{\sigma(2)} & \rightarrow \cr & \vdots & \cr \leftarrow & e_{\sigma(n)} & \rightarrow \cr}\right].$

Each of the e's is a standard basis vector. But the standard basis vectors are the rows of the $n \times n$ identity matrix. Thus, this matrix is just the identity matrix with its rows permuted by $\sigma$ . Every permutation is a product of transpositions. By an earlier lemma, since D is linear on the rows and is 0 for matrices with equal rows, a transposition (i.e. a row swap) multiplies the value of D by -1. Hence,

$D \left[\matrix{ \leftarrow & e_{\sigma(1)} & \rightarrow \cr \leftarrow & e_{\sigma(2)} & \rightarrow \cr & \vdots & \cr \leftarrow & e_{\sigma(n)} & \rightarrow \cr}\right] = \sgn(\sigma) D(I).$

Therefore,

$D(A) = \sum_{\sigma \in S_n} A_{1 \sigma(1)} A_{2 \sigma(2)} \cdots A_{n \sigma(n)} \sgn(\sigma) D(I).\quad\halmos$

Corollary. Let R be a commutative ring with identity, and let $A \in M(n, R)$ .

$\det A = \sum_{\sigma \in S_n} \sgn(\sigma) A_{1 \sigma(1)} \cdots A_{n \sigma(n)}.$

Proof. Since the determinant function $\det$ defined by expansion by cofactors is alternating and linear in each row, it satisfies the conditions of the theorem. Since $\det I = 1$ , the formula in the theorem becomes

$\det A = \sum_{\sigma \in S_n} \sgn(\sigma) A_{1 \sigma(1)} \cdots A_{n \sigma(n)}.\quad\halmos$

I'll call this the permutation formula for the determinant.

Let's try to understand a typical product in the sum: $A_{1 \sigma(1)} A_{2 \sigma(2)} \cdots A_{n \sigma(n)}$ . You can see that the row indices go from 1 to n, so we're choosing one entry of the matrix from each row. The column indices are $\sigma(1)$ , $\sigma(2)$ , ... $\sigma(n)$ . This is a permutation of $\{1, 2, \ldots n\}$ , which means each of the numbers from 1 to n is chosen exactly once. This means that we're also choosing the entries so that one comes from each column. We're summing over all permutations of $\{1, 2, \ldots n\}$ , so we're choosing entries for our products in all such ways. Let's see how this looks for small matrices.

Consider a $2 \times 2$ matrix:

$\left[\matrix{a & b \cr c & d \cr}\right]$

I have to choose 2 entries at a time, so the 2 entries come from different rows and columns. I multiply the 2 chosen entries to get one of the product terms. There are ways to do this; they are

$a\ d, \quad b\ c$

Next, consider a $3 \times 3$ matrix:

$\left[\matrix{ a & b & c \cr d & e & f \cr g & h & i \cr}\right]$

I have to choose 3 entries at a time, so the 3 entries come from different rows and columns. I multiply the 3 entries to get one of the product terms, and I do this in all possible ways. There are ways to do this; they are

$a\ e\ i, \quad a\ f\ h, \quad b\ d\ i, \quad b\ f\ g, \quad c\ d\ h, \quad c\ e\ g$

For a $4 \times 4$ matrix, there will be products!

The products we're getting will each get a plus or minus sign, depending on the permutation the product represents. We'll see how to determine the signs in the example below. Finally, all the signed products are added up to get the determinant.

Example. Use the permutation formula to compute the following real determinant:

$\det \left[\matrix{ 2 & 1 & 4 \cr 1 & -1 & 2 \cr 5 & 3 & 1 \cr}\right]$

I have to choose 3 entries from the matrix at a time, in such a way that there is one entry from each row and each column. For each such choice, I take the product of the three elements and multiply by the sign of the permutation of the elements, which I'll describe below. Finally, I add up the results.

In order to do this systematically, focus on the first column. I can choose 2, 1, or 5 from column 1.

If I choose 2 from column 1, I can either choose -1 from column 2 and 1 from column 3, or 3 from column 2 and 2 from column 3. (Remember that I can't have two elements from the same row or column.)

$\left[\matrix{ 2 & \ast & \ast \cr \ast & -1 & \ast \cr \ast & \ast & 1 \cr}\right] \quad \left[\matrix{ 2 & \ast & \ast \cr \ast & \ast & 2 \cr \ast & 3 & \ast \cr}\right]$

If I choose 1 from column 1, I can either choose 1 from column 2 and 1 from column 3, or 3 from column 2 and 4 from column 3.

$\left[\matrix{ \ast & 1 & \ast \cr 1 & \ast & \ast \cr \ast & \ast & 1 \cr}\right] \quad \left[\matrix{ \ast & \ast & 4 \cr 1 & \ast & \ast \cr \ast & 3 & \ast \cr}\right]$

Finally, if I choose 5 from column 1, I can either choose 1 from column 2 and 2 from column 3, or -1 from column 2 and 4 from column 3.

$\left[\matrix{ \ast & 1 & \ast \cr \ast & \ast & 2 \cr 5 & \ast & \ast \cr}\right] \quad \left[\matrix{ \ast & \ast & 4 \cr \ast & -1 & \ast \cr 5 & \ast & \ast \cr}\right]$

This gives me 6 products:

$(2)(-1)(1) \quad (2)(3)(2) \quad (1)(1)(1) \quad (1)(3)(4) \quad (5)(1)(2) \quad (5)(-1)(4)$

Next, I have to attach a sign to each product. To do this, I count the number of row swaps I need to move the 1's in the identity matrix into the same positions as the numbers in the product. I'll illustrate with two examples.

$\left[\matrix{ \ast & \ast & 4 \cr 1 & \ast & \ast \cr \ast & 3 & \ast \cr}\right]: \qquad \left[\matrix{ 1 & 0 & 0 \cr 0 & 1 & 0 \cr 0 & 0 & 1 \cr}\right] \matrix{\to \cr r_1 \leftrightarrow r_2 \cr} \left[\matrix{ 0 & 1 & 0 \cr 1 & 0 & 0 \cr 0 & 0 & 1 \cr}\right] \matrix{\to \cr r_1 \leftrightarrow r_3 \cr} \left[\matrix{ 0 & 0 & 1 \cr 1 & 0 & 0 \cr 0 & 1 & 0 \cr}\right]$

It took 2 row swaps to move the 1's into the same positions as 1, 3, and 4. Since 2 is even, the sign of is .

$\left[\matrix{ \ast & \ast & 4 \cr \ast & -1 & \ast \cr 5 & \ast & \ast \cr}\right]: \qquad \left[\matrix{ 1 & 0 & 0 \cr 0 & 1 & 0 \cr 0 & 0 & 1 \cr}\right] \matrix{\to \cr r_1 \leftrightarrow r_3 \cr} \left[\matrix{ 0 & 0 & 1 \cr 0 & 1 & 0 \cr 1 & 0 & 0 \cr}\right]$

It took 1 row swap to move the 1's into the same positions as 7, 5, and 3. Since 1 is odd, the sign of is -1.

Continuing in this fashion, I get

$\det \left[\matrix{ 2 & 1 & 4 \cr 1 & -1 & 2 \cr 5 & 3 & 1 \cr}\right] = (2)(-1)(1) - (2)(3)(2) - (1)(1)(1) + (1)(3)(4) + (5)(1)(2) - (5)(-1)(4) = 27.\quad\halmos$

Notice how ugly the computation was! While the permutation formula can be used for computations, it's easier to use row or column operations or expansion by cofactors. The main point of the permutation formula lies in the following Corollary. It says there is only one function on $n \times n$ matrices which satisfies the three axioms for a determinant --- the determinant function is unique. Row reduction, expansion by cofactors, and the permutation formula give different ways of computing the same thing.

The permutation formula is connected to a trick for computing determinants of $3 \times 3$ matrices. You may have seen this trick in other math courses, or in physics courses. I'll illustrate with the matrix in the last example.

Warning: This only works on determinants which are $3 \times 3$ !

Begin by making copies of the first two columns of the matrix. Put the copies to the right of the original matrix:

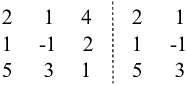
$\hbox{\epsfysize=0.75in \epsffile{determinants-uniqueness-1.eps}}$

Next, draw diagonal lines through the elements as shown below. Three lines down and to the right, three lines up and to the right:

$\hbox{\epsfysize=0.75in \epsffile{determinants-uniqueness-2.eps}}$

Form products by multiplying the elements along each line. The products of the "down and right" lines get plus signs, and the products of the "down and left" lines get minus signs:

You can see that we got the same terms as we got with the permutation formula, with the factors and the terms in a different order.

Again, I emphasize that this trick only works on matrices which are $3 \times 3$ ! You can't use it on matrices of any other size. It's not bad for $3 \times 3$ determinants you're computing by hand, so feel free to use it if you wish. Don't try to use it on determinants which are $2 \times 2$ , $4 \times 4$ , and so on.

Corollary. Let R be a commutative ring with identity. There is a unique determinant function $|\cdot|: M(n, R) \rightarrow R$ .

Proof. The permutation formula says

$\det A = \sum_{\sigma \in S_n} \sgn(\sigma) A_{1 \sigma(1)} \cdots A_{n \sigma(n)}.$

But the right side only depends on the entries of the matrix A. So is completely determined by A, and there can be only one determinant function on $n \times n$ matrices.

We know that the determinant function defined by cofactor expansion satisfies the axioms for a determinant function. Therefore, it is the only determinant function on $n \times n$ matrices.

This doesn't mean that you can't compute the determinant in different ways; in fact, the permutation formula gives a different way of computing determinants than cofactor expansion. To say that there's only one determinant function means that any function satisfying the determinant axioms will give the same answer as any other function satisfying the determinant axioms, for a given matrix.

Remark. Here's another way to express the theorem. Suppose $\det$ denotes the determinant function on . If $D: M(n, r) \rightarrow R$ is alternating and linear in each row, then

$D(A) = (\det A) D(I).$

In other words, a function which satisfies the first two axioms for a determinant function is a multiple of the "real" determinant function, the multiple being the value the function takes on the identity matrix. In the case of the "real" determinant function, the third axiom says $\det I = 1$ , so the multiple is 1 and D is the "real" determinant function.

Contact information

Bruce Ikenaga's Home Page