Expansion by Cofactors

I gave the axioms for determinant functions, and it seems from our examples that we could compute determinants using only the axioms, or using row operations. But this doesn't prove that there actually are any functions which satisfy the axioms; maybe our computations were just luck.

We can settle this question by actually constructing a function which satisfies the axioms for a determinant. I'll do this using expansion by cofactors, which also gives us another way of computing determinants. The construction is inductive: We'll get started by giving formulas for the determinants of $1 \times 1$ and $2 \times 2$ matrices. Note that it's not enough to give a formula; we also have to check that the formula gives a function which satisfies the determinant axioms.

Next, the cofactor construction will allow us to go from a determinant function on $(n - 1) \times (n - 1)$ matrices to a determinant function on $n \times n$ matrices (matrices "one size bigger"). By induction, this will give a determinant function on $n \times n$ matrices for all $n \ge 1$ .

Let's get started with the easy cases.

For a $1 \times 1$ matrix, the determinant is just the single entry:

$$D \left[\matrix{a \cr}\right] = a.$$

The axioms are easy to check. If $a, x, y \in R$ , then

$$D \left[\matrix{a x + y \cr}\right] = a x + y = a \cdot D \left[\matrix{x \cr}\right] + D \left[\matrix{y \cr}\right].$$

Thus, the linearity axiom holds.

Since the matrix only has one row, it can't have two equal rows, and the second axiom holds vacuously. Finally, the $1 \times 1$ identity matrix has determinant 1.

I could start the induction at this point, but it's useful to give an explicit formula for the determinant of a $2 \times 2$ matrix. You may have seen this in (say) a multivariable calculus course.

Proposition. Define $D: M(2, R) \rightarrow R$ by

$$D \left[\matrix{ a & b \cr c & d \cr}\right] = a d - b c.$$

Then D is a determinant function on $M(2, R)$ .

Proof. I will check that the function is linear in each row.

$$D \left[\matrix{ k a + a' & k b + b' \cr c & d \cr}\right] = k a d + a' d - k b c - b' c = k (a d - b c) + (a' d - b' c) = k D \left[\matrix{ a & b \cr c & d \cr}\right] + D \left[\matrix{ a' & b' \cr c & d \cr}\right].$$

$$D \left[\matrix{ a & b \cr k c + c' & k d + d' \cr}\right] = a (k d + d') - b (k c + c') = k (a d - b c) + (a d' - b c') = k D \left[\matrix{ a & b \cr c & d \cr}\right] + D \left[\matrix{ a & b \cr c' & d' \cr}\right].$$ This proves linearity.

Suppose the two rows are equal. Then

$$D \left[\matrix{ a & b \cr a & b \cr}\right] = a b - a b = 0.$$

Therefore, Axiom 2 holds.

Finally,

$$D \left[\matrix{1 & 0 \cr 0 & 1 \cr}\right] = 1.$$

All three axioms have been verified, so D is a determinant function.

To save writing, we often write

$$\left|\matrix{1 & 2 \cr 3 & 4 \cr}\right| \quad\hbox{for}\quad D \left[\matrix{1 & 2 \cr 3 & 4 \cr}\right].$$

This is okay, since we'll eventually find out that there is only one determinant function on $n \times n$ matrices. You can also write "det" for the determinant function.

For example, on $M(2, \real)$ ,

$$\left|\matrix{ 1 & 2 \cr 3 & 4 \cr}\right| = 4 - 6 = -2.$$

Let's move on to the inductive step for the main result. Earlier I discussed the connection between "swapping two rows multiplies the determinant by -1" and "when two rows are equal the determinant is 0". The next lemma is another piece of this picture. It says for a function which is linear in the rows, if "when two adjacent rows are equal the determinant is 0", then "swapping two rows multiplies the determinant by -1". (Axiom 2 does not require that the two equal rows be adjacent.) It's a technical result which is used in the proof of the main theorem and nowhere else, and the proof is rather technical as well. You could skip it and refer to the result when it's needed in the main theorem proof.

Lemma. Let $f: M(n, r) \rightarrow R$ be a function which is linear in each row and satisfies $f(A) = 0$ whenever two adjacent rows are equal. Then swapping any two rows multiplies the value of f by -1.

Proof. First, I'll show that swapping two adjacent rows multiplies the value of f by -1. I'll show the required manipulations in schematic form. The adjacent rows are those with the x's and y's; as usual, the vertical dots represent the other rows, which are the same in all of the matrices.

$$f\left[\matrix{& \vdots & \cr \leftarrow & x & \rightarrow \cr \leftarrow & y & \rightarrow \cr & \vdots & \cr}\right] = f\left[\matrix{& \vdots & \cr \leftarrow & y + (x - y) & \rightarrow \cr \leftarrow & y & \rightarrow \cr & \vdots & \cr}\right] = f\left[\matrix{& \vdots & \cr \leftarrow & y & \rightarrow \cr \leftarrow & y & \rightarrow \cr & \vdots & \cr}\right] + f\left[\matrix{& \vdots & \cr \leftarrow & x - y & \rightarrow \cr \leftarrow & y & \rightarrow \cr & \vdots & \cr}\right] =$$

$$f\left[\matrix{& \vdots & \cr \leftarrow & x - y & \rightarrow \cr \leftarrow & y & \rightarrow \cr & \vdots & \cr}\right] = f\left[\matrix{& \vdots & \cr \leftarrow & x - y & \rightarrow \cr \leftarrow & x + (y - x) & \rightarrow \cr & \vdots & \cr}\right] = f\left[\matrix{& \vdots & \cr \leftarrow & x - y & \rightarrow \cr \leftarrow & x & \rightarrow \cr & \vdots & \cr}\right] + f\left[\matrix{& \vdots & \cr \leftarrow & x - y & \rightarrow \cr \leftarrow & y - x & \rightarrow \cr & \vdots & \cr}\right] =$$

$$f\left[\matrix{& \vdots & \cr \leftarrow & x & \rightarrow \cr \leftarrow & x & \rightarrow \cr & \vdots & \cr}\right] - f\left[\matrix{& \vdots & \cr \leftarrow & y & \rightarrow \cr \leftarrow & x & \rightarrow \cr & \vdots & \cr}\right] - f\left[\matrix{& \vdots & \cr \leftarrow & x - y & \rightarrow \cr \leftarrow & x - y & \rightarrow \cr & \vdots & \cr}\right] = -f\left[\matrix{& \vdots & \cr \leftarrow & y & \rightarrow \cr \leftarrow & x & \rightarrow \cr & \vdots & \cr}\right].$$

Next, I'll show that you can swap any two rows by swapping adjacent rows and odd number of times. Then since each swap multiplies f by -1, and since $(-1)^{(\hbox{odd number})} = -1$ , it follows that swapping two non-adjacent rows multiplies the value of f by -1.

To illustrate the idea, suppose the rows to be swapped are rows 1 and n. I'll indicate how to do the swaps by just displaying the row numbers. First, I swap row 1 with the adjacent row below it $n - 1$ times to move it from the top of the matrix to the n-th (bottom) position:

$$\left[\matrix{ \longleftarrow r_1 \longrightarrow \cr \longleftarrow r_2 \longrightarrow \cr \longleftarrow r_3 \longrightarrow \cr \vdots \longleftarrow r_{n - 2} \longrightarrow \cr \longleftarrow r_{n - 1} \longrightarrow \cr \longleftarrow r_n \longrightarrow \cr}\right] \to \left[\matrix{ \longleftarrow r_2 \longrightarrow \cr \longleftarrow r_1 \longrightarrow \cr \longleftarrow r_3 \longrightarrow \cr \vdots \longleftarrow r_{n - 2} \longrightarrow \cr \longleftarrow r_{n - 1} \longrightarrow \cr \longleftarrow r_n \longrightarrow \cr}\right] \to \left[\matrix{ \longleftarrow r_2 \longrightarrow \cr \longleftarrow r_3 \longrightarrow \cr \longleftarrow r_1 \longrightarrow \cr \vdots \longleftarrow r_{n - 2} \longrightarrow \cr \longleftarrow r_{n - 1} \longrightarrow \cr \longleftarrow r_n \longrightarrow \cr}\right] \to \cdots \to$$

$$\left[\matrix{ \longleftarrow r_2 \longrightarrow \cr \longleftarrow r_3 \longrightarrow \cr \longleftarrow r_4 \longrightarrow \cr \vdots \longleftarrow r_1 \longrightarrow \cr \longleftarrow r_{n - 1} \longrightarrow \cr \longleftarrow r_n \longrightarrow \cr}\right] \to \left[\matrix{ \longleftarrow r_2 \longrightarrow \cr \longleftarrow r_3 \longrightarrow \cr \longleftarrow r_4 \longrightarrow \cr \vdots \longleftarrow r_{n - 1} \longrightarrow \cr \longleftarrow r_1 \longrightarrow \cr \longleftarrow r_n \longrightarrow \cr}\right] \to \left[\matrix{ \longleftarrow r_2 \longrightarrow \cr \longleftarrow r_3 \longrightarrow \cr \longleftarrow r_4 \longrightarrow \cr \vdots \longleftarrow r_{n - 1} \longrightarrow \cr \longleftarrow r_n \longrightarrow \cr \longleftarrow r_1 \longrightarrow \cr}\right]$$

Next, I swap (the old) row n with the adjacent row above it $n - 2$ times to move it to the top of the matrix:

$$\left[\matrix{ \longleftarrow r_2 \longrightarrow \cr \longleftarrow r_3 \longrightarrow \cr \longleftarrow r_4 \longrightarrow \cr \vdots \longleftarrow r_{n - 1} \longrightarrow \cr \longleftarrow r_n \longrightarrow \cr \longleftarrow r_1 \longrightarrow \cr}\right] \to \left[\matrix{ \longleftarrow r_2 \longrightarrow \cr \longleftarrow r_3 \longrightarrow \cr \longleftarrow r_4 \longrightarrow \cr \vdots \longleftarrow r_n \longrightarrow \cr \longleftarrow r_{n - 1} \longrightarrow \cr \longleftarrow r_1 \longrightarrow \cr}\right] \to \left[\matrix{ \longleftarrow r_2 \longrightarrow \cr \longleftarrow r_3 \longrightarrow \cr \longleftarrow r_4 \longrightarrow \cr \vdots \longleftarrow r_{n - 2} \longrightarrow \cr \longleftarrow r_{n - 1} \longrightarrow \cr \longleftarrow r_1 \longrightarrow \cr}\right] \to \cdots \to$$

$$\left[\matrix{ \longleftarrow r_2 \longrightarrow \cr \longleftarrow r_3 \longrightarrow \cr \longleftarrow r_n \longrightarrow \cr \vdots \longleftarrow r_{n - 2} \longrightarrow \cr \longleftarrow r_{n - 1} \longrightarrow \cr \longleftarrow r_1 \longrightarrow \cr}\right] \to \left[\matrix{ \longleftarrow r_2 \longrightarrow \cr \longleftarrow r_n \longrightarrow \cr \longleftarrow r_3 \longrightarrow \cr \vdots \longleftarrow r_{n - 2} \longrightarrow \cr \longleftarrow r_{n - 1} \longrightarrow \cr \longleftarrow r_1 \longrightarrow \cr}\right] \to \left[\matrix{ \longleftarrow r_n \longrightarrow \cr \longleftarrow r_2 \longrightarrow \cr \longleftarrow r_3 \longrightarrow \cr \vdots \longleftarrow r_{n - 2} \longrightarrow \cr \longleftarrow r_{n - 1} \longrightarrow \cr \longleftarrow r_1 \longrightarrow \cr}\right]$$

The original rows 1 and n have swapped places, and I needed $(n - 1) + (n - 2) = 2 n - 3$ swaps of adjacent rows to do this. Now $2 n - 3$ is an odd number, and $(-1)^{2 n - 3} = -1$ .

In general, if you want to swap row i and row j, where $i < j$ , following the procedure above will require that you swap $2 j - 2 i - 1$ adjacent rows, an odd number. Once again, $(-1)^{2 j - 2 i - 1} = -1$ .

Thus, swapping two non-adjacent rows multiplies the value of f by -1.

Definition. Let $A \in M(n, r)$ . Let $A(i \mid j)$ be the $(n - 1) \times (n - 1)$ matrix obtained by deleting the i-th row and j-th column of A. If D is a determinant function, then $D[A(i \mid j)]$ is called the $(i, j)^{\rm th}$ minor of A.

In the picture below, the i-th row and j-th column are shown in gray; they will be deleted, and the remaining $(n - 1) \times (n - 1)$ matrix is $A(i \mid j)$ . Its determinant is the $(i, j)^{\rm th}$ minor.

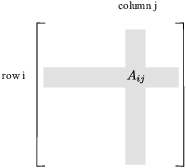
$$\hbox{\epsfysize=1.5in \epsffile{expansion-by-cofactors-1.eps}}$$

The $(i, j)^{\rm th}$ cofactor of A is $(-1)^{i + j}$ times the $(i, j)^{\rm th}$ minor, i.e. $(-1)^{i + j}\cdot D[A(i \mid j)]$ .

Example. Consider the real matrix

$$A = \left[\matrix{1 & 2 & 3 \cr 4 & 5 & 6 \cr 7 & 8 & 9 \cr}\right].$$

Find the $(2, 3)^{\rm th}$ minor and the $(2, 3)^{\rm th}$ cofactor.

To find the $(2, 3)^{\rm th}$ minor, remove the $2^{\rm nd}$ row and the $3^{\rm rd}$ column (i.e. the row and column containing the $(2, 3)^{\rm th}$ element):

$$\left[\matrix{1 & 2 & * \cr * & * & * \cr 7 & 8 & * \cr}\right].$$

The $(2, 3)^{\rm th}$ minor is the determinant of what's left:

$$\left|\matrix{1 & 2 \cr 7 & 8 \cr}\right| = 8 - 14 = -6.$$

To get the $(2, 3)^{\rm th}$ cofactor, multiply this by $(-1)^{2 + 3} = (-1)^5 = -1$ . The $(2, 3)^{\rm th}$ cofactor is $(-1)\cdot (-6) = 6$ .

Note: The easy way to remember whether to multiply by $+1$ or -1 is to make a checkboard pattern of +'s and -'s:

$$\left[\matrix{+ & - & + \cr - & + & - \cr + & - & + \cr}\right].$$

Use the sign in the $(i, j)^{\rm th}$ position. For example, there's a minus sign in the $(2, 3)^{\rm th}$ position, which agrees with the sign I computed using $(-1)^{i + j}$ .

The main result says that we may use cofactors to extend a determinant function on $(n - 1) \times (n - 1)$ matrices to a determinant function on $n \times n$ matrices.

Theorem. ( Expansion by cofactors) Let R be commutative ring with identity, and let C be a determinant function on $M(n - 1, R)$ . Let $A \in M(n, R)$ . For any $j \in \{1, \ldots, n\}$ , define

$$D(A) = \sum_{i = 1}^n (-1)^{i + j} A_{i j} C\left(A(i \mid j)\right).$$

Then D is a determinant function on $M(n, R)$ .

Notice that the summation is on i, which is the row index. The index j is fixed, and it indexes columns. This means you're moving down the $j^{\rm th}$ column as you sum. Consequently, this is a cofactor expansion by columns.

Proof. C is the "known" determinant function on $(n - 1) \times (n - 1)$ matrices ($M(n - 1, R)$ ), whereas D is the determinant function on $n \times n$ matrices ($M(n, R)$ ) that we're trying to construct. We're using C to build D, and the problem here is to verify that D satisfies the determinant axioms. Thus, I need to show that D is linear in each row, D is alternating, and $D(I) = 1$ .

This proof is moderately difficult; I've tried to write out the details and illustrate with pictures, but don't get discouraged if you find it challenging to follow.

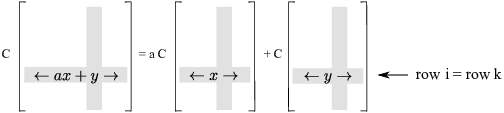
Linearity: I'll prove linearity in row k. Let $a \in R$ , $x, y \in R^n$ . I want to prove that

$$D \left[\matrix{ \leftarrow & r_1 & \rightarrow \cr & \vdots & \cr \leftarrow & a x + y & \rightarrow \cr & \vdots & \cr \leftarrow & r_n & \rightarrow \cr}\right] = a \cdot D \left[\matrix{ \leftarrow & r_1 & \rightarrow \cr & \vdots & \cr \leftarrow & x & \rightarrow \cr & \vdots & \cr \leftarrow & r_n & \rightarrow \cr}\right] + D \left[\matrix{ \leftarrow & r_1 & \rightarrow \cr & \vdots & \cr \leftarrow & y & \rightarrow \cr & \vdots & \cr \leftarrow & r_n & \rightarrow \cr}\right].$$

All the action is taking place in the k-th row --- the one with the x's and y's --- and the other rows are the same in the three matrices.

Label the three matrices above:

$$P = \left[\matrix{ \leftarrow & r_1 & \rightarrow \cr & \vdots & \cr \leftarrow & a x + y & \rightarrow \cr & \vdots & \cr \leftarrow & r_n & \rightarrow \cr}\right], \quad Q = \left[\matrix{ \leftarrow & r_1 & \rightarrow \cr & \vdots & \cr \leftarrow & x & \rightarrow \cr & \vdots & \cr \leftarrow & r_n & \rightarrow \cr}\right], \quad R = \left[\matrix{ \leftarrow & r_1 & \rightarrow \cr & \vdots & \cr \leftarrow & y & \rightarrow \cr & \vdots & \cr \leftarrow & r_n & \rightarrow \cr}\right].$$

The equation to be proved is

$$D(P) = a D(Q) + D(R).$$

If I expand the $D(\cdot)$ terms by cofactors in this equation, I get

$$\sum_{i = 1}^n (-1)^{i + j} A_{i j} C\left(P(i \mid j)\right) = a \cdot \sum_{i = 1}^n (-1)^{i + j} A_{i j} C\left(Q(i \mid j)\right) + \sum_{i = 1}^n (-1)^{i + j} A_{i j} C\left(R(i \mid j)\right)$$

I'm going to show that the $i^{\rm th}$ term in the sum on the left equals the sum of the $i^{\rm th}$ terms of the sums on the right. To to this, I will consider two cases: $i \ne k$ and $i = k$ .

First, consider a term in the cofactor sum where $i \ne k$ --- that is, where the row that is deleted is not the $k^{\rm th}$ row. The $i^{\rm th}$ row and $j^{\rm th}$ column are deleted from each matrix, as shown in gray in the picture below. Since C is a determinant function, I can apply linearity to the $a x + y$ row, and I get the following equation:

$$\hbox{\epsfysize=1in \epsffile{expansion-by-cofactors-2.eps}}$$

The matrices in this picture are, from left to right, $P(i \mid j)$ , $Q(i \mid j)$ , and $R(i \mid j)$ . The matrices are the same except in the $k^{\rm th}$ row (the one with the x's and y's).

Thus, the terms of the summation on the two sides agree for $i \ne k$ :

$$(-1)^{i + j} A_{i j} C\left(P(i \mid j)\right) = a \cdot (-1)^{i + j} A_{i j} C\left(Q(i \mid j)\right) + (-1)^{i + j} A_{i j} C\left(R(i \mid j)\right)$$

Next, consider the case where $i = k$ , so the row that is deleted is the $k^{\rm th}$ row. Now P, Q, and R only differ in row k, which is the row which is deleted.

$$\hbox{\epsfysize=1in \epsffile{expansion-by-cofactors-3.eps}}$$

Once it's deleted, the resulting matrices are the same:

$$C\left(P(k \mid j)\right) = C\left(Q(k \mid j)\right) = C\left(R(k \mid j)\right).$$

Therefore,

$$(-1)^{k + j} (a x_j + y_j) C\left(P(k \mid j)\right) = (-1)^{k + j} a x_j C\left(Q(k \mid j)\right) + (-1)^{k + j} y_j C\left(R(k \mid j)\right).$$

Thus, the terms on the left and right are the same for all i, and D is linear.

Alternating: I have to show that if two rows of A are the same, then $D(A) = 0$ .

First, I'll show that if rows 1 and 2 are equal, then $D(A) = 0$ .

Suppose then that rows 1 and 2 are equal. Here's a typical term in the cofactor expansion:

$$(-1)^{i + j} A_{i j} C\left(A(i \mid j)\right).$$

Suppose row i, the row that is deleted, is a row other than row 1 or row 2.

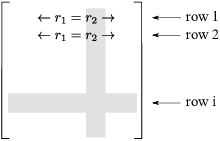
$$\hbox{\epsfysize=1.25in \epsffile{expansion-by-cofactors-4.eps}}$$

Then the matrix that results after deletion will have two equal rows, since row 1 and row 2 were equal. Therefore, $C\left(A(i \mid j)\right) = 0$ , and the term in the cofactor expansion is 0.

Thus, all the terms in the cofactor expansion are 0 except the first and second ($i = 1$ and $i = 2$ ). These terms are

$$(-1)^{1 + j} A_{1 j} C\left(A(1 \mid j)\right) + (-1)^{2 + j} A_{2 j} C\left(A(2 \mid j)\right).$$

Now $A_{1 j} = A_{2 j}$ , since the first and second rows are equal. And since row 1 and row 2 are equal, I get the same matrix by deleting either row 1 or row 2:

$$\hbox{\epsfysize=1in \epsffile{expansion-by-cofactors-5.eps}}$$

That is, $A(1 \mid j) = A(2 \mid j)$ . Therefore, $C\left(A(1 \mid j)\right) = C\left(A(2 \mid j)\right)$ .

Thus, the only way in which the two terms above differ is in the signs $(-1)^{1 + j}$ and $(-1)^{2 + j}$ . But $1 + j$ and $2 + j$ are consecutive integers, so one must be even and the other must be odd. Hence, $(-1)^{1 + j}$ and $(-1)^{2 + j}$ are either $+1$ and -1 or -1 and $+1$ . In either case, the terms cancel, and the sum of the two terms is 0.

Hence, the cofactor expansion is equal to 0, and $D(A) = 0$ , as I wished to prove.

Tou can give a similar argument if A has two adjacent rows equal other than rows 1 and 2 (so, for instance, if rows 4 and 5 are equal). I will skip the details.

Thus, I know that $D(A) = 0$ if two adjacent rows of A are equal. Since I proved that D satisfies the linearity axiom, the hypotheses of the previous technical lemma are satisfied, and I can apply it. It says that swapping two rows multiplies the determinant by -1.

Now take the general case: Two rows of A are equal, but they aren't necessarily adjacent.

I can swap the rows of A until the two equal rows are adjacent, and each swap multiplies the value of the determinant by -1. Let's say that k swaps are needed to get the two equal rows to be adjacent. That is, after k row swaps, I get a matrix B which has adjacent equal rows. Then $D(B) = 0$ by the adjacent row case above, so

$$D(A) = (-1)^k D(B) = (-1)^k \cdot 0 = 0.$$

This completes the proof that $D(A) = 0$ if A has two equal rows, and the Alternating Axiom has been verified.

The identity has determinant 1: Suppose $A = I$ . Since the entries of the identity matrix are 0 except on the main diagonal, I have $A_{i j} = 0$ unless $i = j$ . When $i = j$ , I have $A_{j j} = 1$ . Therefore, the cofactor expansion of $D(A)$ has only one nonzero term, which is

$$(-1)^{j + j} A_{j j} C\left(A(j \mid j)\right) = 1 \cdot 1 \cdot C(I) = 1.$$

(I know $C(I) = 1$ because C is a determinant function.)

I've verified that D satisfies the 3 axioms. Thus, D is a determinant function.

The theorem says that if I have a determinant function on matrices of a given size, I can use it to construct a determinant function on matrices "one size bigger". So a determinant function on $10 \times 10$ matrices can be used to construct a determinant function on $11 \times 11$ matrices, and so on.

Corollary. Let R be a commutative ring with identity. There is a determinant function on $n \times n$ matrices over R for $n \ge 1$ .

Proof. I constructed a determinant function on $1 \times 1$ and on $2 \times 2$ matrices. So applying the theorem, from the $2 \times 2$ determinant function I get a $3 \times 3$ determinant function, from the $3 \times 3$ determinant function I get a $4 \times 4$ determinant function, and so on. By induction, I get a determinant function on $n \times n$ matrices for all $n \ge 1$ .

I now know that there is at least one determinant function on $n \times n$ matrices. In fact, there is only one, but that will require a separate discussion. Anticipating that result, I'll refer to the determinant function (rather than a determinant function).

Since we'll prove that there's only one determinant function, if A is an $n \times n$ matrix, the determinant of A will be denoted $|A|$ or $\det A$ .

I'll show later on that $\det A = \det A^T$ . Since transposing sends rows to columns and columns to rows, this means that you can expand by cofactors of rows as well as columns. We'll use this result now in computations.

While you can expand along any row or column you want, but it's usually good to pick one with lots of 0's.

Example. ( Computing a determinant by cofactors) Compute the determinant of the following real matrix:

$$\left[\matrix{1 & 3 & -5 \cr 1 & 0 & -2 \cr 6 & 1 & 1 \cr}\right]$$

Expanding by cofactors of the second column, I get

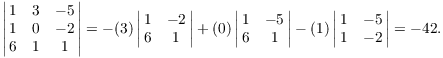
$$\left|\matrix{1 & 3 & -5 \cr 1 & 0 & -2 \cr 6 & 1 & 1 \cr}\right| = -(3) \left|\matrix{1 & -2 \cr 6 & 1 \cr}\right| + (0) \left|\matrix{1 & -5 \cr 6 & 1 \cr}\right| - (1) \left|\matrix{1 & -5 \cr 1 & -2 \cr}\right| = -42.$$

This diagram shows where the terms in the cofactor expansion come from:

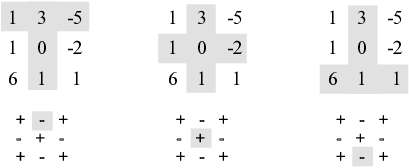
$$\hbox{\epsfysize=1.5in \epsffile{expansion-by-cofactors-6.eps}}$$

For each element (3, 0, 1) in the second column, compute the cofactor for that element by crossing out the row and column containing the element (cross-outs shown in gray), computing the determinant of the $2 \times 2$ matrix that is left, and multiplying by the sign (+ or -) that comes from the "checkerboard pattern"). Then multiply the cofactor by the column element.

So for the first term, the element is 3, the sign is "-", and after crossing out the first row and second column, the $2 \times 2$ determinant that is left is

$$\left|\matrix{1 & -2 \cr 6 & 1 \cr}\right|.$$

As usual, this is harder to describe in words than it is to actually do. Try a few computations yourself.

Finally, I computed the $2 \times 2$ determinants using the $2 \times 2$ determinant formula I derived earlier.

You can often simplify a cofactor expansion by doing row operations first. For instance, if you can produce a row or a column with lots of zeros, you can expand by cofactors of that row or column.

Example. ( Computing a determinant using row operations and cofactors) Compute the determinant of the following matrix in $M(3, \integer_3)$ :

$$\left[\matrix{1 & 2 & 1 \cr 2 & 2 & 1 \cr 2 & 0 & 1 \cr}\right]$$

I'll do a couple of row operations first to make some zeros in the first column. Remember that adding a multiple of a row to another row does not change the determinant.

$$\left|\matrix{1 & 2 & 1 \cr 2 & 2 & 1 \cr 2 & 0 & 1 \cr}\right| \matrix{\to \cr r_2 \to r_2 + r_1 \cr} \left|\matrix{1 & 2 & 1 \cr 0 & 1 & 2 \cr 2 & 0 & 1 \cr}\right| \matrix{\to \cr r_2 \to r_2 + r_1 \cr} \left|\matrix{1 & 2 & 1 \cr 0 & 1 & 2 \cr 0 & 2 & 2 \cr}\right|.$$

Now I expand by cofactors of column 1. The two zeros make the computation easy; I'll write out those terms just so you can see the cofactors:

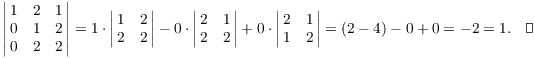
$$\left|\matrix{1 & 2 & 1 \cr 0 & 1 & 2 \cr 0 & 2 & 2 \cr}\right| = 1 \cdot \left|\matrix{1 & 2 \cr 2 & 2 \cr}\right| - 0 \cdot \left|\matrix{2 & 1 \cr 2 & 2 \cr}\right| + 0 \cdot \left|\matrix{2 & 1 \cr 1 & 2 \cr}\right| = (2 - 4) - 0 + 0 = -2 = 1.\quad\halmos$$

Contact information

Bruce Ikenaga's Home Page

Copyright 2021 by Bruce Ikenaga