Functions

In this section, I'll collect some results and terminology connected with functions. I'll assume that you have some experience with functions from earlier courses, and I won't give a formal definition of "function".

If X and Y are sets, the notation $f: X \to Y$ denotes a function named "f" which takes its inputs from the sets X and produces outputs in the set Y. The set X is callled the domain and the set Y is called the codomain.

What I just described is notation for functions; I'm not giving a precise definition of what a function is. You've seen functions in other courses --- calculus, for instance. You were probably told at some point that a function is a "rule" for producing outputs from inputs, and this intuitive idea is okay for this course. However, if you're someone who likes causing trouble for yourself, you can do so here by asking what a "rule" is: It's not so easy to say in a precise way. I'll give a quick description of the solution, and let you read more in a book on set theory or math proof if you're interested. A function from a set X to a set Y is a subset of the product $X \times Y$ , such that if $(x, y_1)$ and $(x, y_2)$ are in the subset, then $y_1 = y_2$ . For this course, you do not need to understand the last sentence!

The sets X and Y are part of the definition of the function. In some elementary courses, all the functions take real numbers (or at least some real numbers) to real numbers, and the domain and codomain are "understood". The "domain" (or natural domain, as it is sometimes called) is the largest set of real numbers for which the expression defining the function is defined. In such a course, for example, the "domain" of $f(x) = \dfrac{1}{x - 1}$ would be all real numbers except for 1.

In this course, however, we'll be careful and specify the domain and codomain explicitly. This becomes important, for instance, in defining injective and surjective functions.

If $f: X \to Y$ is a function, the image of f (denoted $\im f$ ) is the set of all possible outputs of f. In terms of set notation,

$$\im f = \{y \in Y \mid y = f(x) \quad\hbox{for some}\quad x \in X\}.$$

Notice that the image of f is contained in the codomain Y, but it can be smaller than Y.

$$\hbox{\epsfysize=1.5in \epsffile{functions-1.eps}}$$

You might have heard the term range used in connection with functions, but we'll avoid it because it was (unfortunately) used in two different ways. Sometimes, it meant what I've called the codomain, but it was also used to refer to what is now called the image. The codomain is simply a set which contains all possible outputs of the function (the image), but not every element of the codomain must be an output of the function.

Remark. (a) When you write the definition of a function like "$f(x) = x^2 + 1$ ", you can use whatever variable you wish for the input. It would be the same to write "$f(t) = t^2 + 1$ ". You could use a word for the input to the function (as is often done in compute programming) and write

$$f(\hbox{input}) = \hbox{input}^2 + 1.$$

You could even use words for the whole definition: "The function f is defined by taking an input, squaring it, and adding 1, and returning the result as the output." This is the way math was written before people started using symbols --- and you can see why people started using symbols!

In math, unlike in computer programming, it has been traditional to save writing and use single letters to name variables, such as the variables used to define functions. There are also some loose conventions about what letters you use for various purposes. For instance, x is often used as the input variable in a function definition, and i, j, and k are often used as index variables in summations.

(b) The variables used to define a function are only "active" within the function definition. Once you reach the end of the expression "$f(x) = x^2 + 1$ ", there is no variable named "x" hanging around --- you can't ask at that point "Is x equal to 3?" In computer programming terms, you might say that x isn't a global variable; it's in scope only within the definition "$f(x) = x^2 + 1$ ".

You might think about the last paragraph if you start getting confused when we discuss composites and inverse functions below.

Here are three key properties that a function may have.

Definition. Let $f: X \to Y$ be a function with domain X and codomain Y.

(a) f is injective if $f(a) = f(b)$ implies $a = b$ for $a, b \in X$ .

(b) f is surjective if for all $y \in Y$ , there is an $x \in X$ such that $f(x) = y$ .

(c) f is bijective if it is injective and surjective.

The older terms (which some people still use) are one-to-one instead of injective, onto instead of surjective, and one-to-one correspondence for bijective.

Remark. You can restate the definition of injective this way: f is injective if $a \ne b$ implies $f(a) \ne f(b)$ for $a, b \in X$ . (This is the contrapositive of the original definition.) In this form, the definition says that different inputs always give different outputs.

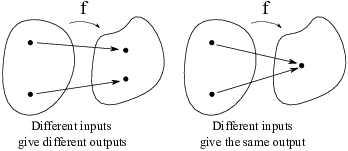
$$\hbox{\epsfysize=1.35in \epsffile{functions-2.eps}}$$

If different inputs can give the same output, the function is not injective.

The definition of surjective means that everything in the codomain is an output of f --- that is, $\im f = Y$ .

$$\hbox{\epsfysize=1.5in \epsffile{functions-3.eps}}$$

If $\im f$ is smaller than y, so some points in Y aren't in $\im f$ , the function is not surjective.

To say that f is bijective means that f "pairs up" the elements of X and the elements of Y --- one element of X paired with exactly one element of Y.

This picture shows a bijection f from the set $\{1, 2, 3\}$ to the set $\{a, b, c\}$ .

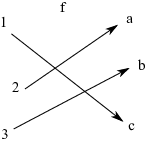
$$\hbox{\epsfysize=1.25in \epsffile{functions-4.eps}}$$

It is defined by

$$f(1) = c, \quad f(2) = a, \quad f(3) = b.$$

It is injective because two different inputs always produce two different outputs. It is surjective because every element of the codomain $\{a, b, c\}$ is an output of f.

Example. (a) $f: \real \to \real$ is defined by $f(x) = e^x$ . Prove that f is injective but not surjective.

(b) $f: \real \to \real$ is defined by

$$f(x) = \cases{ x + 1 & if $x \le 0$ \cr x & if $x > 0$ \cr}.$$

Prove that f is surjective but not injective.

(c) $f: \real \to \real$ is defined by $f(x) = x^3 + 13$ . Prove that f is bijective.

(a) Suppose $f(a) = f(b)$ . Then $e^a = e^b$ , so $\ln e^a = \ln e^b$ , and hence $a = b$ . Thus, f is injective.

f is not surjective, because there is no $x \in \real$ such that $f(x) = -5$ . This would imply $e^x = -5$ , but $e^x$ is positive for all x.

(b) Let $y \in \real$ . If $y \le 0$ , then $y - 1 \le -1$ . Hence, $f(y - 1) = (y - 1) + 1 = y$ . If $y > 0$ , then $f(y) = y$ . In both cases, I've found an input to f which produces the output y. So f is surjective.

f is not injective: $f(0) = 0 + 1 = 1$ , and $f(1) = 1$ , so $f(0) = f(1)$ but $0 \ne 1$ .

The graph of f is shown below.

$$\hbox{\epsfysize=1.75in \epsffile{functions-5.eps}}$$

In the case of functions $\real \to \real$ , you can interpret surjectivity this way: Every horizontal line hits the graph at least once. You can interpret injectivity this way: No horizontal line hits the graph more than once. Look at the graph and see how it shows that f is surjective, but not injective.

While this is visually appealing, this is a special case --- do not remember these ideas as the definitions of injective and surjective. For instance, they would not apply if you had a function $\real^2 \to \real^3$ .

(c) Suppose $f(a) = f(b)$ . Then

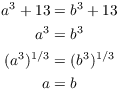
$$\eqalign{ a^3 + 13 & = b^3 + 13 \cr a^3 & = b^3 \cr (a^3)^{1/3} & = (b^3)^{1/3} \cr a & = b \cr}$$

Hence, f is injective.

Suppose $y \in \real$ . I need $x \in \real$ such that $f(x) = y$ . I will work backwards to "guess" what x should be, then verify my guess.

$f(x) = y$ means $x^3 + 13 = y$ , so $x^3 = y - 13$ , and $x = (y - 13)^{1/3}$ . That's my "guess" for x; I still have to show it works. (Why doesn't what I did prove it? Because I worked backwards, so I have to check that all the steps I took are reversible.) Here's the check:

$$f((y - 13)^{1/3}) = [(y - 13)^{1/3}]^3 + 13 = y - 13 + 13 = y.$$

Hence, f is surjective. Since f is injective and surjective, it's bijective.

Example. $f: \real^2 \to \real^2$ is defined by

$$f(x, y) = (x^3 + 2, x + e^y).$$

Show that f is injective, but not surjective.

To show f is injective, suppose $f(a, b) = f(c, d)$ . Then

$$(a^3 + 2, a + e^b) = (c^3 + 2, c + e^d).$$

Equating the first components, I have

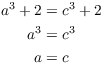
$$\eqalign{ a^3 + 2 & = c^3 + 2 \cr a^3 & = c^3 \cr a & = c \cr}$$

Equating the second components and using $a = c$ , I have

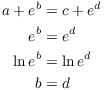
$$\eqalign{ a + e^b & = c + e^d \cr e^b & = e^d \cr \ln e^b & = \ln e^d \cr b & = d \cr}$$

Hence, $(a, b) = (c, d)$ , so f is injective.

To show f is not surjective, I must find a pair in $\real^2$ which is not an output of f. There are lots of pairs which work; I will use $(10, 0)$ . So suppose $f(x, y) = (10, 0)$ . Then

$$(x^3 + 2, x + e^y) = (10, 0).$$

Equating the first components, I have

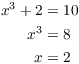
$$\eqalign{ x^3 + 2 & = 10 \cr x^3 & = 8 \cr x & = 2 \cr}$$

Equating the second components and using $x = 2$ , I have

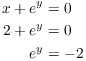
$$\eqalign{ x + e^y & = 0 \cr 2 + e^y & = 0 \cr e^y & = -2 \cr}$$

This is a contradiction, since $e^y > 0$ for all y. So there is no input $(x, y)$ such that $f(x, y) = (10, 0)$ , and hence f is not surjective.

The thought process I used in choosing $(10, 0)$ was this. I saw that the expression $e^y$ was restricted in the values it can take: It's always positive. So I tried to get a contradiction by forcing it to equal a negative number. I could do this by forcing x in $x + e^y$ to be positive. I could force $x > 0$ by setting the first component $x^3 + 2$ to a value so that solving for x would produce a positive number --- 10 happens to work.

Definition. Let X, Y, and Z be sets, and let $f: X \to Y$ and $g: Y \to Z$ be functions. The composite of f and g is the function $g \circ f: X \to Z$ defined by

$$(g \circ f)(x) = g(f(x)).$$

$$\hbox{\epsfysize=1.5in \epsffile{functions-6.eps}}$$

Note that "$g \circ f$ " does not mean multiplication. I will often write "$g(f(x))$ " for the composite, to ensure that there's no confusion. Also, "$g \circ f$ " is read from right to left, so it means "do f first, then g".

Example. (a) Suppose $f: \real \to \real$ is defined by $f(x) = x^2$ and $g: \real \to \real$ is defined by $g(x) = x + 2$ . Find $g(f(x))$ , $f(g(x))$ , $g(g(x))$ , and $f(f(3))$ .

(b) Suppose $f: \real \to \real^2$ is given by $f(x) = (x + 3, e^x)$ and $g: \real^2 \to \real$ is given by $g(s, t) = s - t$ . Find $g(f(x))$ and $f(g(s, t))$ .

(c) Suppose $f: \real^2 \to \real^2$ is given by $f(x, y) = (x + 3 y, 2 x - y)$ and $g(s, t) = (s t, s + t)$ . Find $g(f(x, y))$ and $f(g(s, t))$ .

(a)

$$g(f(x)) = g(x^2) = x^2 + 2.$$

$$f(g(x)) = f(x + 2) = (x + 2)^2.$$

$$g(g(x)) = g(x + 2) = (x + 2) + 2 = x + 4.$$

$$f(f(3)) = f(3^2) = f(9) = 9^2 = 81.$$

Note that $g(f(x)) \ne f(g(x))$ .

(b)

$$g(f(x)) = g(x + 3, e^x) = x + 3 - e^x.$$

$$f(g(s, t)) = f(s - t) = ((s - t) + 3, e^{s - t}).\quad\halmos$$

(c)

$$g(f(x, y)) = g(x + 3 y, 2 x - y) = ((x + 3 y)(2 x - y), (x + 3 y) + (2 x - y)) = ((x + 3 y)(2 x - y), 3 x + 2 y).$$

$$f(g(s, t)) = f(s t, s + t) = (s t + 3(s + t), 2 s t - (s + t)).$$

For example, to compute $g(x + 3 y, 2 x - y)$ , I substituted $x + 3 y$ for s and $2 x - y$ for t in the definition of $g(s, t)$ .

Definition. Let A and B be sets, and let $f: A \to B$ and $g: B \to A$ be functions. f and g are inverses if

$$f(g(b)) = b \quad\hbox{for all}\quad b \in B \quad\hbox{and}\quad g(f(a)) = a \quad\hbox{for all}\quad a \in A.$$

The inverse of f is denoted $f^{-1}$ . (Note that "$f^{-1}$ " is not a "-1 power", in the sense of a reciprocal.) Using this notation, I can write the equations in the inverse definition as

$$f(f^{-1}(b)) = b \quad\hbox{for all}\quad b \in B \quad\hbox{and}\quad f^{-1}(f(a)) = a \quad\hbox{for all}\quad a \in A.$$

The identity function on a set X is the function $\id_X$ defined by $\id_X(x) = x$ for all $x \in X$ . We may write "$\id$ " instead of "$\id_X$ " if it's clear what set is intended.

Using this definition and the notation for the composite of functions, we can write the two equations which say that f and g are inverses as

$$f \circ f = \id_B \quad\hbox{and}\quad g \circ f = \id_A.$$

Example. Define $f: \real \to \real$ by $f(x) = x^3 + 7$ and $g: \real \to \real$ by $g(x) = (x - 7)^{1/3}$ . Show that f and g are inverses.

Let $x \in \real$ .

$$f(g(x)) = f((x - 7)^{1/3}) = [(x - 7)^{1/3}]^3 + 7 = x - 7 + 7 = x.$$

$$g(f(x)) = g(x^3 + 7) = [(x^3 + 7) - 7]^{1/3} = (x^3)^{1/3} = x.$$

Since $f(g(x)) = x$ and $g(f(x)) = x$ for all $x \in \real$ , it follows that f and g are inverses.

Example. Let $f: \real \to \real$ be given by $f(x) = 10 - x^{1/5}$ . Find $f^{-1}$ and verify that it's the inverse by checking the inverse definition.

I guess $f^{-1}$ by working backwards. Suppose $f^{-1}(y) = x$ . Then

$$f(f^{-1}(y)) = f(x), \quad\hbox{so}\quad y = f(x) = 10 - x^{1/5}.$$

Solve the last equation for x:

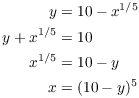
$$\eqalign{ y & = 10 - x^{1/5} \cr y + x^{1/5} & = 10 \cr x^{1/5} & = 10 - y \cr x & = (10 - y)^5 \cr}$$

Thus, my guess is $f^{-1}(y) = x = (10 - y)^5$ . I got this by assuming $f^{-1}(y) = x$ . I need to verify that my guess works by checking the inverse definition.

$$f(f^{-1}(y)) = f((10 - y)^5) = 10 - [(10 - y)^5]^{1/5} = 10 - (10 - y) = y.$$

$$f^{-1}(f(x)) = f^{-1}(10 - x^{1/5}) = [10 - (10 - x^{1/5})]^5 = (x^{1/5})^5 = x.$$

Since $f(f^{-1}(y)) = y$ for all $y \in \real$ and $f^{-1}(f(x)) = x$ for all $x \in \real$ , it follows that $f^{-1}(y) = (10 - y)^5$ is the inverse function of f.

Note: While I needed to use different letters x and y for the output and input variables for $f^{-1}$ , you can use any variable you want in writing the definition of a function. So once I have my guess for $f^{-1}$ , I could have written the definition as $f^{-1}(x) = (10 - x)^5$ and checked the inverse definition using that.

Not every function has an inverse --- in fact, we'll see below that having an inverse is equivalent to being bijective.

Example. Define $f: \real \to \real$ by $f(x) = x^2 + 10$ . Prove that f does not have an inverse.

If you have some experience with proof writing, you may know that a negative statement ("does not have an inverse") is often proved by contradiction: You assume the negation of the statement to be proved and try to get a contradiction. If the statement to be proved is a negative statement, its negation will be a positive statement.

So suppose that f has an inverse $f^{-1}$ . Then $f^{-1}(f(x)) = x$ for all x. In particular, $f^{-1}(f(2)) = 2$ and $f^{-1}(f(-2)) = -2$ . But $f(2) = 14$ and $f(-2) = 14$ , so I get

$$f^{-1}(14) = 2 \quad\hbox{and}\quad f^{-1}(14) = -2.$$

This is a contradiction, because $f^{-1}$ is a function, so it can't produce two different outputs (2 and -2) for the same input (14). Hence, f does not have an inverse.

Note: Instead of 2 and -2, you could choose 5 and -5 or 17 and -17, and so on. Lots of pairs of numbers would work. You could also get a contradiction using the equation $f(f^{-1}(x)) = x$ : Take $x = 6$ and see what happens!

Example. Let $f: \real^2 \to \real^2$ be given by $f(x, y) = (x^{1/3} - 4, -x + y)$ . Find $f^{-1}$ and verify that it's the inverse by checking the inverse definition.

I'll guess $f^{-1}$ by working backwards, then verify that my guess works. Suppose $f^{-1}(a, b) = (x, y)$ . Then

$$f(f^{-1}(a, b)) = f(x, y), \quad\hbox{so}\quad (a, b) = f(x, y) = (x^{1/3} - 4, -x + y).$$

The second equality gives two equations:

$$a = x^{1/3} - 4, \quad b = -x + y.$$

The first equation gives $x^{1/3} = a + 4$ , so $x = (a + 4)^3$ . Plugging this into the second equation gives

$$b = -(a + 4)^3 + y, \quad\hbox{so}\quad y = (a + 4)^3 + b.$$

Thus, my guess is

$$f^{-1}(a, b) = (x, y) = ((a + 4)^3, (a + 4)^3 + b).$$

I check the inverse definition:

$$f(f^{-1}(a, b)) = f((a + 4)^3, (a + 4)^3 + b) = ([(a + 4)^3]^{1/3} - 4, -(a + 4)^3 + (a + 4)^3 + b) =$$

$$(a + 4 - 4, b) = (a, b).$$

$$f^{-1}(f(x, y)) = f^{-1}(x^{1/3} - 4, -x + y) = ([(x^{1/3} - 4) + 4]^3, [(x^{1/3} - 4) + 4]^3 + (-x + y)) = ((x^{1/3})^3, (x^{1/3})^3 - x + y) =$$

$$(x, x - x + y) = (x, y).$$

The inverse definition checks, so $f^{-1}(a, b) = (x, y) = ((a + 4)^3, (a + 4)^3 + b)$ .

Note: While the names of the input variables to a function are arbitrary, I used a and b as the input variables to $f^{-1}$ rather than x and y to avoid confusion --- I was already using x and y as the input variables for f.

The next result says that having an inverse is the same as being bijective.

Theorem. Let X and Y be sets, and let $f: X \to Y$ be a function. f is bijective if and only if it has an inverse --- that is, $f^{-1}$ exists.

Proof. To prove a statement of the form A if and only if B, I must do two things: First, I assume that A is true and prove that B is true; next, I assume that B is true and prove that A is true.

First, suppose that $f^{-1}$ exists, so

$$f(f^{-1}(y)) = y \quad\hbox{for all}\quad y \in Y \quad\hbox{and}\quad f^{-1}(f(x)) = x \quad\hbox{for all}\quad x \in X.$$

I need to prove that f is bijective.

To show that f is injective, suppose that $f(x_1) = f(x_2)$ for $x_1, x_2 \in X$ . Then

$$f^{-1}(f(x_1)) = f^{-1}(f(x_2)), \quad\hbox{so}\quad x_1 = x_2.$$

Therefore, f is injective.

To show f is surjective, suppose $y \in Y$ . I must find an element of X which f maps to y. This is easy, since $f^{-1}(y) \in X$ , and

$$f(f^{-1}(y)) = y.$$

Therefore, f is surjective. Hence, f is bijective.

Next, suppose f is bijective. I must show that $f^{-1}$ exists. Now $f^{-1}$ should be a function from Y to X, so I need to start with $y \in Y$ and define where $f^{-1}$ maps it. Since f is bijective, it is surjective. Therefore, $f(x) = y$ for some $x \in X$ . I'd like to define $f^{-1}(y) = x$ .

There's a possible problem. In general, it's possible that $f(x_1) = y$ and $f(x_2) = y$ for $x_1, x_2 \in X$ . In that case, how would I define $f^{-1}(y)$ ?

Fortunately, f is injective. So if $f(x_1) = y$ and $f(x_2) = y$ , then $f(x_1) = f(x_2)$ , and so $x_1 = x_2$ by injectivity. In other words, there is one and only one $x \in X$ such that $f(x) = y$ , and it's safe for me to define $f^{-1}(y) = x$ .

(Notice how I used both parts of the definition of bijective --- surjectivity and injectivity --- to define $f^{-1}$ .)

All I have to do is to check the inverse definition. First, if $x \in X$ , then by definition $f^{-1}(f(x))$ is the element of X which f takes to $f(x)$ --- but that element is x. Hence, $f^{-1}(f(x)) = x$ .

Next, if $y \in Y$ , then by definition $f^{-1}(y)$ is the element $x \in X$ such that $f(x) = y$ . So

$$f^{-1}(y) = x \quad\hbox{and}\quad f(f^{-1}(y)) = f(x) = y.$$

Thus, the function $f^{-1}$ I've defined really is the inverse of f.

Thus, to show a function is bijective, you just need to show the function has an inverse. Often this is easy, because you can tell what the inverse should be given the function's definition. All you have to do is check that the "obvious" inverse really is the inverse.

For instance, if $f: \real \to \real$ is defined by $f(x) = x^3$ , it's obvious that the opposite of "cubing" is "cube rooting". So I expect the inverse to be $f^{-1}(x) = x^{1/3}$ . The check is easy:

$$f(f^{-1}(x)) = f(x^{1/3}) = (x^{1/3})^3 = x \quad\hbox{and}\quad f^{-1}(f(x)) = f^{-1}(x^3) = (x^3)^{1/3} = x.$$

Since f has an inverse, it's bijective.

Contact information

Bruce Ikenaga's Home Page

Copyright 2022 by Bruce Ikenaga