Inverses and Elementary Matrices

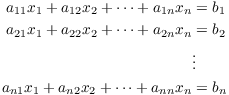
Matrix inversion gives a method for solving some systems of equations. Suppose we have a system of n linear equations in n variables:

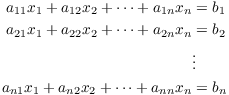
$\eqalign{a_{11}x_1 + a_{12}x_2 + \cdots + a_{1n}x_n &= b_1 \cr a_{21}x_1 + a_{22}x_2 + \cdots + a_{2n}x_n &= b_2 \cr & \vdots \cr a_{n1}x_1 + a_{n2}x_2 + \cdots + a_{nn}x_n &= b_n \cr}$

Let

$A = \left[\matrix{a_{11} & a_{12} & \ldots & a_{1n} \cr a_{21} & a_{22} & \ldots & a_{2n} \cr \vdots & \vdots & \ddots & \vdots \cr a_{n1} & a_{n2} & \ldots & a_{nn} \cr}\right], \quad x = \left[\matrix{x_1 \cr x_2 \cr \vdots \cr x_n \cr}\right], \quad b = \left[\matrix{b_1 \cr b_2 \cr \vdots \cr b_n \cr}\right].$

The system can then be written in matrix form:

(One reason for using matrix notation is that it saves writing!) If A has an inverse $A^{-1}$ , I can multiply both sides by $A^{-1}$ :

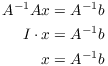
$\eqalign{A^{-1} A x &= A^{-1} b \cr I \cdot x &= A^{-1} b \cr x & = A^{-1} b \cr}$

I've solved for the vector x of variables.

Not every matrix has an inverse --- an obvious example is the zero matrix, but here's a nonzero non-invertible matrix over the real numbers:

$\left[\matrix{ 1 & 1 \cr 0 & 0 \cr}\right].$

Suppose this matrix had an inverse $\displaystyle \left[\matrix{a & b \cr c & d \cr}\right]$ . Then

$\left[\matrix{ 1 & 1 \cr 0 & 0 \cr}\right] \left[\matrix{ a & b \cr c & d \cr}\right] = \left[\matrix{ 1 & 0 \cr 0 & 1 \cr}\right], \quad\hbox{so}\quad \left[\matrix{ a + c & b + d \cr 0 & 0 \cr}\right] = \left[\matrix{ 1 & 0 \cr 0 & 1 \cr}\right].$

But equating entries in row 2, column 2 gives the contradiction . Hence, the original matrix does not have an inverse.

If we want to know whether a matrix has an inverse, we could try to do what we did in this example --- set up equations and see if we can solve them. But you can see that it could be pretty tedious if the matrix was large or the entries were messy. And we saw earlier that you can solve systems of linear equations using row reduction.

In this section, we'll see how you can use row reduction to determine whether a matrix has an inverse --- and, if it does, how to find the inverse. We'll begin by explaining the connection between elementary row operations and matrices.

Definition. An elementary matrix is a matrix which represents an elementary row operation. "Represents" means that multiplying on the left by the elementary matrix performs the row operation.

Here are the elementary matrices that represent our three types of row operations. In the pictures below, the elements that are not shown are the same as those in the identity matrix. In particular, all of the elements that are not on the main diagonal are 0, and all the main diagonal entries --- except those shown --- are 1.

Multiplying by this matrix swaps rows i and j:

$\bordermatrix{ & & & & i & & j & & & \cr & 1 & 0 & & & & & & & \cr & 0 & 1 & & & & & & & \cr & & & \ddots & & & & & & \cr i & & & & 0 & \cdots & 1 & & & \cr & & & & \vdots & & \vdots & & & \cr j & & & & 1 & \cdots & 0 & & & \cr & & & & & & & \ddots & & \cr & & & & & & & & 1 & 0 \cr & & & & & & & & 0 & 1 \cr}$

The "i" and "j" on the borders of the matrix label rows and columns so you can see where the elements are.

This is the same as the identity matrix, except that rows i and j have been swapped. In fact, you obtain this matrix by applying the row operation ("swap rows i and j") to the identity matrix. This is true for our other elementary matrices.

Multiplying by this matrix multiplies row i by the number c:

$\bordermatrix{ & & & & i & & & \cr & 1 & 0 & & & & & \cr & 0 & 1 & & & & & \cr & & & \ddots & & & & \cr i & & & & c & & & \cr & & & & & \ddots & & \cr & & & & & & 1 & 0 \cr & & & & & & 0 & 1 \cr}$

This is the same as the identity matrix, except that row i has been multiplied by c. Note that this is only a valid operation if the number c has a multiplicative inverse. For instance, if we're working over the real numbers, c can be any nonzero number.

Multiplying by this matrix replaces row i with row i plus c times row j.

$\bordermatrix{ & & & & i & & j & & & \cr & 1 & 0 & & & & & & & \cr & 0 & 1 & & & & & & & \cr & & & \ddots & & & & & & \cr i & & & & 1 & \cdots & c & & & \cr & & & & \vdots & & \vdots & & & \cr j & & & & 0 & \cdots & 1 & & & \cr & & & & & & & \ddots & & \cr & & & & & & & & 1 & 0 \cr & & & & & & & & 0 & 1 \cr}$

To get this matrix, apply the operation "add c times row j to row i" to the identity matrix.

While we could give formal proofs that these matrices do what we want --- we would have to write formulas for elements of the matrices, then use the definition of matrix multiplication --- I don't think the proofs would be very enlightening. It's good, however, to visualize the multiplications for yourself to see why these matrices work: Take rows of the elementary matrix and picture them multiplying rows of the original matrix. For example, consider the elementary matrix that swaps row i and row j.

When you multiply the original matrix by row FOO of this matrix, you get row FOO of the product. So multiplying the original matrix by first row of this matrix gives the first row of the product, and so on. Let's look at what happens when you multiply the original matrix by row i of this matrix.

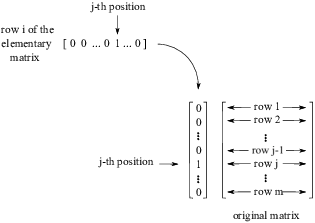
$\hbox{\epsfysize=2in \epsffile{inverses-and-elementary-matrices-1.eps}}$

Row i has 0's everywhere except for a 1 in the $j^{\rm th}$ position. So when it multiplies the original matrix, all the rows of the original matrix get multiplied by 0, except for the $j^{\rm th}$ row, which is multiplied by 1. The net result is the $j^{\rm th}$ row of the original matrix. Thus, the $i^{\rm th}$ row of the product is the $j^{\rm th}$ row of the original matrix.

If you picture this process one row at a time, you'll see that the original matrix is replaced with the same matrix with the i and j rows swapped.

Let's try some examples.

This elementary matrix should swap rows 2 and 3 in a $3 \times 3$ matrix:

$\left[\matrix{ 1 & 0 & 0 \cr 0 & 0 & 1 \cr 0 & 1 & 0 \cr}\right]$

Notice that it's the identity matrix with rows 2 and 3 swapped.

Multiply a $3 \times 3$ matrix by it on the left:

$\left[\matrix{ 1 & 0 & 0 \cr 0 & 0 & 1 \cr 0 & 1 & 0 \cr}\right] \left[\matrix{ a & b & c \cr d & e & f \cr g & h & i \cr}\right] = \left[\matrix{ a & b & c \cr g & h & i \cr d & e & f \cr}\right].$

Rows 2 and 3 were swapped --- it worked!

This elementary matrix should multiply row 2 of a $2 \times 2$ matrix by 13:

$\left[\matrix{ 1 & 0 \cr 0 & 13 \cr}\right]$

Notice that it's the identity matrix with row 2 multiplied by 13. (We'll assume that we're in a number system where 13 is invertible.)

Multiply a $2 \times 2$ matrix by it on the left:

$\left[\matrix{ 1 & 0 \cr 0 & 13 \cr}\right] \left[\matrix{ a & b \cr c & d \cr}\right] = \left[\matrix{ a & b \cr 13 c & 13 d \cr}\right].$

Row 2 orf the original matrix was multiplied by 13.

This elementary matrix should add 5 times row 1 to row 3:

$\left[\matrix{ 1 & 0 & 0 \cr 0 & 1 & 0 \cr 5 & 0 & 1 \cr}\right]$

Notice that it's the identity matrix with 5 times row 1 added to row 3.

Multiply a $3 \times 3$ matrix by it on the left:

$\left[\matrix{ 1 & 0 & 0 \cr 0 & 1 & 0 \cr 5 & 0 & 1 \cr}\right] \left[\matrix{ a & b & c \cr d & e & f \cr g & h & i \cr}\right] = \left[\matrix{ a & b & c \cr d & e & f \cr g + 5 a & h + 5 b & i + 5 c \cr}\right].$

You can see that 5 times row 1 was added to row 3.

The inverses of these matrices are, not surprisingly, the elementary matrices which represent the inverse row operations. The inverse of a row operation is the row operation which undoes the original row operation. Let's look at the three operations in turn.

The inverse of swapping rows i and j is swapping rows i and j --- to undo swapping two things, you swap the two things back! So the inverse of the "swap row i and j" elementary matrix the the same matrix:

The inverse of multiplying row i by c is dividing row i by c. To account for the fact that a number system might not have "division", I'll say "multiplying row i by $c^{-1}$ ". Just take the original "multiply row i by c" elementary matrix above and replace c with $c^{-1}$ :

$\bordermatrix{ & & & & i & & & \cr & 1 & 0 & & & & & \cr & 0 & 1 & & & & & \cr & & & \ddots & & & & \cr i & & & & c^{-1} & & & \cr & & & & & \ddots & & \cr & & & & & & 1 & 0 \cr & & & & & & 0 & 1 \cr}$

The inverse of adding c times row j to row i is subtracting c times row j from row i. To write down the inverse, I just replace c with in the matrix for "row i goes to row i plus c times row j":

$\bordermatrix{ & & & & i & & j & & & \cr & 1 & 0 & & & & & & & \cr & 0 & 1 & & & & & & & \cr & & & \ddots & & & & & & \cr i & & & & 1 & \cdots & -c & & & \cr & & & & \vdots & & \vdots & & & \cr j & & & & 0 & \cdots & 1 & & & \cr & & & & & & & \ddots & & \cr & & & & & & & & 1 & 0 \cr & & & & & & & & 0 & 1 \cr}$

Example. In each case, tell what row operation is performed by multiplying on the left by the elementary matrix. Then find the inverse of the elementary matrix, and tell what row operation is performed by multiplying on the left by the inverse. (All the matrices are real number matrices.)

(a) $\displaystyle \left[\matrix{1 & 0 & 2 \cr 0 & 1 & 0 \cr 0 & 0 & 1 \cr}\right]$

(b) $\displaystyle \left[\matrix{0 & 1 & 0 \cr 1 & 0 & 0 \cr 0 & 0 & 1 \cr}\right]$

(a) Multiplying on the left by

$\left[\matrix{1 & 0 & 2 \cr 0 & 1 & 0 \cr 0 & 0 & 1 \cr}\right] \quad\hbox{adds 2 times row 3 to row 1}.$

The inverse

$\left[\matrix{1 & 0 & 2 \cr 0 & 1 & 0 \cr 0 & 0 & 1 \cr}\right]^{-1} = \left[\matrix{1 & 0 & -2 \cr 0 & 1 & 0 \cr 0 & 0 & 1 \cr}\right] \quad\hbox{subtracts 2 times row 3 from row 1}.$

(b) Multiplying on the left by

$\left[\matrix{0 & 1 & 0 \cr 1 & 0 & 0 \cr 0 & 0 & 1 \cr}\right] \quad\hbox{swaps row 1 and row 2}.$

The inverse

$\left[\matrix{0 & 1 & 0 \cr 1 & 0 & 0 \cr 0 & 0 & 1 \cr}\right]^{-1} = \left[\matrix{0 & 1 & 0 \cr 1 & 0 & 0 \cr 0 & 0 & 1 \cr}\right] \quad\hbox{swaps row 1 and row 1}.$

$\left[\matrix{1 & 0 & 0 \cr 0 & 17 & 0 \cr 0 & 0 & 1 \cr}\right] \quad\hbox{multiplies row 2 by 17}.$

The inverse

$\left[\matrix{1 & 0 & 0 \cr 0 & 17 & 0 \cr 0 & 0 & 1 \cr}\right]^{-1} = \left[\matrix{1 & 0 & 0 \cr \noalign{\vskip2pt} 0 & \dfrac{1}{17} & 0 \cr \noalign{\vskip2pt} 0 & 0 & 1 \cr}\right] \quad\hbox{divides row 2 by 17}.\quad\halmos$

Definition. Matrices A and B are row equivalent if A can be transformed to B by a finite sequence of elementary row operations.

Of course, row equivalent matrices must have the same dimensions.

Remark. Since row operations may be performed by multiplying by elementary matrices, A and B are row equivalent if and only if there are elementary matrices , ..., such that

$E_1\cdots E_nA = B.$

Lemma. Row equivalence is an equivalence relation.

Proof. Let's recall what it means (in this situation) to be an equivalence relation. I have to show three things:

(a) (Reflexivity) Every matrix is row equivalent to itself.

(b) (Symmetry) If A row reduces to B, then B row reduces to A.

(a) is obvious, since I can row reduce a matrix to itself by performing the identity row operation.

For (b), suppose A row reduces to B. Then there are elementary matrices , ... such that

$E_1 \cdots E_nA = B.$

Hence,

$A = E_n^{-1} \cdots E_1^{-1} B.$

Since the inverse of an elementary matrix is an elementary matrix, each $E_i^{-1}$ is an elementary matrix. This equation gives a sequence of row operations which row reduces B to A.

To prove (c), suppose A row reduces to B and B row reduces to C. Then there are elementary matrices , ..., and , ..., such that

$E_1 \cdots E_m A = B \quad\hbox{and}\quad F_1 \cdots F_n B = C.$

Hence,

$F_1 \cdots F_n E_1 \cdots E_m A = C.$

This equation gives a sequence of row operations which row reduces A to C.

Therefore, row equivalence is an equivalence relation.

Let's recall the definition of invertibility and the inverse of a matrix.

Definition. An $n \times n$ matrix A is invertible if there is an $n \times n$ matrix B such that , where I is the $n \times n$ identity matrix.

In this case, B is the inverse of A (or A is the inverse of B), and we write $A^{-1}$ for B (or $B^{-1}$ for A).

We use the usual notation for integer powers of a square matrix.

Notation. If A is a square matrix, then

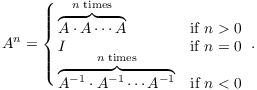
$A^n = \cases{ \overbrace{A \cdot A \cdots A}^{n\rm\;times} & if $n > 0$ \cr I & if $n = 0$ \cr \overbrace{A^{-1} \cdot A^{-1} \cdots A^{-1}}^{n\rm\;times} & if $n < 0$ \cr}.$

Note that for only makes sense if A is invertible.

The usual rules for powers hold:

(a) $A^m A^n = A^{m + n}$ .

(b) $(A^m)^n = A^{m n}$ .

The proofs involve induction and taking cases. I don't think they're that enlightening, so I will skip them.

Example. Consider the real matrix

$A = \left[\matrix{3 & 1 \cr 2 & 0 \cr}\right].$

Compute and $A^{-2}$ .

$A^2 = A \cdot A = \left[\matrix{3 & 1 \cr 2 & 0 \cr}\right] \left[\matrix{3 & 1 \cr 2 & 0 \cr}\right] = \left[\matrix{11 & 3 \cr 6 & 2 \cr}\right].$

Using the formula for the inverse of a $2 \times 2$ matrix,

$A^{-1} = \dfrac{1}{3 \cdot 0 - 2 \cdot 1} \left[\matrix{0 & -1 \cr -2 & 3}\right] = \left[\matrix{0 & 0.5 \cr 1 & -1.5 \cr}\right].$

Therefore,

$A^{-2} = A^{-1} \cdot A^{-1} = \left[\matrix{0 & 0.5 \cr 1 & -1.5 \cr}\right] \left[\matrix{0 & 0.5 \cr 1 & -1.5 \cr}\right] = \left[\matrix{0.5 & -0.75 \cr -1.5 & 2.75 \cr}\right].\quad\halmos$

Remember that matrix multiplication isn't commutative, so is not necessarily equal to . So what is ? Since is shorthand for $X \cdot X$ , and in this case , the best we can say is that

Example. Give a specific example of two $2 \times 2$ real matrices A and B for which

$(A B)^2 \ne A^2 B^2.$

How should I construct this counterexample? On the one hand, I want to avoid matrices which are "too special", because I might accidentally get a case where the equation holds. (The example in this problem just shows that the equation " " isn't always true; this doesn't mean that it's never true.) For instance, I should not take A to be the identity matrix or the zero matrix (in which case the equation would actually be true).

On the other hand, I'd like to keep the matrices simple --- first, so that I don't struggle to do the computation, and second, so that a reader can easily see that the computation works. For instance, this would be a bad idea:

$A = \left[\matrix{-1.378 & \pi \cr \noalign{\vskip2pt} \dfrac{\sqrt{2}}{171} & 1013 \cr}\right].$

When you're trying to construct a counterexample, try to keep these ideas in mind. In the end, you may have to make a few trials to get a suitable counterexample --- you will not know whether something works without trying.

I will take

$A = \left[\matrix{ 1 & 0 \cr 1 & 1 \cr}\right] \quad\hbox{and}\quad B = \left[\matrix{ 0 & 1 \cr 1 & 0 \cr}\right].$

Following the ideas above, I tried to make matrices which were simple without being too special.

Then

$A^2 = \left[\matrix{ 1 & 0 \cr 2 & 1 \cr}\right] \quad\hbox{and}\quad B^2 = \left[\matrix{ 1 & 0 \cr 0 & 1 \cr}\right] \quad\hbox{so}\quad A^2 B^2 = \left[\matrix{ 1 & 0 \cr 2 & 1 \cr}\right].$

On the other hand,

$A B = \left[\matrix{ 0 & 1 \cr 1 & 1 \cr}\right] \quad\hbox{so}\quad (A B)^2 = \left[\matrix{ 1 & 1 \cr 1 & 2 \cr}\right].$

So for these two matrices, $A^2 B^2 \ne (A B)^2$ .

Proposition.

(a) If A and B are invertible $n \times n$ matrices, then is invertible, and its inverse is given by

$(A B)^{-1} = B^{-1} A^{-1}.$

(b) If A is invertible, then is invertible, and its inverse is given by

$(A^T)^{-1} = (A^{-1})^T.$

Proof. (a) Remember that is not necessarily equal to , since matrix multiplication is not necessarily commutative.

I have

$(B^{-1} A^{-1})(A B) = B^{-1} I B = B^{-1} B = I,$

$(A B)(B^{-1} A^{-1}) = A I A^{-1} = A A^{-1} = I.$

Since $B^{-1} A^{-1}$ gives the identity when multiplied by , it means that $B^{-1}A^{-1}$ must be the inverse of --- that is, $(A B)^{-1} = B^{-1} A^{-1}$ .

(b) I have

$A^T (A^{-1})^T = \left(A^{-1} A\right)^T = I^T = I \quad\hbox{and}\quad (A^{-1})^T A^T = \left(A A^{-1}\right)^T = I^T = I.$

Since $(A^{-1})^T$ gives the identity when multiplied by , it means that $(A^{-1})^T$ must be the inverse of --- that is, $(A^T)^{-1} = (A^{-1})^T$ .

Remark. Look over the proofs of the two parts of the last proposition and be sure you understand why the computations proved the things that were to be proved. The idea is that the inverse of a matrix is defined by a property, not by appearance. By analogy, it is like the difference between the set of mathematicians (a set defined by a property) and the set of people with purple hair (a set defined by appearance).

A matrix C is the inverse of a matrix D if it has the property that multiplying C by D (in both orders) gives the identity I. So to check whether a matrix C really is the inverse of D, you multiply C by D (in both orders) any see whether you get I.

Example. Suppose that A and B are $n \times n$ invertible matrices. Simplify the following expression:

$(A B)^{-2}\,A\,(B A)^2\,A.$

Note: $(A B)^{-2}$ is not $A^{-2} B^{-2}$ , nor is it $B^{-2} A^{-2}$ .

$\eqalign{ (A B)^{-2} A (B A)^2 A & = [(A B)^2]^{-1} A (B A)^2 A \cr & = (A B A B)^{-1} A (B A B A) A \cr & = B^{-1} A^{-1} B^{-1} A^{-1} A B A B A A \cr & = A^2 \cr} \quad\halmos$

Example. ( Solving a matrix equation) Solve the following matrix equation for X, assuming that A and B are invertible:

$A^2\,X\,B\,A = A\,B.$

$\eqalign{ A^2 X B A & = A B \cr A^{-2} A^2 X B A & = A^{-2} A B \cr X B A & = A^{-1} B \cr X B A A^{-1} & = A^{-1} B A^{-1} \cr X B & = A^{-1} B A^{-1} \cr X B B^{-1} & = A^{-1} B A^{-1} B^{-1} \cr X & = A^{-1} B A^{-1} B^{-1} \cr}$

Notice that I can multiply both sides of a matrix equation by the same thing, but I must multiply on the same side of both sides. So when I multiplied by $A^{-2}$ , I had to put $A^{-2}$ on the left side of both sides of the equation.

Once again, the reason I have to be careful is that in general, $M N \ne N M$ --- matrix multiplication is not commutative.

Example. Give a specific example of two invertible $2 \times 2$ real matrices A and B for which

$(A + B)^{-1} \ne A^{-1} + B^{-1}.$

One way to get a counterexample is to choose A and B so that isn't invertible. For instance,

$A = \left[\matrix{ 1 & 0 \cr 0 & 1 \cr}\right] \quad\hbox{and}\quad B = \left[\matrix{ -1 & 0 \cr 0 & -1 \cr}\right].$

Then A and B happen to be equal to their inverses:

$A^{-1} = \left[\matrix{ 1 & 0 \cr 0 & 1 \cr}\right] \quad\hbox{and}\quad B^{-1} = \left[\matrix{ -1 & 0 \cr 0 & -1 \cr}\right].$

But

$A + B = \left[\matrix{0 & 0 \cr 0 & 0 \cr}\right].$

The zero matrix is not invertible, because $0 \cdot C = 0$ for any matrix C --- so for no matrix C can $0 \cdot C = I$ .

But this feels like "cheating", because the left side $(A + B)^{-1}$ of the equation isn't defined. Okay --- can we find two matrices A and B for which $(A + B)^{-1} \ne A^{-1} + B^{-1}$ and both sides of the equation are defined? Thus, we need A, B, and to all be invertible.

I'll use

$A = \left[\matrix{ 1 & 0 \cr 1 & 1 \cr}\right] \quad\hbox{and}\quad B = \left[\matrix{ 0 & 1 \cr 1 & 0 \cr}\right].$

Then

$A^{-1} = \left[\matrix{ 1 & 0 \cr -1 & 1 \cr}\right] \quad\hbox{and}\quad B^{-1} = \left[\matrix{ 0 & 1 \cr 1 & 0 \cr}\right].$

(You can find the inverses using the formula for the inverse of a $2 \times 2$ matrix which I gave when I discussed matrix arithmetic. You can also find the inverses using row reduction.)

Thus,

$A^{-1} + B^{-1} = \left[\matrix{ 1 & 1 \cr 0 & 1 \cr}\right].$

On the other hand,

$A + B = \left[\matrix{ 1 & 1 \cr 2 & 1 \cr}\right] \quad\hbox{so}\quad (A + B)^{-1} = \left[\matrix{ -1 & 1 \cr 2 & -1 \cr}\right].$

Thus, $(A + B)^{-1} \ne A^{-1} + B^{-1}$ even though both sides of the equation are defined.

The next result connects several of the ideas we've looked at: Row reduction, elementary matrices, invertibility, and solving systems of equations.

Theorem. Let A be an $n \times n$ matrix. The following are equivalent:

(a) A is row equivalent to I.

(b) A is a product of elementary matrices.

(d) The only solution to the following system is the vector :

(e) For any n-dimensional vector b, the following system has a unique solution:

Proof. When you are trying to prove several statements are equivalent, you must prove that if you assume any one of the statements, you can prove any of the others. I can do this here by proving that (a) implies (b), (b) implies (c), (c) implies (d), (d) implies (e), and (e) implies (a).

(a) $\Rightarrow$ (b): Let $E_1, \ldots, E_p$ be elementary matrices which row reduce A to I:

$E_1 \cdots E_p A = I.$

Then

$A = E_p^{-1} \cdots E_1^{-1}.$

Since the inverse of an elementary matrix is an elementary matrix, A is a product of elementary matrices.

(b) $\Rightarrow$ (c): Write A as a product of elementary matrices:

$A = F_1 \cdots F_q.$

Now

$F_1 \cdots F_q \cdot F_q^{-1} \cdots F_1^{-1} = I,$

$F_q^{-1} \cdots F_1^{-1} \cdot F_1 \cdots F_q = I.$

Hence,

$A^{-1} = F_q^{-1} \cdots F_1^{-1}.$

Moreover, if y is any other solution, then

$Ay = 0, \quad\hbox{so}\quad A^{-1}Ay = A^{-1}0, \quad\hbox{or}\quad y = 0.$

That is, 0 is the one and only solution to the system.

(d) $\Rightarrow$ (e): Suppose the only solution to is . If $A = (a_{ij})$ , this means that row reducing the augmented matrix

$\left[\matrix{a_{11} & a_{12} & \cdots & a_{1n} & 0 \cr a_{21} & a_{22} & \cdots & a_{2n} & 0 \cr \vdots & \vdots & \ddots & \vdots \cr a_{n1} & a_{n2} & \cdots & a_{nn} & 0 \cr}\right] \quad\hbox{produces}\quad \left[\matrix{1 & 0 & \cdots & 0 & 0 \cr 0 & 1 & \cdots & 0 & 0 \cr \vdots & \vdots & \ddots & \vdots & \vdots \cr 0 & 0 & \cdots & 1 & 0 \cr}\right].$

Ignoring the last column (which never changes), this means there is a sequence of row operations , ..., which reduces A to the identity I --- that is, A is row equivalent to I. (I've actually proved (d) $\Rightarrow$ (a) at this point.)

Let $b = \langle b_1, \ldots b_n\rangle$ be an arbitrary n-dimensional vector. Then

$E_1\cdots E_n \left[\matrix{a_{11} & a_{12} & \cdots & a_{1n} & b_1 \cr a_{21} & a_{22} & \cdots & a_{2n} & b_2 \cr \vdots & \vdots & \ddots & \vdots \cr a_{n1} & a_{n2} & \cdots & a_{nn} & b_n \cr}\right] = \left[\matrix{1 & 0 & \cdots & 0 & b_1' \cr 0 & 1 & \cdots & 0 & b_2' \cr \vdots & \vdots & \ddots & \vdots & \vdots \cr 0 & 0 & \cdots & 1 & b_n' \cr}\right].$

Thus, $z = \langle b_1', \ldots b_n'\rangle$ is a solution.

Suppose y is another solution to . Then

Therefore, is a solution to . But the only solution to is 0, so , or . Thus, $z = \langle b_1', \ldots b_n'\rangle$ is the unique solution to .

(e) $\Rightarrow$ (a): Suppose has a unique solution for every b. As a special case, has a unique solution (namely ). But arguing as I did in (d) $\Rightarrow$ (e), I can show that A row reduces to I, and that is (a).

Remark. We'll see that there are many other conditions that are equivalent to a matrix being invertible. For instance, when we study determinants, we'll find that a matrix is invertible if and only if its determinant is invertible as a number.

If A is invertible, the theorem implies that A can be written as a product of elementary matrices. To do this, row reduce A to the identity, keeping track of the row operations you're using. Write each row operation as an elementary matrix, and express the row reduction as a matrix multiplication. Finally, solve the resulting equation for A.

Example. ( Writing an invertible matrix as a product of elementary matrices) Express the following real matrix as a product of elementary matrices:

$A = \left[\matrix{2 & -4 \cr -2 & 3 \cr}\right].$

First, row reduce A to I:

$\left[\matrix{2 & -4 \cr -2 & 3 \cr}\right] \matrix{\rightarrow \cr r_1 \to r_1/2 \cr} \left[\matrix{1 & -2 \cr -2 & 3 \cr}\right] \matrix{\rightarrow \cr r_2 \to r_2 + 2r_1 \cr}$

$\left[\matrix{1 & -2 \cr 0 & 1 \cr}\right] \matrix{\rightarrow \cr r_1 \to r_1 + 2r_2 \cr} \left[\matrix{1 & 0 \cr 0 & 1 \cr}\right]$

Next, represent each row operation as an elementary matrix:

$r_1 \to \dfrac{1}{2}r_1 \quad\hbox{corresponds to}\quad \left[\matrix{\dfrac{1}{2} & 0 \cr \noalign{\vskip2pt} 0 & 1 \cr}\right],$

$r_2 \to r_2 + 2r_1 \quad\hbox{corresponds to}\quad \left[\matrix{1 & 0 \cr 2 & 1 \cr}\right],$

$r_1 \to r_1 + 2r_2 \quad\hbox{corresponds to}\quad \left[\matrix{1 & 2 \cr 0 & 1 \cr}\right].$

Using the elementary matrices, write the row reduction as a matrix multiplication. A must be multiplied on the left by the elementary matrices in the order in which the operations were performed.

$\left[\matrix{1 & 2 \cr 0 & 1 \cr}\right] \left[\matrix{1 & 0 \cr 2 & 1 \cr}\right] \left[\matrix{\dfrac{1}{2} & 0 \cr \noalign{\vskip2pt} 0 & 1 \cr}\right]\cdot A = I.$

Solve the last equation for A, being careful to get the inverses in the right order:

$\left[\matrix{ \dfrac{1}{2} & 0 \cr \noalign{\vskip2pt} 0 & 1 \cr}\right]^{-1} \left[\matrix{1 & 0 \cr 2 & 1 \cr}\right]^{-1} \left[\matrix{1 & 2 \cr 0 & 1 \cr}\right]^{-1} \left[\matrix{1 & 2 \cr 0 & 1 \cr}\right] \left[\matrix{1 & 0 \cr 2 & 1 \cr}\right] \left[\matrix{\dfrac{1}{2} & 0 \cr \noalign{\vskip2pt} 0 & 1 \cr}\right]\cdot A = \left[\matrix{\dfrac{1}{2} & 0 \cr \noalign{\vskip2pt} 0 & 1 \cr}\right]^{-1} \left[\matrix{1 & 0 \cr 2 & 1 \cr}\right]^{-1} \left[\matrix{1 & 2 \cr 0 & 1 \cr}\right]^{-1}\cdot I,$

$A = \left[\matrix{ \dfrac{1}{2} & 0 \cr \noalign{\vskip2pt} 0 & 1 \cr}\right]^{-1} \left[\matrix{1 & 0 \cr 2 & 1 \cr}\right]^{-1} \left[\matrix{1 & 2 \cr 0 & 1 \cr}\right]^{-1}.$

Finally, write each inverse as an elementary matrix.

$A = \left[\matrix{2 & 0 \cr 0 & 1 \cr}\right] \left[\matrix{1 & 0 \cr -2 & 1 \cr}\right] \left[\matrix{1 & -2 \cr 0 & 1 \cr}\right].$

You can check your answer by multiplying the matrices on the right.

For two $n \times n$ matrices A and B to be inverses, I must have

$A B = I \quad\hbox{and}\quad B A = I.$

Since in general need not equal , it seems as though I must check that both equations hold in order to show that A and B are inverses. It turns out that, thanks to the earlier theorem, we only need to check that .

Corollary. If A and B are $n \times n$ matrices and , then $A = B^{-1}$ and .

Proof. Suppose A and B are $n \times n$ matrices and . The system certainly has as a solution. I'll show it's the only solution.

Suppose y is another solution, so

Multiply both sides by A and simplify:

$\eqalign{ A B y & = A \cdot 0 \cr I y & = 0 \cr y & = 0 \cr}$

Thus, 0 is a solution, and it's the only solution.

Thus, B satisfies condition (d) of the Theorem. Since the five conditions are equivalent, B also satisfies condition (c), so B is invertible. Let $B^{-1}$ be the inverse of B. Then

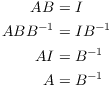
$\eqalign{ A B & = I \cr A B B^{-1} & = I B^{-1} \cr A I & = B^{-1} \cr A & = B^{-1} \cr}$

This proves the first part of the Corollary. Finally,

$B A = B B^{-1} = I.$

This finishes the proof.

The proof of the theorem gives an algorithm for inverting a matrix A.

If A is invertible, there are elementary matrices $E_1, \ldots, E_p$ which row reduce A to I:

$E_1 \cdots E_p A = I.$

But this equation says that $E_1 \cdots E_p$ is the inverse of A, since multiplying A by $E_1 \cdots E_p$ gives the identity. Thus,

$A^{-1} = E_1 \cdots E_p = E_1 \cdots E_p \cdot I.$

We can interpret the last expression $E_1 \cdots E_p \cdot I$ as applying the row operations for , ... to the identity matrix I. And the same row operations row reduce A to I. So form an augmented matrix by placing the identity matrix next to A:

$\hbox{\epsfysize=1in \epsffile{inverses-and-elementary-matrices-2.eps}}$

Row reduce the augmented matrix. The left-hand block A will row reduce to the identity; at the same time, the right-hand block I will be transformed into $A^{-1}$ .

Example. Invert the following matrix over $\real$ :

$\left[\matrix{ 1 & 2 & -1 \cr -1 & -1 & 3 \cr 0 & 1 & 1 \cr}\right].$

Form the augmented matrix by putting the $3 \times 3$ identity matrix on the right of the original matrix:

$\left[\matrix{ 1 & 2 & -1 \cr -1 & -1 & 3 \cr 0 & 1 & 1 \cr}\right| \left.\matrix{ 1 & 0 & 0 \cr 0 & 1 & 0 \cr 0 & 0 & 1 \cr}\right].$

Next, row reduce the augmented matrix. The row operations are entirely determined by the block on the left, which is the original matrix. The row operations turn the left block into the identity, while simultaneously turning the identity in the right block into the inverse.

$\left[\matrix{ 1 & 2 & -1 \cr -1 & -1 & 3 \cr 0 & 1 & 1 \cr}\right| \left.\matrix{ 1 & 0 & 0 \cr 0 & 1 & 0 \cr 0 & 0 & 1 \cr}\right] \quad\matrix{\rightarrow \cr r_2 \to r_2 + r_1 \cr}\quad \left[\matrix{ 1 & 2 & -1 \cr 0 & 1 & 2 \cr 0 & 1 & 1 \cr}\right| \left.\matrix{ 1 & 0 & 0 \cr 1 & 1 & 0 \cr 0 & 0 & 1 \cr}\right] \quad\matrix{\rightarrow \cr r_3 \to r_3 - r_2 \cr}$

$\left[\matrix{ 1 & 2 & -1 \cr 0 & 1 & 2 \cr 0 & 0 & -1 \cr}\right| \left.\matrix{ 1 & 0 & 0 \cr 1 & 1 & 0 \cr -1 & -1 & 1 \cr}\right] \quad\matrix{\rightarrow \cr r_1 \to r_1 - 2 r_2 \cr}\quad \left[\matrix{ 1 & 0 & -5 \cr 0 & 1 & 2 \cr 0 & 0 & -1 \cr}\right| \left.\matrix{ -1 & -2 & 0 \cr 1 & 1 & 0 \cr -1 & -1 & 1 \cr}\right] \quad\matrix{\rightarrow \cr r_3 \to -r_3 \cr}$

$\left[\matrix{ 1 & 0 & -5 \cr 0 & 1 & 2 \cr 0 & 0 & 1 \cr}\right| \left.\matrix{ -1 & -2 & 0 \cr 1 & 1 & 0 \cr 1 & 1 & -1 \cr}\right] \quad\matrix{\rightarrow \cr r_1 \to r_1 + 5 r_3 \cr}\quad \left[\matrix{ 1 & 0 & 0 \cr 0 & 1 & 2 \cr 0 & 0 & 1 \cr}\right| \left.\matrix{ 4 & 3 & -5 \cr 1 & 1 & 0 \cr 1 & 1 & -1 \cr}\right] \quad\matrix{\rightarrow \cr r_2 \to r_2 - 2 r_3 \cr}$

$\left[\matrix{ 1 & 0 & 0 \cr 0 & 1 & 0 \cr 0 & 0 & 1 \cr}\right| \left.\matrix{ 4 & 3 & -5 \cr -1 & -1 & 2 \cr 1 & 1 & -1 \cr}\right].$

Thus,

$\left[\matrix{ 1 & 2 & -1 \cr -1 & -1 & 3 \cr 0 & 1 & 1 \cr}\right]^{-1} = \left[\matrix{ 4 & 3 & -5 \cr -1 & -1 & 2 \cr 1 & 1 & -1 \cr}\right].\quad\halmos$

In the future, I won't draw the vertical bar between the two blocks; you can draw it if it helps you keep the computation organized.

Example. ( Inverting a matrix over $\integer_p$ ) Find the inverse of the following matrix over $\integer_3$ :

$\left[\matrix{ 1 & 0 & 2 \cr 1 & 1 & 1 \cr 2 & 1 & 1 \cr}\right].$

Form the augmented matrix and row reduce:

$\left[\matrix{ 1 & 0 & 2 & 1 & 0 & 0 \cr 1 & 1 & 1 & 0 & 1 & 0 \cr 2 & 1 & 1 & 0 & 0 & 1 \cr}\right] \matrix{\rightarrow \cr r_2 \to r_2 - r_1 \cr} \left[\matrix{ 1 & 0 & 2 & 1 & 0 & 0 \cr 0 & 1 & 2 & 2 & 1 & 0 \cr 2 & 1 & 1 & 0 & 0 & 1 \cr}\right] \matrix{\rightarrow \cr r_3 \to r_3 - 2 r_1 \cr}$

$\left[\matrix{ 1 & 0 & 2 & 1 & 0 & 0 \cr 0 & 1 & 2 & 2 & 1 & 0 \cr 0 & 1 & 0 & 1 & 0 & 1 \cr}\right] \matrix{\rightarrow \cr r_3 \to r_3 - r_2 \cr} \left[\matrix{ 1 & 0 & 2 & 1 & 0 & 0 \cr 0 & 1 & 2 & 2 & 1 & 0 \cr 0 & 0 & 1 & 2 & 2 & 1 \cr}\right] \matrix{\rightarrow \cr r_1 \to r_1 - 2 r_3 \cr}$

$\left[\matrix{ 1 & 0 & 0 & 0 & 2 & 1 \cr 0 & 1 & 2 & 2 & 1 & 0 \cr 0 & 0 & 1 & 2 & 2 & 1 \cr}\right] \matrix{\rightarrow \cr r_2 \to r_2 - 2 r_3 \cr} \left[\matrix{ 1 & 0 & 0 & 0 & 2 & 1 \cr 0 & 1 & 0 & 1 & 0 & 1 \cr 0 & 0 & 1 & 2 & 2 & 1 \cr}\right]$

Therefore,

$\left[\matrix{ 1 & 0 & 2 \cr 1 & 1 & 1 \cr 2 & 1 & 1 \cr}\right]^{-1} = \left[\matrix{ 0 & 2 & 1 \cr 1 & 0 & 1 \cr 2 & 2 & 1 \cr}\right].\quad\halmos$

The theorem also tells us about the number of solutions to a system of linear equations.

Proposition. Let F be a field, and let be a system of linear equations over F. Then:

(a) If F is infinite, then the system has either no solutions, exactly one solution, or infinitely many solutions.

(b) If F is a finite field with elements, where p is prime and $n \ge 1$ , then the system has either no solutions, exactly one solution, or at least solutions.

Proof. Suppose the system has more than one solution. I must show that there are infinitely many solutions if F is infinite, or at least solutions if F is a finite field with elements.

Since there is more than one solution, there are at least two different solutions. So let and be two different solutions to :

$A x_1 = b \quad\hbox{and}\quad A x_2 = b.$

Subtracting the equations gives

Since $x_1 - x_2 \ne 0$ , is a nontrivial solution to the system . Now if $t \in F$ ,

$A\left(x_1 + t(x_1 - x_2)\right) = A x_1 + t \cdot A(x_1 - x_2) = b + 0 = b.$

Thus, is a solution to . Moreover, the only way two solutions of the form can be the same is if they have the same t. For

$x_1 + t(x_1 - x_2) = x_1 + t'(x_1 - x_2) \quad\hbox{gives}\quad t(x_1 - x_2) = t'(x_1 - x_2).$

Since $x_1 \ne x_2$ , I have $x_1 - x_2 \ne 0$ . So I can divide both sides by , and I get .

Thus, different t's give different 's, each of which is a solution to the system.

If F has infinitely many elements, there are infinitely many possibilities for t, so there are infinitely many solutions.

If F has elements, there are possibilities for t, so there are at least solutions. (Note that there may be solutions which are not of the form , so there may be more than solutions. In fact, I'll be able to show later than the number of solutions will be some power of .)

For example, since $\real$ is an infinite field, a system of linear equations over $\real$ has no solutions, exactly one solution, or infinitely many solutions.

On the other hand, since $\integer_3$ is a field with 3 elements, a system of linear equations over $\integer_3$ has no solutions, exactly one solution, or at least 3 solutions. (And I'll see later that if there's more than one solution, then there might be 3 solutions, 9 solutions, 27 solutions, ....)

Contact information

Bruce Ikenaga's Home Page