Linear Independence

Definition. Let V be a vector space over a field F, and let $S \subset V$ . The set S is linearly independent if $v_1, \ldots, v_n \in S$ , $a_1, \ldots, a_n \in F$ , and

$$a_1 v_1 + \cdots + a_n v_n = 0 \quad \hbox{implies} \quad a_1 = \cdots = a_n = 0.$$

A set of vectors which is not linearly independent is linearly dependent. (I'll usually say "independent" and "dependent" for short.) Thus, a set of vectors S is dependent if there are vectors $v_1, \ldots, v_n \in S$ and numbers $a_1, \ldots, a_n \in F$ , not all of which are 0, such that

$$a_1 v_1 + \cdots + a_n v_n = 0.$$

Note that S could be an infinite set of vectors.

In words, the definition says that if a linear combination of any finite set of vectors in S equals the zero vector, then all the coefficients in the linear combination must be 0. I'll refer to such a linear combination as a trivial linear combination.

On the other hand, a linear combination of vectors is nontrivial if at least one of the coefficients is nonzero. ("At least one" doesn't mean "all" --- a nontrivial linear combination can have some zero coefficients, as long as at least one is nonzero.)

Thus, we can also say that a set of vectors is independent if there is no nontrivial linear combination among finitely many of the vectors which is equal to 0. And a set of vectors is dependent if there is some nontrivial linear combination among finitely many of the vectors which is equal to 0.

Let's see a pictorial example of a dependent set. Consider the following vectors u, v, and w in $\real^2$ .

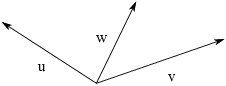
$$\hbox{\epsfysize=0.75in \epsffile{linear-independence-1.eps}}$$

I'll show how to get a nontrivial linear combination of the vectors that is equal to the zero vector. Project w onto the lines of u and v.

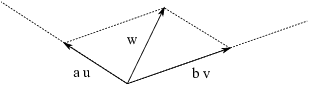
$$\hbox{\epsfysize=0.75in \epsffile{linear-independence-2.eps}}$$

The projections are multiples $a u$ of u and $b v$ of v. Since w is the diagonal of the parallelogram whose sides are $a u$ and $b v$ , we have

$$w = a u + b v, \quad\hbox{so}\quad a u + b v - w = 0.$$

This is a nontrivial linear combination of u, v and w which is equal to the zero vector, so $\{u, v, w\}$ is dependent.

In fact, it's true that any 3 vectors in $\real^2$ are dependent, and this pictorial example should make this reasonable. More generally, if F is a field then any n vectors in $F^m$ are dependent if $n > m$ . We'll prove this below.

Example. If F is a field, the standard basis vectors are

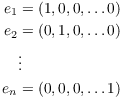
$$\eqalign{ e_1 & = (1, 0, 0 , \ldots 0) \cr e_2 & = (0, 1, 0, \ldots 0) \cr & \vdots \cr e_n & = (0, 0, 0, \ldots 1) \cr}$$

Show that they form an independent set in $F^n$ .

Write

$$a_1 e_1 + a_2 e_2 + \cdots + a_n e_n = 0.$$

I have to show all the a's are 0. Now

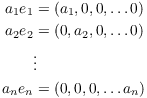
$$\eqalign{ a_1 e_1 & = (a_1, 0, 0 , \ldots 0) \cr a_2 e_2 & = (0, a_2, 0, \ldots 0) \cr & \vdots \cr a_n e_n & = (0, 0, 0, \ldots a_n) \cr}$$

So

$$a_1 e_1 + a_2 e_2 + \cdots + a_n e_n = (a_1, a_2, \ldots a_n).$$

Since by assumption $a_1 e_1 + a_2 e_2 + \cdots + a_n e_n = 0$ , I get

$$(a_1, a_2, \ldots a_n) = (0, 0, \ldots 0).$$

Hence, $a_1 = a_2 = \cdots = a_n = 0$ , and the set is independent.

Example. Show that any set containing the zero vector is dependent.

If $0 \in S$ , then $1 \cdot 0 = 0$ . The left side is a nontrivial (since $1 \ne 0$ ) linear combination of vectors in S --- actually, a vector in S. The linear combination is equal to 0. Hence, S is dependent.

Notice that it doesn't matter what else is in S (if anything).

Example. Show that the vectors $(2, -1, 4)$ and $(-6, 3, -12)$ are dependent in $\real^3$ .

I have to find numbers a and b, not both 0, such that

$$a \cdot (2, -1, 4) + b \cdot (-6, 3, -12) = (0, 0, 0).$$

In this case, you can probably juggle numbers in your head to see that

$$3 \cdot (2, -1, 4) + 1 \cdot (-6, 3, -12) = (0, 0, 0).$$

This shows that the vectors are dependent. There are infinitely many pairs of numbers a and b that work. In examples to follow, I'll show how to find numbers systematically in cases where the arithmetic isn't so easy.

Example. Suppose u, v, w, and x are vectors in a vector space. Prove that the set $\{u - v, v - w, w - x, x - u\}$ is dependent.

Notice that in the four vectors in $\{u - v, v - w, w - x, x - u\}$ , each of u, v, w, and x occurs once with a plus sign and once with a minus sign. So

$$(u - v) + (v - w) + (w - x) + (x - u) = 0.$$

This is a dependence relation, so the set is dependent.

If you can't see an "easy" linear combination of a set of vectors that equals 0, you may have to determine independence or dependence by solving a system of equations.

Example. Consider the following sets of vectors in $\real^3$ . If the set is independent, prove it. If the set is dependent, find a nontrivial linear combination of the vectors which is equal to 0.

(a) $\{(2, 0, -3), (1, 1, 1), (1, 7, 2)\}$ .

(b) $\{(1, 2, -1), (4, 1, 3), (-10, 1, -11)\}$ .

(a) Write a linear combination of the vectors and set it equal to 0:

$$a \cdot \left[\matrix{2 \cr 0 \cr -3 \cr}\right] + b \cdot \left[\matrix{1 \cr 1 \cr 1 \cr}\right] + c \cdot \left[\matrix{1 \cr 7 \cr 2 \cr}\right] = \left[\matrix{0 \cr 0 \cr 0 \cr}\right].$$

I have to determine whether this implies that $a = b = c = 0$ .

Note: When I convert vectors given in "parenthesis form" to "matrix form", I'll turn the vectors into column vectors as above. This is consistent with the way I've set up systems of linear equations. Thus,

$$(2, 0, -3) \quad\hbox{became}\quad \left[\matrix{2 \cr 0 \cr -3 \cr}\right].$$

The vector equation above is equivalent to the matrix equation

$$\left[\matrix{ 2 & 1 & 1 \cr 0 & 1 & 7 \cr -3 & 1 & 2 \cr}\right] \left[\matrix{a \cr b \cr c \cr}\right] = \left[\matrix{0 \cr 0 \cr 0 \cr}\right].$$

Row reduce to solve:

$$\left[\matrix{ 2 & 1 & 1 & 0 \cr 0 & 1 & 7 & 0 \cr -3 & 1 & 2 & 0 \cr}\right] \quad \to \quad \left[\matrix{ 1 & 0 & 0 & 0 \cr 0 & 1 & 0 & 0 \cr 0 & 0 & 1 & 0 \cr}\right]$$

Note: Row operations won't change the last column of zeros, so you don't actually need to write it when you do the row reduction. I'll put it in to avoid confusion.

The last matrix gives the equations

$$a = 0, \quad b = 0, \quad c = 0.$$

Therefore, the vectors are independent.

(b) Write

$$a \cdot \left[\matrix{1 \cr 2 \cr -1 \cr}\right] + b \cdot \left[\matrix{4 \cr 1 \cr 3 \cr}\right] + c \cdot \left[\matrix{-10 \cr 1 \cr -11 \cr}\right] = \left[\matrix{0 \cr 0 \cr 0 \cr}\right].$$

This gives the matrix equation

$$\left[\matrix{ 1 & 4 & -10 \cr 2 & 1 & 1 \cr -1 & 3 & -11 \cr}\right] \left[\matrix{a \cr b \cr c \cr}\right] = \left[\matrix{0 \cr 0 \cr 0 \cr}\right].$$

Row reduce to solve:

$$\left[\matrix{ 1 & 4 & -10 & 0 \cr 2 & 1 & 1 & 0 \cr -1 & 3 & -11 & 0 \cr}\right] \quad \to \quad \left[\matrix{ 1 & 0 & 2 & 0 \cr 0 & 1 & -3 & 0 \cr 0 & 0 & 0 & 0 \cr}\right]$$

This gives the equations

$$a + 2 c = 0, \quad b - 3 c = 0.$$

Thus, $a = - 2 c$ and $b = 3 c$ . I can get a nontrivial solution by setting c to any nonzero number. I'll use $c = 1$ . This gives $a = -2$ and $b = 3$ . So

$$(-2) \cdot \left[\matrix{1 \cr 2 \cr -1 \cr}\right] + 3 \cdot \left[\matrix{4 \cr 1 \cr 3 \cr}\right] + 1 \cdot \left[\matrix{-10 \cr 1 \cr -11 \cr}\right] = \left[\matrix{0 \cr 0 \cr 0 \cr}\right].$$

This is a linear dependence relation, and the vectors are dependent.

The same approach works for vectors in $F^n$ where F is a field other than the real numbers.

Example. Consider the set of vectors

$$\left\{(4, 1, 2), (3, 3, 0), (0, 1, 1)\right\} \quad\hbox{in}\quad \integer_5^3.$$

If the set is independent, prove it. If the set is dependent, find a nontrivial linear combination of the vectors which is equal to 0.

Write

$$a \cdot \left[\matrix{4 \cr 1 \cr 2 \cr}\right] + b \cdot \left[\matrix{3 \cr 3 \cr 0 \cr}\right] + c \cdot \left[\matrix{0 \cr 1 \cr 1 \cr}\right] = \left[\matrix{0 \cr 0 \cr 0 \cr}\right].$$

This gives the matrix equation

$$\left[\matrix{ 4 & 3 & 0 \cr 1 & 3 & 1 \cr 2 & 0 & 1 \cr}\right] \left[\matrix{a \cr b \cr c \cr}\right] = \left[\matrix{0 \cr 0 \cr 0 \cr}\right].$$

Row reduce to solve the system:

$$\left[\matrix{ 4 & 3 & 0 & 0 \cr 1 & 3 & 1 & 0 \cr 2 & 0 & 1 & 0 \cr}\right] \matrix{\to \cr r_{1} \to 4 r_{1} \cr} \left[\matrix{ 1 & 2 & 0 & 0 \cr 1 & 3 & 1 & 0 \cr 2 & 0 & 1 & 0 \cr}\right] \matrix{\to \cr r_{3} \to r_{3} + 3 r_{1} \cr}$$

$$\left[\matrix{ 1 & 2 & 0 & 0 \cr 1 & 3 & 1 & 0 \cr 0 & 1 & 1 & 0 \cr}\right] \matrix{\to \cr r_{2} \to r_{2} + 4 r_{1} \cr} \left[\matrix{ 1 & 2 & 0 & 0 \cr 0 & 1 & 1 & 0 \cr 0 & 1 & 1 & 0 \cr}\right] \matrix{\to \cr r_{1} \to r_{1} + 3 r_{2} \cr}$$

$$\left[\matrix{ 1 & 0 & 3 & 0 \cr 0 & 1 & 1 & 0 \cr 0 & 1 & 1 & 0 \cr}\right] \matrix{\to \cr r_{3} \to r_{3} + 4 r_{2} \cr} \left[\matrix{ 1 & 0 & 3 & 0 \cr 0 & 1 & 1 & 0 \cr 0 & 0 & 0 & 0 \cr}\right]$$

This gives the equations

$$a + 3 c = 0, \quad b + c = 0.$$

Thus, $a = 2 c$ and $b = 4 c$ . Set $c = 1$ . This gives $a = 2$ and $b = 4$ . Hence, the set is dependent, and

$$2 \cdot \left[\matrix{4 \cr 1 \cr 2 \cr}\right] + 4 \cdot \left[\matrix{3 \cr 3 \cr 0 \cr}\right] + 1 \cdot \left[\matrix{0 \cr 1 \cr 1 \cr}\right] = \left[\matrix{0 \cr 0 \cr 0 \cr}\right].\quad\halmos$$

Example. Consider the following set of vectors in $\integer_3^4$ :

$$\left\{(1, 0, 1, 2), (1, 2, 2, 1), (0, 1, 2, 1)\right\}$$

If the set is independent, prove it. If the set is dependent, find a nontrivial inear combination of the vectors equal to 0.

Write

$$a \cdot \left[\matrix{1 \cr 0 \cr 1 \cr 2 \cr}\right] + b \cdot \left[\matrix{1 \cr 2 \cr 2 \cr 1 \cr}\right] + c \cdot \left[\matrix{0 \cr 1 \cr 2 \cr 1 \cr}\right] = \left[\matrix{0 \cr 0 \cr 0 \cr 0 \cr}\right].$$

This gives the matrix equation

$$\left[\matrix{ 1 & 1 & 0 \cr 0 & 2 & 1 \cr 1 & 2 & 2 \cr 2 & 1 & 1 \cr}\right] \left[\matrix{a \cr b \cr c \cr}\right] = \left[\matrix{0 \cr 0 \cr 0 \cr 0 \cr}\right].$$

Row reduce to solve the system:

$$\left[\matrix{ 1 & 1 & 0 & 0 \cr 0 & 2 & 1 & 0 \cr 1 & 2 & 2 & 0 \cr 2 & 1 & 1 & 0 \cr}\right] \quad \to \quad \left[\matrix{ 1 & 0 & 1 & 0 \cr 0 & 1 & 2 & 0 \cr 0 & 0 & 0 & 0 \cr 0 & 0 & 0 & 0 \cr}\right]$$

This gives the equations

$$a + c = 0, \quad b + 2 c = 0.$$

Hence, $a = 2 c$ and $b = c$ . Set $c = 1$ . Then $a = 2$ and $b = 1$ . Therefore, the set is dependent, and

$$2 \cdot \left[\matrix{1 \cr 0 \cr 1 \cr 2 \cr}\right] + 1 \cdot \left[\matrix{1 \cr 2 \cr 2 \cr 1 \cr}\right] + 1 \cdot \left[\matrix{0 \cr 1 \cr 2 \cr 1 \cr}\right] = \left[\matrix{0 \cr 0 \cr 0 \cr 0 \cr}\right].\quad\halmos$$

To summarize, to determine whether vectors $v_1$ , $v_2$ , ..., $v_m$ in a vector space V are independent, I try to solve

$$a_1 v_1 + a_2 v_2 + \cdots + a_m v_m = 0.$$

If the only solution is $a_1 = a_2 = \cdots = a_m = 0$ , then the vectors are independent; otherwise, they are dependent.

It's important to understand this general setup, and not just memorize the special case of vectors in $F^n$ , as shown in the last few examples. Remember that vectors don't have to look like things like "$(-3, 5, 7, 0)$ " ("numbers in slots"). Consider the next example, for instance.

Example. $\real[x]$ is a vector space over the reals. Show that the set $\{1, x, x^2, \ldots \}$ is independent.

Suppose

$$a_0 + a_1 x + a_2 x^2 + \cdots + a_n x^n = 0.$$

That is,

$$a_0 + a_1 x + a_2 x^2 + \cdots + a_n x^n = 0 + 0 \cdot x + 0 \cdot x^2 + \cdots + 0 \cdot x^n.$$

Two polynomials are equal if and only if their corresponding coefficients are equal. Hence, $a_0 = a_2 = \cdots = a_n = 0$ . Therefore, $\{1, x, x^2, \ldots \}$ is independent.

In some cases, you can tell by inspection that a set is dependent. I noted earlier that a set containing the zero vector must be dependent. Here's another easy case.

Proposition. If $n > m$ , a set of n vectors in $F^m$ is dependent.

Proof. Suppose $v_1, v_2, \ldots v_n$ are n vectors in $F^m$ , and $n > m$ . Write

$$a_1 v_1 + a_2 v_2 + \cdots + a_n v_n = 0.$$

This gives the matrix equation

$$\left[\matrix{ \uparrow & \uparrow & & \uparrow \cr v_1 & v_2 & & v_n \cr \downarrow & \downarrow & & \downarrow \cr}\right] \left[\matrix{a_1 \cr a_2 \cr \vdots \cr a_n \cr}\right] = \left[\matrix{0 \cr 0 \cr \vdots \cr 0 \cr}\right].$$

To solve, I'd row reduce the matrix

$$\left[\matrix{ \uparrow & \uparrow & & \uparrow & 0 \cr v_1 & v_2 & & v_n & \vdots \cr \downarrow & \downarrow & & \downarrow & 0 \cr}\right]$$

Note that this matrix has m rows and $n + 1$ columns, and $n > m$ .

The row-reduced echelon form can have at most one leading coefficient in each row, so there are at most m leading coefficients. These correspond to the main variables in the solution. Since there are n variables and $n > m$ , there must be some parameter variables. By setting any parameter variables equal to nonzero numbers, I get a nontrivial solution for $a_1$ , $a_2$ , ... $a_n$ . This implies that $\{v_1, v_2, \ldots v_n\}$ is dependent.

Example. Is the following set of vectors in $\real^2$ independent or dependent?

$$\left\{(1, -3), (5, -\pi), (\sqrt{42}, 7)\right\}$$

Any set of three (or more) vectors in $\real^2$ is dependent.

Notice that we know this by just counting the number of vectors. To answer the given question, we don't actually have to give a nontrivial linear combination of the vectors that's equal to 0.

Proposition. Let $\{v_1, v_2, \ldots v_n\}$ be vectors in $F^n$ , where F is a field. $\{v_1, v_2, \ldots v_n\}$ is independent if and only if the matrix constructed using the vectors as columns is invertible:

$$\left[\matrix{ \uparrow & \uparrow & & \uparrow \cr v_1 & v_2 & & v_n \cr \downarrow & \downarrow & & \downarrow \cr}\right].$$

Proof. Suppose the set is independent. Consider the system

$$\left[\matrix{ \uparrow & \uparrow & & \uparrow \cr v_1 & v_2 & & v_n \cr \downarrow & \downarrow & & \downarrow \cr}\right] \left[\matrix{a_1 \cr a_2 \cr \vdots \cr a_n \cr}\right] = \left[\matrix{0 \cr 0 \cr \vdots \cr 0 \cr}\right].$$

Multiplying out the left side, this gives

$$a_1 v_1 + a_2 v_2 + a_n v_n = 0.$$

By independence, $a_1 = a_2 = \cdots = a_n = 0$ . Thus, the system above has only the zero vector 0 as a solution. An earlier theorem on invertibility shows that this means the matrix of v's is invertible.

Conversely, suppose the following matrix is invertible:

$$A = \left[\matrix{ \uparrow & \uparrow & & \uparrow \cr v_1 & v_2 & & v_n \cr \downarrow & \downarrow & & \downarrow \cr}\right].$$

Let

$$a_1 v_1 + a_2 v_2 + a_n v_n = 0.$$

Write this as a matrix equation and solve it:

$$\eqalign{ \left[\matrix{ \uparrow & \uparrow & & \uparrow \cr v_1 & v_2 & & v_n \cr \downarrow & \downarrow & & \downarrow \cr}\right] \left[\matrix{a_1 \cr a_2 \cr \vdots \cr a_n \cr}\right] & = \left[\matrix{0 \cr 0 \cr \vdots \cr 0 \cr}\right] \cr A \cdot \left[\matrix{a_1 \cr a_2 \cr \vdots \cr a_n \cr}\right] & = \left[\matrix{0 \cr 0 \cr \vdots \cr 0 \cr}\right] \cr A^{-1} A \cdot \left[\matrix{a_1 \cr a_2 \cr \vdots \cr a_n \cr}\right] & = A^{-1} \cdot \left[\matrix{0 \cr 0 \cr \vdots \cr 0 \cr}\right] \cr \left[\matrix{a_1 \cr a_2 \cr \vdots \cr a_n \cr}\right] & = \left[\matrix{0 \cr 0 \cr \vdots \cr 0 \cr}\right] \cr}$$

This gives $a_1 = a_2 = \cdots = a_n = 0$ . Hence, the v's are independent.

Note that this proposition requires that you have n vectors in $F^n$ --- the number of vectors must match the dimension of the space.

The result can also be stated in contrapositive form: The set of vectors is dependent if and only if the matrix having the vectors as columns is not invertible. I'll use this form in the next example.

Example. Consider the following set of vectors in $\real^3$ :

$$\left\{ \left[\matrix{x - 8 \cr 0 \cr 0 \cr}\right], \left[\matrix{-7 \cr x - 1 \cr 0 \cr}\right], \left[\matrix{13 \cr 5 \cr 30 \cr}\right]\right\}.$$

For what values of x is the set dependent?

I have 3 vectors in $\real^3$ , so the previous result applies.

Construct the matrix having the vectors as columns:

$$A = \left[\matrix{ x - 8 & -7 & 13 \cr 0 & x - 1 & 5 \cr 0 & 0 & 30 \cr}\right].$$

The set is dependent when A is not invertible, and A is not invertible when its determinant is equal to 0. Now

$$\det A = 30(x - 1)(x - 8).$$

Thus, $\det A = 0$ for $x = 1$ and $x = 8$ . For those values of x, the original set is dependent.

The next proposition says that a independent set can be thought of as a set without "redundancy", in the sense that you can't build any one of the vectors out of the others.

Proposition. Let V be a vector space over a field F, and let $S \subset V$ . S is dependent if and only if some $v \in S$ can be expressed as a linear combination of vectors in S.

Proof. Suppose $v \in S$ can be written as a linear combination of vectors in S other than v:

$$v = a_1 v_1 + \cdots + a_n v_n.$$

Here $v_1, \ldots, v_n \in S$ (where $v_i \ne v$ for all i) and $a_1, \ldots, a_n \in F$ .

Then

$$0 = a_1 v_1 + \cdots + a_n v_n - 1 \cdot v.$$

This is a nontrivial linear relation among elements of S. Hence, S is dependent.

Conversely, suppose S is dependent. Then there are elements $a_1, a_2, \ldots a_n \in F$ (not all 0) and $v_1, v_2, \ldots v_n \in S$ such that

$$a_1 v_1 + a_2 v_2 + \cdots + a_n v_n = 0.$$

Since not all the a's are 0, at least one is nonzero. There's no harm in assuming that $a_1 \ne 0$ . (If another a was nonzero instead, just relabel the a's and v's so $a_1 \ne 0$ and start again.)

Since $a_1 \ne 0$ , its inverse $a_1^{-1}$ is defined. So

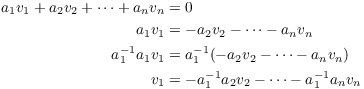
$$\eqalign{ a_1 v_1 + a_2 v_2 + \cdots + a_n v_n & = 0 \cr a_1 v_1 & = -a_2 v_2 - \cdots - a_n v_n \cr a_1^{-1} a_1 v_1 & = a_1^{-1} (-a_2 v_2 - \cdots - a_n v_n) \cr v_1 & = -a_1^{-1} a_2 v_2 - \cdots - a_1^{-1} a_n v_n \cr}$$

Thus, I've expressed $v_1$ as a linear combination of other vectors in S.

Independence of sets of functions

In some cases, we can use a determinant to tell that a finite set of functions is independent. The determinant is called the Wronskian, and its rows are the successive derivatives of the original functions.

Definition. Let $\{f_1, f_2, \ldots f_n\}$ be a set of functions $\real \to \real$ which are differentiable $n - 1$ times. The Wronskian is

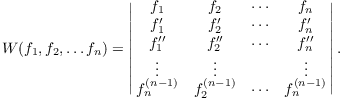
$$W(f_1, f_2, \ldots f_n) = \left|\matrix{ f_1 & f_2 & \cdots & f_n \cr f_1' & f_2' & \cdots & f_n' \cr f_1'' & f_2'' & \cdots & f_n'' \cr \vdots & \vdots & & \vdots \cr f_n^{(n - 1)} & f_2^{(n - 1)} & \cdots & f_n^{(n - 1)} \cr}\right|.$$

Naturally, this requires that the functions be sufficiently differentiable.

Theorem. Let $C^{n-1}(\real)$ be the real vector space of functions $\real \to \real$ which are differentiable $n - 1$ times. Let $S = \{f_1, f_2, \ldots f_n\}$ be a subset of $C^{n-1}(\real)$ .If $W(f_1, f_2, \ldots f_n) \ne 0$ at some point $x = c$ , then S is independent.

Thus, if you can find some value of x for which the Wronskian is nonzero, the functions are independent.

The converse is false, and we'll give a counterexample to the converse below. The converse does hold with additional conditions: For example, if the functions are solutions to a linear differential equation.

Proof. Let

$$a_1 f_1(x) + a_2 f_2(x) + \cdots + a_n f_n(x) = 0.$$

I have to show all the a's are 0.

This equation is an identity in x, so I may differentiate it repeatedly to get n equations:

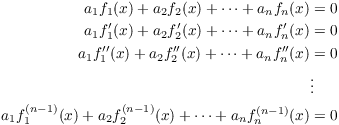
$$\eqalign{ a_1 f_1(x) + a_2 f_2(x) + \cdots + a_n f_n(x) & = 0 \cr a_1 f_1'(x) + a_2 f_2'(x) + \cdots + a_n f_n'(x) & = 0 \cr a_1 f_1''(x) + a_2 f_2''(x) + \cdots + a_n f_n''(x) & = 0 \cr & \vdots \cr a_1 f_1^{(n - 1)}(x) + a_2 f_2^{(n - 1)}(x) + \cdots + a_n f_n^{(n - 1)}(x) & = 0 \cr}$$

I can write this in matrix form:

$$\left[\matrix{ f_1(x) & f_2(x) & \cdots & f_n(x) \cr f_1'(x) & f_2'(x) & \cdots & f_n'(x) \cr f_1''(x) & f_2''(x) & \cdots & f_n''(x) \cr \vdots & \vdots & & \vdots \cr f_n^{(n - 1)}(x) & f_2^{(n - 1)}(x) & \cdots & f_n^{(n - 1)}(x) \cr}\right] \left[\matrix{a_1 \cr a_2 \cr \vdots \cr a_n \cr}\right] = \left[\matrix{0 \cr 0 \cr \vdots \cr 0 \cr}\right].$$

Plug in $x = c$ :

$$\left[\matrix{ f_1(c) & f_2(c) & \cdots & f_n(c) \cr f_1'(c) & f_2'(c) & \cdots & f_n'(c) \cr f_1''(c) & f_2''(c) & \cdots & f_n''(c) \cr \vdots & \vdots & & \vdots \cr f_n^{(n - 1)}(c) & f_2^{(n - 1)}(c) & \cdots & f_n^{(n - 1)}(c) \cr}\right] \left[\matrix{a_1 \cr a_2 \cr \vdots \cr a_n \cr}\right] = \left[\matrix{0 \cr 0 \cr \vdots \cr 0 \cr}\right].$$

Let

$$A = \left[\matrix{ f_1(c) & f_2(c) & \cdots & f_n(c) \cr f_1'(c) & f_2'(c) & \cdots & f_n'(c) \cr f_1''(c) & f_2''(c) & \cdots & f_n''(c) \cr \vdots & \vdots & & \vdots \cr f_n^{(n - 1)}(c) & f_2^{(n - 1)}(c) & \cdots & f_n^{(n - 1)}(c) \cr}\right].$$

The determinant of this matrix is the Wronskian $W(f_1, f_2, \ldots f_n)(c)$ , which by assumption is nonzero. Since the determinant is nonzero, the matrix is invertible. So

$$\eqalign{ A \cdot \left[\matrix{a_1 \cr a_2 \cr \vdots \cr a_n \cr}\right] & = \left[\matrix{0 \cr 0 \cr \vdots \cr 0 \cr}\right] \cr A^{-1} A \cdot \left[\matrix{a_1 \cr a_2 \cr \vdots \cr a_n \cr}\right] & = A^{-1} \cdot \left[\matrix{0 \cr 0 \cr \vdots \cr 0 \cr}\right] \cr \left[\matrix{a_1 \cr a_2 \cr \vdots \cr a_n \cr}\right] & = \left[\matrix{0 \cr 0 \cr \vdots \cr 0 \cr}\right] \cr}$$

Since $a_1 = a_2 = \cdots = a_n = 0$ , the functions are independent.

Example. $C^2(\real)$ denotes the vector space over $\real$ consisting of twice-differentiable functions $\real \to \real$ . Demonstrate that the set of functions $\{x, x^3, x^5\}$ is independent in $C^2(\real)$ .

Compute the Wronskian:

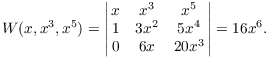
$$W(x, x^3, x^5) = \left|\matrix{ x & x^3 & x^5 \cr 1 & 3 x^2 & 5 x^4 \cr 0 & 6 x & 20 x^3 \cr}\right| = 16 x^6.$$

I can find values of x for which the Wronskian is nonzero: for example, if $x = 1$ , then $W(x, x^3, x^5) = 16 \ne 0$ . Hence, $\{x, x^3, x^5\}$ is independent.

The next example shows that the converse of the last theorem is false: You can have a set of independent functions whose Wronskian is always 0 (so there's no point where the Wronskian is nonzero).

Example. $C^1(\real)$ denotes the vector space over $\real$ consisting of differentiable functions $\real \to \real$ . Let

$$f(x) = x^2, \quad g(x) = \cases{x^2 & if $x \ge 0$ \cr -x^2 & if $x < 0$ \cr}.$$

Show that $\{f, g\}$ is independent in $C^1(\real)$ , but $W(f, g)(x) = 0$ for all $x \in \real$ .

Note: You can check that g is differentiable at 0, and $g'(0) = 0$ .

For independence, suppose that $a, b \in \real$ and $a f(x) + b g(x) = 0$ for all $x \in \real$ . Plugging in $x = 1$ , I get

$$\eqalign{ a f(1) + b g(1) & = 0 \cr a + b & = 0 \cr}$$

Plugging in $x = -1$ (and noting that $g(-1) = -(-1)^2 = -1$ ), I get

$$\eqalign{ a f(-1) + b g(-1) & = 0 \cr a - b & = 0 \cr}$$

Adding $a + b = 0$ and $a - b = 0$ gives $2 a = 0$ , so $a = 0$ . Plugging $a = 0$ into $a + b = 0$ gives $b = 0$ . This proves that $\{f, g\}$ is independent.

The Wronskian is

$$W(f, g)(x) = \left|\matrix{ f(x) & g(x) \cr f'(x) & g'(x) \cr}\right|.$$

I'll take cases.

Since $f(0) = 0$ and $g(0) = 0$ , I have $W(f, g)(0) = 0$ .

If $x > 0$ , I have $f'(x) = 2 x$ and $g'(x) = 2 x$ , so

$$W(f, g)(x) = \left|\matrix{ x^2 & x^2 \cr 2 x & 2 x \cr}\right| = 0.$$

If $x < 0$ , I have $f'(x) = 2 x$ and $g'(x) = -2 x$ , so

$$W(f, g)(x) = \left|\matrix{ x^2 & -x^2 \cr 2 x & -2 x \cr}\right| = 0.$$

This shows that $W(f, g)(x) = 0$ for all $x \in \real$ .

Contact information

Bruce Ikenaga's Home Page

Copyright 2022 by Bruce Ikenaga