The Exponential of a Matrix

In this section, all of the matrices will be real or complex matrices.

The solution to the exponential growth equation

$$\der y t = k y \quad \hbox{is given by} \quad y = c_0 e^{k t}.$$

A constant coefficient linear system has a similar form, but we have vectors and a matrix instead of scalars:

$$y' = A y.$$

Thus, if A is an $n \times n$ real matrix, then $y = (y_1, y_2, \ldots, y_n)$ .

It's natural to ask whether you can solve a constant coefficient linear system using some kind of exponential, as with the exponential growth equation.

If a solution to the system is to have the same form as the growth equation solution, it should look like

$$y = e^{A t} y_0.$$

But "$e^{A t}$ " seems to be e raised to a matrix power! How does that make any sense? It turns out that the matrix exponential $e^{A t}$ can be defined in a reasonable way.

From calculus, the Taylor series for $e^z$ is

$$e^z = \sum_{n = 0}^\infty \dfrac{z^n}{n!}.$$

It converges absolutely for all z.

It A is an $n \times n$ matrix with real entries, define

$$e^{A t} = \sum_{n = 0}^\infty \dfrac{t^n A^n}{n!}.$$

The powers $A^n$ make sense, since A is a square matrix. It is possible to show that this series converges for all t and every matrix A.

As a consequence, I can differentiate the series term-by-term:

$$\der {} t e^{A t} = \sum_{n = 0}^\infty n \dfrac{t^{n-1} A^n}{n!} = \sum_{n = 1}^\infty \dfrac{t^{n-1} A^n}{(n - 1)!} = A \sum_{n = 1}^\infty \dfrac{t^{n-1} A^{n-1}}{(n - 1)!} = A \sum_{m=0}^\infty \dfrac{t^m A^m}{m!} = A e^{A t}.$$

This shows that $e^{A t}$ solves the differential equation $y' = A y$ . The initial condition vector $y(0) = y_0$ yields the particular solution

$$y = e^{A t} y_0.$$

This works, because $e^{0 \cdot A} = I$ (by setting $t = 0$ in the power series).

Another familiar property of ordinary exponentials holds for the matrix exponential: If A and B commute (that is, $A B = B A$ ), then

$$e^{A} e^{B} = e^{A + B}.$$

You can prove this by multiplying the power series for the exponentials on the left. ($e^A$ is just $e^{A t}$ with $t = 1$ .)

Example. Compute $e^{A t}$ if

$$A = \left[\matrix{2 & 0 \cr 0 & 3 \cr}\right].$$

Compute the successive powers of A:

$$A = \left[\matrix{2 & 0 \cr 0 & 3 \cr}\right], \quad A^2 = \left[\matrix{4 & 0 \cr 0 & 9 \cr}\right], \quad \ldots , A^n = \left[\matrix{2^n & 0 \cr 0 & 3^n \cr}\right].$$

Therefore,

$$e^{A t} = \sum_{n = 0}^\infty \dfrac{t^n}{n!} \left[\matrix{2^n & 0 \cr 0 & 3^n \cr}\right] = \left[\matrix{\sum_{n = 0}^\infty \dfrac{(2 t)^n}{n!} & 0 \cr \noalign{\vskip2 pt} 0 & \sum_{n = 0}^\infty \dfrac{(3 t)^n}{n!} \cr}\right] = \left[\matrix{e^{2 t} & 0 \cr 0 & e^{3 t} \cr}\right].\quad\halmos$$

You can compute the exponential of an arbitrary diagonal matrix in the same way:

$$A = \left[\matrix{\lambda_1 & 0 & \cdots & 0 \cr 0 & \lambda_2 & \cdots & 0 \cr \vdots & \vdots & & \vdots \cr 0 & 0 & \cdots & \lambda_n \cr}\right], \quad e^{A t} = \left[\matrix{e^{\lambda_1 t} & 0 & \cdots & 0 \cr 0 & e^{\lambda_2 t} & \cdots & 0 \cr \vdots & \vdots & & \vdots \cr 0 & 0 & \cdots & e^{\lambda_n t} \cr}\right].$$

For example, if

$$A = \left[\matrix{ -3 & 0 & 0 \cr 0 & 4 & 0 \cr 0 & 0 & 1.73 \cr}\right], \quad\hbox{then}\quad e^{A t} = \left[\matrix{ e^{-3 t} & 0 & 0 \cr 0 & e^{4 t} & 0 \cr 0 & 0 & e^{1.73 t} \cr}\right].$$

Using this idea, we can compute $e^{A t}$ when A is diagonalizable. First, I'll give examples where we can compute $e^{A t}$ : First, using a "lucky" pattern, and second, using our knowledge of how to solve a system of differential equations.

Example. Compute $e^{A t}$ if

$$A = \left[\matrix{1 & 2 \cr 0 & 1 \cr}\right].$$

Compute the successive powers of A:

$$A = \left[\matrix{1 & 2 \cr 0 & 1 \cr}\right], \quad A^2 = \left[\matrix{1 & 4 \cr 0 & 1 \cr}\right], \quad A^3 = \left[\matrix{1 & 6 \cr 0 & 1 \cr}\right], \quad \ldots , A^n = \left[\matrix{1 & 2 n \cr 0 & 1 \cr}\right].$$

Hence,

$$e^{A t} = \sum_{n = 0}^\infty \dfrac{t^n}{n!} \left[\matrix{1 & 2 n \cr 0 & 1 \cr}\right] = \left[\matrix{\sum_{n = 0}^\infty \dfrac{t^n}{n!} & \sum_{n = 0}^\infty \dfrac{2 n t^n}{n!} \cr \noalign{\vskip2 pt} 0 & \sum_{n = 0}^\infty \dfrac{t^n}{n!} \cr}\right] = \left[\matrix{e^t & 2 t e^t \cr 0 & e^t \cr}\right].$$

Here's where the last equality came from:

$$\sum_{n = 0}^\infty \dfrac{t^n}{n!} = e^t,$$

$$\sum_{n = 0}^\infty \dfrac{2 n t^n}{n!} = 2 t \sum_{n = 1}^\infty \dfrac{t^{n-1}}{(n - 1)!} = 2 t \sum_{m=0}^\infty \dfrac{t^m}{m!} = 2 t e^t.\quad\halmos$$

In the last example, we got lucky in being able to recognize a pattern in the terms of the power series. Here is what happens if we aren't so lucky.

Example. Compute $e^{A t}$ , if

$$A = \left[\matrix{3 & -10 \cr 1 & -4 \cr}\right].$$

If you compute powers of A as in the last two examples, there is no evident pattern:

$$A^2 = \left[\matrix{-1 & 10 \cr -1 & 6 \cr}\right], \quad A^3 = \left[\matrix{7 & -30 \cr 3 & -14 \cr}\right], \quad A^4 = \left[\matrix{-9 & 50 \cr -5 & 26 \cr}\right], \ldots .$$

It looks like it would be difficult to compute the matrix exponential using the power series.

I'll use the fact that $e^{A t}$ is the solution to a linear system. The system's coefficient matrix is A, so the system is

$$\eqalign{ x' & = 3 x - 10 y \cr y' & = x - 4 y \cr}$$

You can solve this system by hand. For instance, the first equation gives

$$y = -\dfrac{1}{10} x' + \dfrac{3}{10} x \quad\hbox{so}\quad y' = -\dfrac{1}{10} x'' + \dfrac{3}{10} x'.$$

Plugging these expressions for y and $y'$ into $y' = x - 4 y$ , I get

$$-\dfrac{1}{10} x'' + \dfrac{3}{10} x' = x - 4 \left(-\dfrac{1}{10} x' + \dfrac{3}{10} x\right).$$

After some simplification, this becomes

$$x'' + x' - 2 x = 0.$$

The solution is

$$x = c_1 e^t + c_2 e^{-2 t}.$$

Plugging this into the expression for y above and doing some ugly algebra gives

$$y = \dfrac{1}{5} c_1 e^t + \dfrac{1}{2} c_2 e^{-2 t}.$$

Next, remember that if B is a $2 \times 2$ matrix,

$$B \left[\matrix{1 \cr 0 \cr}\right] = \hbox{first column of B} \quad\hbox{and}\quad B \left[\matrix{0 \cr 1 \cr}\right] = \hbox{second column of B}.$$

Try this out with a particular B to see how it works.

In particular, this is true for $e^{A t}$ . Now $x = e^{A t} x_0$ is the solution satisfying $x(0) = x_0$ , but

$$x = \left[\matrix{ c_1 e^t + c_2 e^{-2 t} \cr \noalign{\vskip2 pt} \dfrac{1}{5} c_1 e^t + \dfrac{1}{2} c_2 e^{-2 t} \cr}\right].$$

Set $x(0) = (1, 0)$ to get the first column of $e^{A t}$ :

$$\left[\matrix{1 \cr 0 \cr}\right] = \left[\matrix{ c_1 + c_2 \cr \noalign{\vskip2 pt} \dfrac{1}{5} c_1 + \dfrac{1}{2} c_2 \cr}\right].$$

Solving this system of equations for $c_1$ and $c_2$ , I get $c_1 = \dfrac{5}{3}$ , $c_2 = -\dfrac{2}{3}$ . So

$$\left[\matrix{x \cr y \cr}\right] = \left[\matrix{ \dfrac{5}{3} e^t - \dfrac{2}{3} e^{-2 t} \cr \noalign{\vskip2 pt} \dfrac{1}{3} e^t - \dfrac{1}{3} e^{-2 t} \cr}\right].$$

Set $x(0) = (0, 1)$ to get the second column of $e^{A t}$ :

$$\left[\matrix{0 \cr 1 \cr}\right] = \left[\matrix{ c_1 + c_2 \cr \noalign{\vskip2 pt} \dfrac{1}{5} c_1 + \dfrac{1}{2} c_2 \cr}\right].$$

Therefore, $c_1 = -\dfrac{10}{3}$ , $c_2 = \dfrac{10}{3}$ . Hence,

$$\left[\matrix{x \cr y \cr}\right] = \left[\matrix{ -\dfrac{10}{3} e^t + \dfrac{10}{3} e^{-2 t} \cr \noalign{\vskip2 pt} -\dfrac{2}{3} e^t + \dfrac{5}{3} e^{-2 t} \cr}\right].$$

Therefore,

$$e^{A t} = \left[\matrix{ \dfrac{5}{3} e^t - \dfrac{2}{3} e^{-2 t} & -\dfrac{10}{3} e^t + \dfrac{10}{3} e^{-2 t} \cr \noalign{\vskip2 pt} \dfrac{1}{3} e^t - \dfrac{1}{3} e^{-2 t} & -\dfrac{2}{3} e^t + \dfrac{5}{3} e^{-2 t} \cr}\right].$$

So I found $e^{A t}$ , but this was a lot of work (not all of which I wrote out!), and A was just a $2 \times 2$ matrix.

We noted earlier that we can compute $e^{A t}$ fairly easily in case A is diagonalizable. Recall that an $n \times n$ matrix A is diagonalizable if it has n independent eigenvectors. (This is true, for example, if A has n distinct eigenvalues.)

Suppose A is diagonalizable with independent eigenvectors $v_1, \ldots, v_n$ and corresponding eigenvalues $\lambda_1, \ldots, \lambda_n$ . Let S be the matrix whose columns are the eigenvectors:

$$S = \left[\matrix{ \uparrow & \uparrow & & \uparrow \cr v_1 & v_2 & \cdots & v_n \cr \downarrow & \downarrow & & \downarrow \cr}\right].$$

Then

$$S^{-1} A S = \left[\matrix{ \lambda_1 & 0 & \cdots & 0 \cr 0 & \lambda_2 & \cdots & 0 \cr \vdots & \vdots & & \vdots \cr 0 & 0 & \cdots & \lambda_n \cr}\right] = D.$$

We saw earlier how to compute the exponential for the diagonal matrix D:

$$e^{D t} = \left[\matrix{ e^{\lambda_1 t} & 0 & \cdots & 0 \cr 0 & e^{\lambda_2 t} & \cdots & 0 \cr \vdots & \vdots & & \vdots \cr 0 & 0 & \cdots & e^{\lambda_n t} \cr}\right].$$

But note that

$$\eqalign{ (S^{-1} A S)^2 & = (S^{-1} A S)(S^{-1} A S) = S^{-1} A^2 S \cr (S^{-1} A S)^3 & = (S^{-1} A S)(S^{-1} A S)(S^{-1} A S) = S^{-1} A^3 S \cr}$$

Notice how each "$S S^{-1}$ " pair cancels. Continuing in this way --- you can give a formal proof using induction --- we have $(S^{-1} A S)^n = S^{-1} A^n S$ . Therefore,

$$e^{D t} = \sum_{n = 0}^\infty \dfrac{t^n (S^{-1} A S)^n}{n!} = S^{-1} \left(\sum_{n = 0}^\infty \dfrac{t^n A^n}{n!}\right) S = S^{-1} e^{A t} S.$$

Then

$$\eqalign{ S e^{D t} S^{-1} & = S S^{-1} e^{A t} S S^{-1} \cr S e^{D t} S^{-1} & = e^{A t} \cr}$$

Notice that S and $S^{-1}$ have "switched places" from the original diagonalization equation.

Hence,

$$e^{A t} = S \left[\matrix{ e^{\lambda_1 t} & 0 & \cdots & 0 \cr 0 & e^{\lambda_2 t} & \cdots & 0 \cr \vdots & \vdots & & \vdots \cr 0 & 0 & \cdots & e^{\lambda_n t} \cr}\right] S^{-1}.$$

Thus, if A is diagonalizable, find the eigenvalues and use them to construct the diagonal matrix with the exponentials in the middle. Find a set of independent eigenvectors and use them to construct S and $S^{-1}$ . Putting everything into the equation above gives $e^{A t}$ .

Example. Compute $e^{A t}$ if

$$A = \left[\matrix{3 & 5 \cr 1 & -1 \cr}\right].$$

The characteristic polynomial is $(x - 4)(x + 2)$ and the eigenvalues are $\lambda = 4$ , $\lambda = -2$ . Since there are two different eigenvalues and A is a $2 \time 2$ matrix, A is diagonalizable. The corresponding eigenvectors are $(5, 1)$ and $(-1, 1)$ . Thus,

$$S = \left[\matrix{ 5 & -1 \cr 1 & 1 \cr}\right], \quad S^{-1} = \dfrac{1}{6} \left[\matrix{ 1 & 1 \cr -1 & 5 \cr}\right].$$

Hence,

$$e^{A t} = \left[\matrix{5 & -1 \cr 1 & 1 \cr}\right] \left[\matrix{e^{4 t} & 0 \cr 0 & e^{-2 t} \cr}\right] \left(\dfrac{1}{6}\right) \left[\matrix{1 & 1 \cr -1 & 5 \cr}\right] = \dfrac{1}{6} \left[\matrix{ 5 e^{4 t} + e^{-2 t} & 5 e^{4 t} - 5 e^{-2 t} \cr e^{4 t} - e^{-2 t} & e^{4 t} + 5 e^{-2 t} \cr}\right].\quad\halmos$$

Example. Compute $e^{A t}$ if

$$A = \left[\matrix{ 5 & -6 & -6 \cr -1 & 4 & 2 \cr 3 & -6 & -4 \cr}\right].$$

The characteristic polynomial is $(x - 1)(x - 2)^2$ and the eigenvalues are $\lambda = 1$ and $\lambda = 2$ (a double root). The corresponding eigenvectors are $(3, -1, 3)$ for $\lambda = 1$ , and $(2, 1, 0)$ and $(2, 0, 1)$ for $\lambda = 2$ . Since I have 3 independent eigenvectors, the matrix is diagonalizable.

I have

$$S = \left[\matrix{ 3 & 2 & 2 \cr -1 & 1 & 0 \cr 3 & 0 & 1 \cr}\right], \quad S^{-1} = \left[\matrix{ -1 & 2 & 2 \cr -1 & 3 & 2 \cr 3 & -6 & -5 \cr}\right].$$

From this, it follows that

$$e^{A t} = \left[\matrix{ -3 e^t + 4 e^{2 t} & 6 e^t - 6 e^{2 t} & 6 e^t - 6 e^{2 t} \cr e^t - e^{2 t} & -2 e^t + 3 e^{2 t} & -2 e^t + 2 e^{2 t} \cr -3 e^t + 3 e^{2 t} & 6 e^t - 6 e^{2 t} & 6 e^t - 5 e^{2 t} \cr}\right].\quad\halmos$$

Here's a quick check you can use when computing $e^{A t}$ . Plugging $t = 0$ into $e^{A t}$ gives $e^0 = I$ , the identity matrix. For instance, in the last example, if you set $t = 0$ in the right side, it checks:

$$\left[\matrix{ 1 & 0 & 0 \cr 0 & 1 & 0 \cr 0 & 0 & 1 \cr}\right].$$

However, this check isn't foolproof --- just because you get I by setting $t = 0$ doesn't mean your answer is right. However, if you don't get I, your answer is surely wrong!

A better check that is a little more work is to compute the derivative of $e^{A t}$ , and then set $t = 0$ . You should get A. To see this, note that

$$\der {} t e^{A t} = A e^{A t}.$$

Evaluating both sides of this equation at $t = 0$ gives $\left. \der {} t e^{A t}\right|_{t = 0} = A$ . Since the theory of differential equations tells us that the solution to an initial value problem of this kind is unique, if your answer passes these checks then it is $e^{A t}$ . I think it's good to do the first (easier) check, even if you don't do the second.

If you try this in the previous example, you'll find that the second check works as well.

Unfortunately, not every matrix is diagonalizable. How do we compute $e^{A t}$ for an arbitrary real matrix?

One approach is to use the Jordan canonical form for a matrix, but this would require a discussion of canonical forms, a large subject in itself.

Note that any method for finding $e^{A t}$ requires finding the eigenvalues of A which is, in general, a difficult problem. For instance, there are methods from numerical analysis for approximating the eigenvalues of a matrix.

I'll describe an iterative algorithm for computing $e^{A t}$ that only requires that one know the eigenvalues of A. There are various such algorithms for computing the matrix exponential; this one, which is due to Richard Williamson [1], seems to me to be the easiest for hand computation. It's also possible to implement this method using a computer algebra system like maxima or Mathematica.

Let A be an $n \times n$ matrix. Let $\{\lambda_1, \lambda_2, \ldots, \lambda_n\}$ be a list of the eigenvalues, with multiple eigenvalues repeated according to their multiplicity.

The last phrase means that if the characteristic polynomial is $(x - 1)^3 (x - 5)$ , the eigenvalue 1 is listed 3 times. So your list of eigenvalues might be $\{1, 1, 1, 5\}$ . But you can list them in any order; if you wanted to show off, you could make your list $\{1, 5, 1, 1\}$ . It will probably make the computations easier and less error-prone if you list the eigenvalues in some "nice" way (so either $\{1, 1, 1, 5\}$ or $\{5, 1, 1, 1\}$ ).

Let

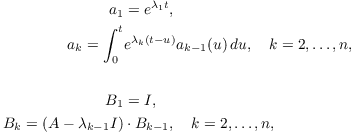
$$\eqalign{ a_1 & = e^{\lambda_1 t},\cr a_k = \int_0^t & e^{\lambda_k (t - u)} a_{k-1}(u)\,du, \quad k = 2, \ldots, n,\cr & \cr B_1 & = I,\cr B_k = (A - \lambda_{k-1} I) & \cdot B_{k-1}, \quad k = 2, \ldots, n,\cr}$$

Then

$$e^{A t} = a_1 B_1 + a_2 B_2 + \ldots + a_n B_n.$$

Remark. If you've seen convolutions before, you might recognize that the expression for $a_k$ is a convolution:

$$a_k = e^{\lambda_k t} \star a_{k-1}(t).$$

In general, the convolution of f and g is

$$(f \star g)(t) = \int_0^t f(t - u) g(u)\,du.$$

If you haven't seen this before, don't worry: you do not need to know this! The important thing (which gives the definition of $a_k$ ) is the integral on the right side.

To prove that this algorithm works, I'll show that the expression on the right satisfies the differential equation $x' = A x$ . To do this, I'll need two facts about the characteristic polynomial $p(x)$ .

1. $(x - \lambda_1)(x - \lambda_2)\cdots (x - \lambda_n) = p(x)$ .

2. ( Cayley-Hamilton Theorem) $p(A) = 0$ .

Observe that if $p(x)$ is the characteristic polynomial, then using the first fact and the definition of the B's,

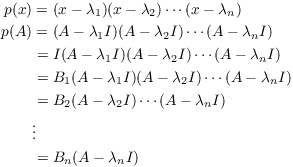
$$\eqalign{ p(x) & = (x - \lambda_1)(x - \lambda_2) \cdots (x - \lambda_n) \cr p(A) & = (A - \lambda_1 I)(A - \lambda_2 I) \cdots (A - \lambda_n I) \cr & = I(A - \lambda_1 I)(A - \lambda_2 I) \cdots (A - \lambda_n I) \cr & = B_1 (A - \lambda_1 I)(A - \lambda_2 I) \cdots (A - \lambda_n I) \cr & = B_2 (A - \lambda_2 I) \cdots (A - \lambda_n I) \cr & \vdots \cr & = B_n (A - \lambda_n I) \cr}$$

By the Cayley-Hamilton Theorem,

$$B_n (A - \lambda_n I) = 0. \eqno{(*)}$$

I will use this fact in the proof below. First, let's see an example of the Cayley-Hamilton theorem. Let

$$A = \left[\matrix{2 & 3 \cr 2 & 1 \cr}\right].$$

The characteristic polynomial is $(x - 2)(x - 1) - 6 = x^2 - 3 x - 4$ . The Cayley-Hamilton theorem asserts that if you plug A into $x^2 - 3 x - 4$ , you'll get the zero matrix.

First,

$$A^2 = \left[\matrix{2 & 3 \cr 2 & 1 \cr}\right] \left[\matrix{2 & 3 \cr 2 & 1 \cr}\right] = \left[\matrix{10 & 9 \cr 6 & 7 \cr}\right].$$

Therefore,

$$A^2 - A - 4 I = \left[\matrix{10 & 9 \cr 6 & 7 \cr}\right] - \left[\matrix{6 & 9 \cr 6 & 3 \cr}\right] - \left[\matrix{4 & 0 \cr 0 & 4 \cr}\right] = \left[\matrix{0 & 0 \cr 0 & 0 \cr}\right].\quad\halmos$$

We've verified the Cayley-Hamilton theorem for this matrix. We'll provide a proof elsewhere. Let's give a proof of the algorithm for $e^{A t}$ .

Proof of the algorithm. First,

$$a_k = \int_0^t e^{\lambda_k (t - u)} a_{k-1}(u)\,du = e^{\lambda_k t} \int_0^t e^{-\lambda_k u} a_{k-1}(u)\,du.$$

Recall that the Fundamental Theorem of Calculus says that

$$\der {} t \int _0^t f(u)\,du = f(t).$$

Applying this and the Product Rule, I can differentiate $a_k$ to obtain

$$a_k' = \lambda_k e^{\lambda_k t} \int_0^t e^{-\lambda_k u} a_{k-1}(u)\,du + e^{\lambda_k t} e^{-\lambda_k t} a_{k-1}(t),$$

$$a_k' = \lambda_k a_k + a_{k-1}.$$

Therefore,

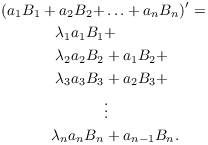
$$\eqalign{ (a_1 B_1 + a_2 B_2 + &\ldots + a_n B_n)' = \cr \lambda_1 a_1 B_1 &+ \cr \lambda_2 a_2 B_2 &+ a_1 B_2 + \cr \lambda_3 a_3 B_3 &+ a_2 B_3 + \cr &\vdots \cr \lambda_n a_n B_n &+ a_{n-1} B_n.}$$

Expand the $a_{i-1} B_i$ terms using

$$a_{i-1} B_i = a_{i-1}(A - \lambda_{i-1}I)B_{i-1} = a_{i-1} A B_{i-1} - \lambda_{i-1} a_{i-1} B_{i-1}.$$

Making this substitution and telescoping the sum, I have

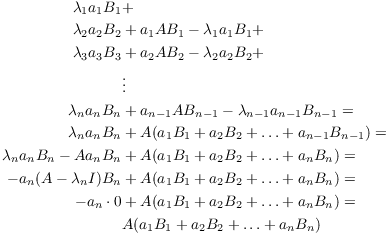
$$\eqalign{ \lambda_1 a_1 B_1 & + \cr \lambda_2 a_2 B_2 & + a_1 A B_1 - \lambda_1 a_1 B_1 + \cr \lambda_3 a_3 B_3 & + a_2 A B_2 - \lambda_2 a_2 B_2 + \cr &\vdots \cr \lambda_n a_n B_n & + a_{n-1} A B_{n-1} - \lambda_{n-1} a_{n-1} B_{n-1} = \cr \lambda_n a_n B_n & + A(a_1 B_1 + a_2 B_2 + \ldots + a_{n-1} B_{n-1}) = \cr \lambda_n a_n B_n - A a_n B_n & + A(a_1 B_1 + a_2 B_2 + \ldots + a_n B_n) = \cr -a_n(A - \lambda_n I)B_n & + A(a_1 B_1 + a_2 B_2 + \ldots + a_n B_n) = \cr -a_n \cdot 0 & + A(a_1 B_1 + a_2 B_2 + \ldots + a_n B_n) = \cr & A(a_1 B_1 + a_2 B_2 + \ldots + a_n B_n) \cr}$$

(The result (*) proved above was used in the next-to-the-last equality.) Combining the results above, I've shown that

$$(a_1 B_1 + a_2 B_2 + \ldots + a_n B_n)' = A(a_1 B_1 + a_2 B_2 + \ldots + a_n B_n).$$

This shows that $M = a_1 B_1 + a_2 B_2 + \ldots + a_n B_n$ satisfies $M' = A M$ .

Using the power series expansion, I have $e^{-A t} A = A e^{-A t}$ . So

$$(e^{-A t} M)' = -A e^{-A t} M + e^{-A t} A M = -e^{-A t} A M + e^{-A t} A M = 0.$$

(Remember that matrix multiplication is not commutative in general!) It follows that $e^{-A t} M$ is a constant matrix.

Set $t = 0$ . Since $a_2 = \cdots = a_n = 0$ , it follows that $M(0) = I$ . In addition, $e^{-A \cdot 0} = I$ . Therefore, $e^{-A t} M = I$ , and hence $M = e^{A t}$ .

Example. Use the matrix exponential to solve

$$y' = \left[\matrix{3 & -1 \cr 1 & 1 \cr}\right] y, \qquad y(0) = \left[\matrix{3 \cr 4 \cr}\right].$$

$y = (y_1, y_2)$ is the solution vector.

The characteristic polynomial is $(x - 2)^2$ . You can check that there is only one independent eigenvector, so I can't solve the system by diagonalizing. I could use generalized eigenvectors to solve the system, but I will use the matrix exponential to illustrate the algorithm.

First, list the eigenvalues: $\{2, 2\}$ . Since $\lambda = 2$ is a double root, it is listed twice.

First, I'll compute the $a_k$ 's:

$$a_1 = e^{2 t},$$

$$a_2 = e^{2 t} \star a_1(t) = \int_0^t e^{2(t - u)} e^{2 u}\,du = e^{2 t} \int_0^t du = te^{2 t}.$$

Here are the $B_k$ 's:

$$B_1 = I, \quad B_2 = (A - 2 I) B_1 = A - 2 I = \left[\matrix{1 & -1 \cr 1 & -1 \cr}\right].$$

Therefore,

$$e^{A t} = e^{2 t} \left[\matrix{1 & 0 \cr 0 & 1 \cr}\right] + t e^{2 t} \left[\matrix{1 & -1 \cr 1 & -1 \cr}\right] = \left[\matrix{e^{2 t} + t e^{2 t} & -t e^{2 t} \cr t e^{2 t} & e^{2 t} - t e^{2 t} \cr}\right].$$

As a rough check, note that setting $t = 0$ produces the identity.)

The solution to the given initial value problem is

$$y = \left[\matrix{e^{2 t} + t e^{2 t} & -t e^{2 t} \cr t e^{2 t} & e^{2 t} - t e^{2 t} \cr}\right] \left[\matrix{3 \cr 4 \cr}\right].$$

You can get the general solution by replacing $(3, 4)$ with $(c_1, c_2)$ .

Example. Find $e^{A t}$ if

$$A = \left[\matrix{ 1 & 0 & 0 \cr 1 & 1 & 0 \cr -1 & -1 & 2 \cr}\right].$$

The eigenvalues are obviously $\lambda = 1$ (double) and $\lambda = 2$ .

First, I'll compute the $a_k$ 's. I have $a_1 = e^t$ , and

$$a_2 = \int_0^t e^{t - u} e^u\,du = e^t \int_0^t\,du = te^t,$$

$$a_3 = \int_0^t e^{2(t - u)} ue^u\,du = -te^t - e^t + e^{2 t}.$$

Next, I'll compute the $B_k$ 's. $B_1 = I$ , and

$$B_2 = A - I = \left[\matrix{ 0 & 0 & 0 \cr 1 & 0 & 0 \cr -1 & -1 & 1 \cr}\right],$$

$$B_3 = (A - I)B_2 = \left[\matrix{ 0 & 0 & 0 \cr 0 & 0 & 0 \cr -2 & -1 & 1 \cr}\right].$$

Therefore,

$$e^{A t} = \left[\matrix{ e^t & 0 & 0 \cr t e^t & e^t & 0 \cr t e^t + 2 e^t - 2 e^{2 t} & e^t - e^{2 t} & e^{2 t} \cr}\right].\quad\halmos$$

Example. Use the matrix exponential to solve

$$y' = \left[\matrix{2 & -5 \cr 2 & -4 \cr}\right] y.$$

$y = (y_1, y_2)$ is the solution vector.

This example will demonstrate how the algorithm for $e^{A t}$ works when the eigenvalues are complex.

The characteristic polynomial is $x^2 + 2 x + 2$ . The eigenvalues are $\lambda = -1 \pm i$ . I will list them as $\{-1 + i, -1 - i\}$ .

First, I'll compute the $a_k$ 's. $a_1 = e^{(-1 + i)t}$ , and

$$a_2 = \int_0^t e^{(-1 + i)(t - u)} e^{(-1 - i)u}\,du = e^{(-1 + i)t} \int_0^t e^{(1 - i)u} e^{(-1 - i)u}\,du =$$

$$e^{(-1 + i)t} \int_0^t e^{-2 i u}\,du = e^{(-1 + i)t} \dfrac{i}{2} \left(e^{-2 i t} - 1\right) = \dfrac{i}{2} \left(e^{(-1 - i)t} - e^{(-1 + i)t}\right).$$

Next, I'll compute the $B_k$ 's. $B_1 = I$ , and

$$B_2 = A - (-1 + i)I = \left[\matrix{3 - i & -5 \cr 2 & -3 - i \cr}\right].$$

Therefore,

$$e^{A t} = e^{(-1 + i)t} \left[\matrix{ 1 & 0 \cr 0 & 1 \cr}\right] + \dfrac{i}{2} \left(e^{(-1 - i)t} - e^{(-1 + i)t}\right) \left[\matrix{ 3 - i & -5 \cr 2 & -3 - i \cr}\right].$$

I want a real solution, so I'll use DeMoivre's Formula to simplify:

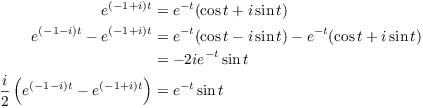
$$\eqalign{ e^{(-1 + i)t} & = e^{-t} (\cos t + i \sin t) \cr e^{(-1 - i)t} - e^{(-1 + i)t} & = e^{-t} (\cos t - i \sin t) - e^{-t} (\cos t + i \sin t) \cr & = - 2 i e^{-t} \sin t \cr \dfrac{i}{2} \left(e^{(-1 - i)t} - e^{(-1 + i)t}\right) & = e^{-t} \sin t \cr}$$

Plugging these into the expression for $e^{A t}$ above, I have

$$e^{A t} = e^{-t} (\cos t + i \sin t) \left[\matrix{ 1 & 0 \cr 0 & 1 \cr}\right] + e^{-t} \sin t \left[\matrix{ 3 - i & -5 \cr 2 & -3 - i \cr}\right] = e^{-t} \left[\matrix{ \cos t + 3 \sin t & -5 \sin t \cr 2 \sin t & \cos t - 3 \sin t \cr}\right].$$

Notice that all the i's have dropped out! This reflects the obvious fact that the exponential of a real matrix must be a real matrix.

Finally, the general solution to the original system is

$$y = e^{-t}\left[\matrix{\cos t + 3 \sin t & -5 \sin t \cr 2 \sin t & \cos t - 3 \sin t \cr}\right] \left[\matrix{c_1 \cr c_2 \cr}\right].\quad\halmos$$

Example. Solve the following system using both the matrix exponential and the eigenvector methods.

$$y' = \left[\matrix{ 2 & -1 \cr 1 & 2 \cr}\right] y.$$

$y = (y_1, y_2)$ is the solution vector.

The characteristic polynomial is $x^2 - 4 x + 5$ . The eigenvalues are $\lambda = 2 \pm i$ .

Consider $\lambda = 2 + i$ :

$$A - (2 + i)I = \left[\matrix{ -i & -1 \cr 1 & -i \cr}\right].$$

As this is an eigenvector matrix, it must be singular, and hence the rows must be multiples. So ignore the second row. I want a vector $(a, b)$ such that $(-i)a + (-1)b = 0$ . To get such a vector, switch the $-i$ and -1 and negate one of them: $a = 1$ , $b = -i$ . Thus, $(1, -i)$ is an eigenvector.

The corresponding solution is

$$e^{(2 + i)t} \left[\matrix{1 \cr -i \cr}\right] = e^{2 t} \left[\matrix{\cos t + i \sin t \cr \sin t - i \cos t \cr}\right].$$

Take the real and imaginary parts:

$$\re e^{(2 + i)t} \left[\matrix{1 \cr -i \cr}\right] = e^{2 t} \left[\matrix{\cos t \cr \sin t \cr}\right],$$

$$\im e^{(2 + i)t} \left[\matrix{1 \cr -i \cr}\right] = e^{2 t} \left[\matrix{\sin t \cr -\cos t \cr}\right].$$

The solution is

$$y = e^{2 t} \left(c_1 \left[\matrix{\cos t \cr \sin t \cr}\right] + c_2 \left[\matrix{\sin t \cr -\cos t \cr}\right]\right).$$

Now I'll solve the equation using the matrix exponential. The eigenvalues are $\{2 + i, 2 - i\}$ . Compute the $a_k$ 's. $a_1 = e^{(2 + i)t}$ , and

$$a_2 = e^{(2 - i)t}\star e^{(2 + i)t} = \int_0^t e^{(2 - i)(t - u)} e^{(2 + i)u}\,du = e^{(2 - i)t} \int_0^t e^{2 i u}\,du =$$

$$e^{(2 - i)t} \left[-\dfrac{i}{2} e^{2 iu}\right]_0^t = \dfrac{i}{2} e^{(2 - i)t} \left(1 - e^{2 i t}\right) = \dfrac{i}{2} e^{2 t}\left(e^{-i t} - e^{-i t}\right) = e^{2 t} \sin t.$$

(Here and below, I'm cheating a little in the comparison by not showing all the algebra involved in the simplification. You need to use DeMoivre's Formula to eliminate the complex exponentials.)

Next, compute the $B_k$ 's. $B_1 = I$ , and

$$B_2 = A - (2 + i)I = \left[\matrix{ -i & -1 \cr 1 & -i \cr}\right].$$

Therefore,

$$e^{A t} = e^{(2 + i)t} \left[\matrix{ 1 & 0 \cr 0 & 1 \cr}\right] + e^{2 t} \sin t \left[\matrix{ -i & -1 \cr 1 & -i \cr}\right] = e^{2 t} \left[\matrix{ \cos t & -\sin t \cr \sin t & \cos t \cr}\right].$$

The solution is

$$y = e^{2 t} \left[\matrix{ \cos t & -\sin t \cr \sin t & \cos t \cr}\right] \left[\matrix{c_1 \cr c_2 \cr}\right].$$

Taking into account some of the algebra I didn't show for the matrix exponential, I think the eigenvector approach is easier.

Example. Solve the following system using both the matrix exponential and the (generalized) eigenvector methods.

$$y' = \left[\matrix{5 & -8 \cr 2 & -3 \cr}\right] y.$$

$y = (y_1, y_2)$ is the solution vector.

I'll do this first using the generalized eigenvector method, then using the matrix exponential.

The characteristic polynomial is $x^2 - 2 x + 1$ . The eigenvalue is $\lambda = 1$ (double).

$$A - I = \left[\matrix{4 & -8 \cr 2 & -4 \cr}\right].$$

Ignore the first row, and divide the second row by 2, obtaining the vector $(1, -2)$ . I want $(a, b)$ such that $(1)a + (-2)b = 0$ . Swap 1 and -2 and negate the -2: I get $(a, b) = (2, 1)$ . This is an eigenvector for $\lambda = -1$ .

Since I only have one eigenvector, I need a generalized eigenvector. This means I need $(a', b')$ such that

$$\left[\matrix{4 & -8 \cr 2 & -4 \cr}\right] \left[\matrix{a' \cr b' \cr}\right] = \left[\matrix{2 \cr 1 \cr}\right].$$

Row reduce:

$$\left[\matrix{ 4 & -8 & 2 \cr 2 & -4 & 1 \cr}\right] \quad \to \quad \left[\matrix{ 1 & -2 & \dfrac{1}{2} \cr \noalign{\vskip2 pt} 0 & 0 & 0 \cr}\right]$$

This means that $a' = 2 b' + \dfrac{1}{2}$ . Setting $b' = 0$ yields $a' = \dfrac{1}{2}$ . The generalized eigenvector is $\left(\dfrac{1}{2}, 0\right)$ .

The solution is

$$y = c_1 e^t \left[\matrix{2 \cr 1 \cr}\right] + c_2\left(t e^t \left[\matrix{2 \cr 1 \cr}\right] + e^t \left[\matrix{\dfrac{1}{2} \cr \noalign{\vskip2 pt} 0 \cr}\right]\right).$$

Next, I'll solve the system using the matrix exponential. The eigenvalues are $\{1, 1\}$ . First, I'll compute the $a_k$ 's. $a_1 = e^t$ , and

$$a_2 = e^t \star e^t = \int_0^t e^{t - u} e^u\,du = e^t \int_0^t\,du = t e^t.$$

Next, compute the $B_k$ 's. $B_1 = I$ , and

$$B_2 = A - I = \left[\matrix{4 & -8 \cr 2 & -4 \cr}\right].$$

Therefore,

$$e^{A t} = e^t \left[\matrix{1 & 0 \cr 0 & 1 \cr}\right] + t e^t \left[\matrix{4 & -8 \cr 2 & -4 \cr}\right] = \left[\matrix{e^t + 4 t e^t & -8 t e^t \cr 2 t e^t & e^t - 4 t e^t \cr}\right].$$

The solution is

$$y = \left[\matrix{e^t + 4 t e^t & -8 t e^t \cr 2 t e^t & e^t - 4 t e^t \cr}\right] \left[\matrix{c_1 \cr c_2 \cr}\right].$$

In this case, finding the solution using the matrix exponential may be a little bit easier.

[1] Richard Williamson, Introduction to differential equations. Englewood Cliffs, NJ: Prentice-Hall, 1986.

Contact information

Bruce Ikenaga's Home Page

Copyright 2023 by Bruce Ikenaga