Properties of Matrix Arithmetic

I've given examples which illustrate how you can do arithmetic with matrices. Now I'll give precise definitions of the various matrix operations. This will allow me to prove some useful properties of these operations. If you look at the definitions, you'll see the ideas we showed earlier by example.

The proofs will probably look pretty abstract to you, somewhat like our earlier proofs for properties of number systems. How you approach them depends on what you intend to learn. If you're mainly interested in doing computations, you could skim these properties and definitions without worrying about the proofs. At least try to understand, by example if necessary, what they say. Get an idea of what kinds of manipulations "are allowed" with matrices.

If you're trying to learn this material in some depth (particularly if you intend to do more advanced math), try to read at least some of the proofs. Perhaps challenge yourself by trying to write some of the proofs yourself, for example the proofs that I've omitted.

If A is a matrix, the element in the $i^{\rm th}$ row and $j^{\rm th}$ column will be denoted $A_{ij}$ . (Sometimes I'll switch to lower-case letters and use $a_{ij}$ instead of $A_{ij}$ ). Thus,

$(A + B)_{ij}$ is the $(i, j)^{\rm th}$ entry of $A + B$ .

$(A B)_{ij}$ is the $(i, j)^{\rm th}$ entry of $AB$ .

$(A^T)_{ij}$ is the $(i, j)^{\rm th}$ entry of $A^T$ .

$(k A + B^T)_{ij}$ is the $(i, j)^{\rm th}$ entry of $k A + B^T$ .

Keep in mind that a thing with an "$ij$ " subscript is a number --- without the subscript, you have a matrix.

Remark. To avoid confusion, use a comma between the indices where appropriate. "$A_{24}$ " clearly means the entry in row 2, column 4. However, for the entry in row 13, column 6, write "$A_{13,6}$ ", not "$A_{136}$ ".

Here are the formal definitions of the matrix operations. When I write something like "for all i and j", you should take this to mean "for all i such that $1 \le i \le m$ , where m is the number of rows, and for all j such that $1 \le j \le n$ , where n is the number of columns".

Definition. ( Equality) Let A and B be matrices. Then $A = B$ if and only if A and B have the same dimensions and $a_{ij} = b_{ij}$ for all i and j.

This definition says that two matrices are equal if they have the same dimensions and corresponding entries are equal.

Definition. ( Sums and Differences) Let A and B be matrices. If A and B have the same dimensions, then the sum $A + B$ and the difference $A - B$ are defined, and their entries are given by

$$(A + B)_{ij} = A_{ij} + B_{ij} \quad\hbox{and}\quad (A - B)_{ij} = A_{ij} - B_{ij} \quad\hbox{for all}\quad i, j.$$

This definition says that if two matrices have the same dimensions, you can add or subtract them by adding or subtracting corresponding entries.

Definition. The $m \times n$ zero matrix 0 is the $m \times n$ matrix whose $(i, j)^{\rm th}$ entry is given by

$$0_{ij} = 0 \quad\hbox{for all}\quad i, j.$$

Proposition. Let A, B, and C be $m \times n$ matrices, and let 0 denote the $m \times n$ zero matrix. Then:

(a) ( Associativity of Addition)

$$(A + B) + C = A + (B + C).$$

(b) ( Commutativity of Addition)

$$A + B = B + A.$$

(c) ( Identity for Addition)

$$0 + A = A \quad\hbox{and}\quad A + 0 = A.$$

Remark. You'll see that the idea in many of these proofs for matrices is to reduce the proof to a known property of numbers (such as associativity or commutativity) by looking at the entries of the matrices. This is what the definition of equality of matrices allows us to do.

You can also see that the properties in this Proposition look "obvious" --- they are statements that you'd "expect" to be true, even if no one told you. That is typical for most of the material in this section, which is why you should not be intimidated by all the symbols.

Most of the proofs that follow are fairly simple. Hence, I won't write out all of them, and I won't always do them in step-by-step detail like the ones above.

Proof. Each of the properties is a matrix equation. The definition of matrix equality says that I can prove that two matrices are equal by proving that their corresponding entries are equal. I'll follow this strategy in each of the proofs that follows.

(a) To prove that $(A + B) + C = A + (B + C)$ , I have to show that their corresponding entries are equal:

$$\left((A + B) + C\right)_{ij} = \left(A + (B + C)\right)_{ij}.$$

(Do you understand what this says? $\left((A + B) + C\right)_{ij}$ is the $(i, j)^{\rm th}$ entry of $(A + B) + C$ , while $\left(A + (B + C)\right)_{ij}$ is the $(i, j)^{\rm th}$ entry of $A + (B + C)$ .)

Since this is the first proof of this kind that I've done, I'll show the justification for each step.

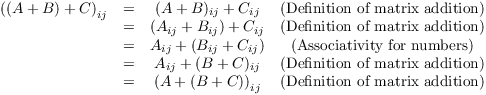
$$\matrix{ \left((A + B) + C\right)_{ij} & = & (A + B)_{ij} + C_{ij} & \hbox{(Definition of matrix addition)} \cr & = & (A_{ij} + B_{ij}) + C_{ij} & \hbox{(Definition of matrix addition)} \cr & = & A_{ij} + (B_{ij} + C_{ij}) & \hbox{(Associativity for numbers)} \cr & = & A_{ij} + (B + C)_{ij} & \hbox{(Definition of matrix addition)} \cr & = & \left(A + (B + C)\right)_{ij} & \hbox{(Definition of matrix addition)} \cr}$$

"Associativity" refers to associativity of addition for numbers.

Therefore, $(A + B) + C = A + (B + C)$ , because their corresponding elements are equal.

(b) To prove that $A + B = B + A$ , I have to show that their corresponding entries are equal:

$$(A + B)_{ij} = (B + A)_{ij}.$$

By definition of matrix addition,

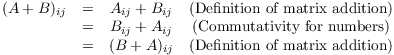
$$\matrix{ (A + B)_{ij} & = & A_{ij} + B_{ij} & \hbox{(Definition of matrix addition)} \cr & = & B_{ij} + A_{ij} & \hbox{(Commutativity for numbers)} \cr & = & (B + A)_{ij} & \hbox{(Definition of matrix addition)} \cr}$$

"Commutativity" refers to commutativity of addition of numbers.

Therefore,

$$A + B = B + A.$$

(c) To prove that $A + 0 = A$ , I have to show that their corresponding entries are equal:

$$(A + 0)_{ij} = A_{ij}.$$

By definition of matrix addition and the zero matrix,

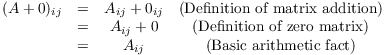
$$\matrix{ (A + 0)_{ij} & = & A_{ij} + 0_{ij} & \hbox{(Definition of matrix addition)} \cr & = & A_{ij} + 0 & \hbox{(Definition of zero matrix)} \cr & = & A_{ij} & \hbox{(Basic arithmetic fact)} \cr}$$

"Basic arithmetic fact" refers to the fact that if x is a number, then $x + 0 = x$ .

Therefore, $A + 0 = A$ .

In part (b), I showed that addition is commutative. Therefore,

$$0 + A = A + 0 = A.\quad\halmos$$

Definition. ( Multiplication by Numbers) If A is a matrix and k is a number, then $k A$ is the matrix having the same dimensions as A, and whose entries are given by

$$(k A)_{ij} = k \cdot A_{ij} \quad\hbox{for all}\quad i, j.$$

(It's considered ugly to write a number on the right side of a matrix if you want to multiply. For the record, I'll define $A k$ to be the same as $k A$ .)

This definition says that to multiply a matrix by a number, multiply each entry by the number.

Definition. If A is a matrix, then $-A$ is the matrix having the same dimensions as A, and whose entries are given by

$$(-A)_{ij} = -A_{ij}.$$

Proposition. Let A and B be matrices with the same dimensions, and let k be a number. Then:

(a) $k(A + B) = k A + k B$ and $k(A - B) = k A - k B$ .

(b) $0 \cdot A = 0$ .

(c) $1 \cdot A = A$ .

(d) $(-1) \cdot A = -A$ .

(e) $A - B = A + (-B)$ .

Note that in (b), the 0 on the left is the number 0, while the 0 on the right is the zero matrix.

Proof. I'll prove (a) and (c) by way of example and leave the proofs of the other parts to you.

First, I want to show that $k(A + B) = k A + k B$ . I have to show that corresponding entries are equal, which means

$$\left(k(A + B)\right)_{ij} = (k A + k B)_{ij}.$$

I apply the definitions of matrix addition and multiplication of a matrix by a number:

$$\left(k(A + B)\right)_{ij} = k \cdot (A + B)_{ij} = k(A_{ij} + B_{ij}) = k A_{ij} + k B_{ij},$$

$$(k A + k B)_{ij} = (k A)_{ij} + (k B)_{ij} = k A_{ij} + k B_{ij}.$$

Therefore, $\left(k(A + B)\right)_{ij} = (k A + k B)_{ij}$ , so $k(A + B) = k A + k B$ .

Next, I want to show that $k(A - B) = k A - k B$ . I just repeat the last proof with "-" in place of "+".

I have to show that corresponding entries are equal, which means

$$\left(k(A - B)\right)_{ij} = (k A - k B)_{ij}.$$

I apply the definitions of matrix subtraction and multiplication of a matrix by a number:

$$\left(k(A - B)\right)_{ij} = k \cdot (A - B)_{ij} = k(A_{ij} - B_{ij}) = k A_{ij} - k B_{ij},$$

$$(k A - k B)_{ij} = (k A)_{ij} - (k B)_{ij} = k A_{ij} - k B_{ij}.$$

Therefore, $\left(k(A - B)\right)_{ij} = (k A - k B)_{ij}$ , so $k(A - B) = k A - k B$ .

For (c), I want to show that $1 \cdot A = A$ . As usual, this means I must show that they have the same $(i, j)^{\rm th}$ entries:

$$(1 \cdot A)_{ij} = A_{ij}.$$

I use the definition of multiplying a matrix by a number:

$$(1 \cdot A)_{ij} = 1 \cdot A_{ij} = A_{ij}.$$

This proves that $1 \cdot A = A$ .

Suppose A and B are matrices with compatible dimensions for multiplication. Where does the $(i, j)^{\rm th}$ entry of $A B$ come from? It comes from multiplying the $i^{\rm th}$ row of A with the $j^{\rm th}$ column of B:

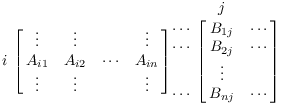
$$\bordermatrix{& & & & \cr & \vdots & \vdots & & \vdots \cr i & A_{i1} & A_{i2} & \cdots & A_{in} \cr & \vdots & \vdots & & \vdots \cr} \bordermatrix{& j & \cr \cdots & B_{1j} & \cdots \cr \cdots & B_{2j} & \cdots \cr & \vdots & \cr \cdots & B_{nj} & \cdots \cr}$$

Corresponding elements are multiplied, and then the products are summed:

$$A_{i1} B_{1j} + A_{i2} B_{2j} + \cdots + A_{in} B_{nj}.$$

Look at the pattern of the subscripts in this sum. You can see that the "inner" matching subscripts are going from 1 to n, while the "outer" "i" and "j" don't change. Hence, I can write the $(i, j)^{\rm th}$ entry of the product in summation form as

$$\sum_{k = 1}^n A_{ik} B_{kj}.$$

That is

$$(A B)_{ij} = \sum_{k = 1}^n A_{ik} B_{kj}.$$

Definition. ( Multiplication) Let A be an $m \times n$ matrix and let B be an $n \times p$ matrix. The product $A B$ is the $m \times p$ matrix whose $(i, j)^{\rm th}$ entry is given by

$$(A B)_{ij} = \sum_{k = 1}^n A_{ik}B_{kj} \quad\hbox{for all}\quad i, j.$$

It's often useful to have a symbol which you can use to compare two quantities i and j --- specifically, a symbol which equals 1 when $i = j$ and equals 0 when $i \ne j$ .

Definition. The Kronecker delta is defined by

$$\delta_{ij} = \cases{ 1 & if $i = j$ \cr 0 & if $i \ne j$ \cr}.$$

For example,

$$\delta_{12} = 0, \quad \delta_{17,17} = 1, \quad \delta_{84} = 0.$$

Lemma. $\displaystyle \sum_{j = 1}^n \delta_{ij} a_j = a_i$ .

Proof. To see what's happening, write out the sum:

$$\sum_{j = 1}^n \delta_{ij} a_j = \delta_{i1} a_1 + \delta_{i2} a_2 + \delta_{i3} a_3 + \cdots + \delta_{in} a_n.$$

By definition, each $\delta$ with unequal subscripts is 0. The only $\delta$ that is not 0 is the one with equal subscripts. Since i is fixed, the $\delta$ that is not 0 is $\delta_{ii}$ , which equals 1. Thus,

$$\delta_{i1} a_1 + \delta_{i2} a_2 + \delta_{i3} a_3 + \cdots + \delta_{ii} a_i + \cdots + \delta_{in} a_n = 0 \cdot a_1 + 0 \cdot a_2 + 0 \cdot a_3 + \cdots + 1 \cdot a_i + \cdots + 0 \cdot a_n = a_i.\quad\halmos$$

Definition. The $n \times n$ identity matrix $I_n$ is the $n \times n$ matrix whose $(i, j)^{\rm th}$ entry is given by

$$I_{ij} = \delta_{ij} \quad\hbox{for all}\quad i, j.$$

I will write I instead of $I_n$ if there's no risk of confusion.

Before I give the next result, I'll discuss a technique which is often used when you have two summations, one inside the other. For example, suppose you have

$$\sum_{i = 1}^2 \sum_{j = 0}^3 (a_i + b_j).$$

If I write out the terms, they look like this:

$$\matrix{ & (a_1 + b_0) + (a_1 + b_1) + (a_1 + b_2) + (a_1 + b_3) + \cr & (a_2 + b_0) + (a_2 + b_1) + (a_2 + b_2) + (a_2 + b_3) \cr}$$

You can see I "cycled" through the inner ("j") index from 0 to 3 first, while holding $i = 1$ . Then I changed i to 2, and cycled through the j index again. To interchange the order of summation means that I will get the same sum if I cycle through i first, then j. That is,

$$\sum_{i = 1}^2 \sum_{j = 0}^3 (a_i + b_j) = \sum_{j = 0}^3 \sum_{i = 1}^2 (a_i + b_j).$$

Here is how $\displaystyle \sum_{j = 0}^3 \sum_{i = 1}^2 (a_i + b_j)$ looks if I write out the terms:

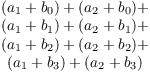
$$\matrix{ & (a_1 + b_0) + (a_2 + b_0) + \cr & (a_1 + b_1) + (a_2 + b_1) + \cr & (a_1 + b_2) + (a_2 + b_2) + \cr & (a_1 + b_3) + (a_2 + b_3) \cr}$$

You can see that I get exactly the same terms, just in a different order. Therefore, the sums are the same.

In general, if $a_{i j}$ is some expression involving i and j, then

$$\sum_{i = 1}^m \sum_{j = 1}^n a_{i j} = \sum_{j = 1}^n \sum_{i = 1}^m a_{i j}.$$

A similar result holds for three or more sums.

I will use interchanging the order of summation in proving associativity of matrix multiplication.

Proposition.

(a) ( Associativity of Matrix Multiplication) If A, B, and C are matrices which are compatible for multiplication, then

$$(A B)C = A(B C).$$

(b) ( Distributivity of Multiplication over Addition) If A, B, C, D, E, and F are matrices compatible for addition and multiplication, then

$$A(B + C) = A B + A C \quad\hbox{and}\quad (D + E)F = D F + E F.$$

(c) If j and k are numbers and A and B are matrices which are compatible for multiplication, then

$$k(A B) = (k A)B = A(k B) \quad\hbox{and}\quad (j k)A = j(k A).$$

(d) ( Identity for Multiplication) If A is an $m \times n$ matrix, then

$$A I_n = A \quad\hbox{and}\quad I_m A = A.$$

The "compatible for addition" and "compatible for multiplication" assumptions mean that the matrices should have dimensions which make the operations in the equations legal --- but otherwise, there are no restrictions on what the dimensions can be.

Proof. I'll prove (a) and part of (d) by way of example, and leave the proofs of the other parts to you.

Before starting, I should say that this proof is rather technical, but try to follow along as best you can. I'll use i, j, k, and l as subscripts.

Suppose that A is an $m \times n$ matrix, B is an $n \times p$ matrix, and C is a $p \times q$ matrix. I want to prove that $(AB)C = A(BC)$ . I have to show that corresponding entries are equal, i.e.

$$\left((A B)C\right)_{il} = \left(A(B C)\right)_{il}.$$

By definition of matrix multiplication,

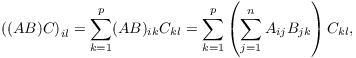
$$\left((A B)C\right)_{il} = \sum_{k = 1}^p (A B)_{ik} C_{kl} = \sum_{k = 1}^p \left(\sum_{j = 1}^n A_{ij} B_{jk}\right) C_{kl},$$

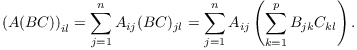
$$\left(A(B C)\right)_{il} = \sum_{j = 1}^n A_{ij} (B C)_{jl} = \sum_{j = 1}^n A_{ij} \left(\sum_{k = 1}^p B_{jk} C_{kl}\right).$$

If you stare at those two terrible double sums for a while, you can see that they involve the same A, B, and C terms, and they involve the same summations --- but in different orders. I'm allowed to convert one into the other by interchanging the order of summation, and using the distributive law:

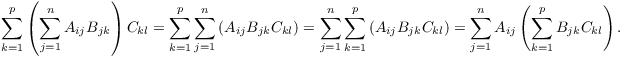
$$\sum_{k = 1}^p \left(\sum_{j = 1}^n A_{ij} B_{jk}\right) C_{kl} = \sum_{k = 1}^p \sum_{j = 1}^n \left(A_{ij} B_{jk} C_{kl}\right) = \sum_{j = 1}^n \sum_{k = 1}^p \left(A_{ij} B_{jk} C_{kl}\right) = \sum_{j = 1}^n A_{ij} \left(\sum_{k = 1}^p B_{jk} C_{kl}\right).$$

Therefore, $\left((A B)C\right)_{il} = \left(A(B C)\right)_{il}$ , and so $(A B)C = A(B C)$ . Wow!

Next, I'll prove the second part of (d), namely that $I_m A = A$ . As usual, I must show that corresponding entries are equal:

$$(I_m A)_{ij} = A_{ij}.$$

By definition of matrix multiplication and the identity matrix,

$$(I_m A)_{ij} = \sum_{k = 1}^m \delta_{ik} A_{kj}.$$

Using the lemma I proved on the Kronecker delta, I get

$$\sum_{k = 1}^m \delta_{ik} A_{kj} = A_{ij}.$$

Thus, $(I_m A)_{ij} = A_{ij}$ , and so $I_m A = A$ .

Definition. Let A be an $m \times n$ matrix. The transpose of A is the $n \times m$ matrix whose $(i, j)^{\rm th}$ entry is given by

$$(A^T)_{ij} = A_{ji} \quad\hbox{for all}\quad i, j.$$

Proposition. Let A and B be matrices of the same dimension, and let k be a number. Then:

(a) $(A^T)^T = A$ .

(b) $(A + B)^T = A^T + B^T$ .

(c) $(k A)^T = k A^T$ .

Proof. I'll prove (b) by way of example and leave the proofs of the other parts for you.

I want to show that $(A + B)^T = A^T + B^T$ . I have to show the corresponding entries are equal:

$$\left((A + B)^T\right)_{ij} = (A^T + B^T)_{ij}.$$

Now

$$\left((A + B)^T\right)_{ij} = (A + B)_{ji} = A_{ji} + B_{ji}.$$

$$(A^T + B^T)_{ij} = (A^T)_{ij} + (B^T)_{ij} = A_{ji} + B_{ji}.$$

Thus, $\left((A + B)^T\right)_{ij} = (A^T + B^T)_{ij}$ , so $(A + B)^T = A^T + B^T$ .

Proposition. Suppose A and B are matrices which are compatible for multiplication. Then

$$(A B)^T = B^T A^T.$$

Proof. I'll derive this using the matrix multiplication formula.

$$(A B)_{ij} = \sum_{k = 1}^n A_{ik} B_{kj}.$$

Let $(A^T)_{ij}$ denote the $(i, j)^{\rm th}$ entry of $A^T$ , and likewise for B and $A B$ . Then

$$[(A B)^T]_{ji} = (A B)_{ij} = \sum_{k = 1}^n A_{ik} B_{kj} = \sum_{k = 1}^n (A^T)_{ki} (B^T)_{jk} = \sum_{k = 1}^n (B^T)_{jk} (A^T)_{ki}.$$

The product on the right is the $(j, i)^{\rm th}$ entry of $B^T A^T$ , while $[(A B)^T]_{ji}$ is the $(j, i)^{\rm th}$ entry of $(A B)^T$ . Therefore, $(A B)^T = B^T A^T$ , since their corresponding entries are equal.

Definition.

(a) A matrix X is symmetric if $X^T = X$ .

(b) A matrix X is skew symmetric if $X^T = -X$ .

Both definitions imply that X is a square matrix.

Using the definition of transpose, I can express these definitions in terms of elements.

X is symmetric if

$$X_{ij} = X_{ji} \quad\hbox{for all}\quad i, j.$$

X is skew symmetric if

$$X_{ij} = -X_{ji} \quad\hbox{for all}\quad i, j.\quad\halmos$$

Visually, a symmetric matrix is symmetric across its main diagonal (the diagonal running from northwest to southeast). For example, this real matrix is symmetric:

$$\left[\matrix{ 0 & 2 & -9 \cr 2 & \sqrt{3} & 4 \cr -9 & 4 & 5 \cr}\right].$$

Here's a skew symmetric real matrix:

$$\left[\matrix{ 0 & -3 & -2 \cr 3 & 0 & 17 \cr 2 & -17 & 0 \cr}\right].$$

Entries which are symmetrically located across the main diagonals are negatives of one another. The entries on the main diagonal must be 0, since they must be equal to their negatives.

The next result is pretty easy, but it illustrates how you can use the definitions of symmetry and skew symmetry in writing proofs. In these proofs, in contrast to earlier proofs, I don't need to write out the entries of the matrices, since I can use properties I've already proved.

Proposition.

(a) The sum of symmetric matrices is symmetric.

(b) The sum of skew symmetric matrices is skew symmetric.

Proof. (a) Let A and B be symmetric. I must show that $A + B$ is symmetric. Now

$$(A + B)^T = A^T + B^T = A + B.$$

The first equality follows from a property I proved for transposes. The second equality follows from the fact that A is symmetric (so $A^T = A$ ) and B is symmetric (so $B^T = B$ ).

Since $(A + B)^T = A + B$ , it follows that $A + B$ is symmetric.

(b) Let A and B be skew symmetric, so $A^T = -A$ and $B^T = -B$ . I must show that $A + B$ is skew symmetric. Now

$$(A + B)^T = A^T + B^T = -A + (-B) = -(A + B).$$

Therefore, $A + B$ is skew symmetric.

Contact information

Bruce Ikenaga's Home Page

Copyright 2020 by Bruce Ikenaga