Commutative Rings and Fields

Different algebraic systems are used in linear algebra. The most important are commutative rings with identity and fields. I'll begin by stating the axioms for a ring. They will look abstract, because they are! But don't worry --- lots of examples will follow.

Definition. A ring is a set R with two binary operations addition (denoted +) and multiplication (denoted $\cdot$ ). These operations satisfy the following axioms:

1. Addition is associative: If $a, b, c \in R$ , then

$$a + (b + c) = (a + b) + c.$$

2. There is an identity for addition, denoted 0. It satisfies

$$0 + a = a \quad\hbox{and}\quad a + 0 = a \quad\hbox{for all} \quad a \in R.$$

3. Every every of R has an additive inverse. That is, if $a \in R$ , there is an element $-a \in R$ which satisfies

$$a + (-a) = 0 \quad\hbox{and}\quad (-a) + a = 0.$$

4. Addition is commutative: If $a, b \in R$ , then

$$a + b = b + a.$$

5. Multiplication is associative: If $a, b, c \in R$ , then

$$a \cdot (b \cdot c) = (a \cdot b) \cdot c.$$

6. Multiplication distributes over addition: If $a, b, c \in R$ , hen

$$a \cdot (b + c) = a\cdot b + a\cdot c.$$

It's common to drop the "$\cdot$ " in "$a \cdot b$ " and just write "$a b$ ". I'll do this except where the "$\cdot$ " is needed for clarity.

As a convenience, we can define subtraction using additive inverses. If R is a ring and $a, b \in R$ , then $a - b$ is defined to be $a + (-b)$ . That is, subtraction is defined as adding the additive inverse.

You might notice that we now have three of the usual four arithmetic operations: Addition, subtraction, and multiplication. We don't necessarily have a "division operation" in a ring; we'll discuss this later.

If you've never seen axioms for a mathematical structure laid out like this, you might wonder: What am I supposed to do? Do I memorize these? Actually, if you look at the axioms, they say things that are "obvious" from your experience. For example, Axiom 4 says addition is commutative. So as an example for real numbers,

$$117 + 33 = 33 + 117.$$

You can see that, as abstract as they look, these axioms are not that big a deal. But when you do mathematics carefully, you have to be precise about what the rules are. You will not have much to do in this course with writing proofs from these axioms, since that belongs in an abstract algebra course. A good rule of thumb might be to try to understand by example what an axiom says. And if it seems "obvious" or "familiar" based on your experience, don't worry about it. Where you should pay special attention is when things don't work in the way you expect.

If you look at the axioms carefully, you might notice that some familiar properties of multiplication are missing. We will single them out next.

Definition. A ring R is commutative if the multiplication is commutative. That is, for all $a, b \in R$ ,

$$a b = b a.$$

Note: The word "commutative" in the phrase "commutative ring" always refers to multiplication --- since addition is always assumed to be commutative, by Axiom 4.

Definition. A ring R is a ring with identity if there is an identity for multiplication. That is, there is an element $1 \in R$ such that

$$1 \cdot a = a \quad\hbox{and}\quad a \cdot 1 = a \quad\hbox{for all}\quad a \in R.$$

Note: The word "identity" in the phrase "ring with identity" always refers to an identity for multiplication --- since there is always an identity for addition (called "0"), by Axiom 2.

A commutative ring which has an identity element is called a commutative ring with identity.

In a ring with identity, you usually also assume that $1 \ne 0$ . (Nothing stated so far requires this, so you have to take it as an axiom.) In fact, you can show that if $1 = 0$ in a ring R, then R consists of 0 alone --- which means that it's not a very interesting ring!

Here are some number systems you're familiar with:

(a) The integers $\integer$ .

(b) The rational numbers $\rational$ .

(c) The real numbers $\real$ .

(d) The complex numbers $\complex$ .

Each of these is a commutative ring with identity. In fact, all of them except $\integer$ are fields. I'll discuss fields below.

By the way, it's conventional to use a capital letter with the vertical or diagonal stroke "doubled" (as in $\integer$ or $\real$ ) to stand for number systems. It is how you would write them by hand. If you're typing them, you usually use a special font; a common one is called Blackboard Bold.

You might wonder why I singled out the commutativity and identity axioms, and didn't just make them part of the definition of a ring. (Actually, many people add the identity axiom to the definition of a ring automatically.) In fact, there are situations in mathematics where you deal with rings which aren't commutative, or (less often) lack an identity element. We'll see, for instance, that matrix multiplication is usually not commutative.

The idea is to write proofs using exactly the properties you need. In that way, the things that you prove can be used in a wider variety of situations. Suppose I had included commutativity of multiplication in the definition of a ring. Then if I proved something about rings, you would not know whether it applied to noncommutative rings without carefully checking the proof to tell whether commutativity was used or not. If you really need a ring to be commutative in order to prove something, it is better to state that assumption explicitly, so everyone knows not to assume your result holds for noncommutative rings.

The next example (or collection of examples) of rings may not be familiar to you. These rings are the integers mod n. For these rings, n will denote an integer. Actually, n can be any integer if I modify the discussion a little, but to keep things simple, I'll take $n \ge 2$ .

The integers mod n is the set

$$\integer_n = \{0, 1, 2, \ldots, n - 1\}.$$

n is called the modulus.

For example,

$$\integer_2 = \{0, 1\} \quad\hbox{and}\quad \integer_6 = \{0, 1, 2, 3, 4, 5\}.$$

$\integer_n$ becomes a commutative ring with identity under the operations of addition mod n and multiplication mod n. I won't prove this; I'll just show you how to work with these operations, which is sufficient for a linear algebra course. You'll see a rigorous treatment of $\integer_n$ in abstract algebra.

(a) To add x and y mod n, add them as integers to get $x + y$ . Then divide $x + y$ by n and take the remainder --- call it r. Then $x + y = r$ .

(b) To multiply x and y mod n, multiply them as integers to get $xy$ . Then divide $xy$ by n and take the remainder --- call it r. Then $x y = r$ .

Since modular arithmetic may be unfamiliar to you, let's do an extended example. Suppose $n = 6$ , so the ring is $\integer_6$ .

$$\matrix{ 4 + 5 & = & 9 & \hbox{(Add them as integers \dots}) \cr & = & 3 & \hbox{(Divide 9 by 6 and take the remainder, which is 3)} \cr}$$

Hence, $4 + 5 = 3$ in $\integer_6$ .

You can picture arithmetic mod 6 this way:

$$\hbox{\epsfysize=1.5in \epsffile{rings-1.eps}}$$

You count around the circle clockwise, but when you get to where "6" would be, you're back to 0. To see how $4 + 5$ works, start at 0. Count 4 numbers clockwise to get to 4, then from there, count 5 numbers clockwise. You'll find yourself at 3.

Here is multiplication:

$$\matrix{2 \cdot 5 & = & 10 & \hbox{(Multiply them as integers \dots}) \cr & = & 4 & \hbox{(Divide 10 by 6 and take the remainder, which is 4)} \cr}$$

Hence, $2 \cdot 5 = 4$ in $\integer_6$ .

You can see that as you do computations, you might in the middle get numbers outside $\{0, 1, 2, 3, 4, 5\}$ . But when you divide by 6 and take the remainder, you'll always wind up with a number in $\{0, 1, 2, 3, 4, 5\}$ .

Try it with a big number:

$$80 = 6 \cdot 13 + 2 = 2.$$

Using our circle picture, if you start at 0 and do 80 steps clockwise around the circle, you'll find yourself at 2. (Maybe you don't have the patience to actually do this!) When we divide by 6 then "discard" the multiples of 6, that is like the fact that you return to 0 on the circle after 6 steps.

Notice that if you start with a number that is divisible by 6, you get a remainder of 0:

$$84 = 6 \cdot 14 + 0 = 0.$$

We see that in doing arithmetic mod 6, multiples of 6 are equal to 0. And in general, in doing arithmetic mod n, multiples of n are equal to 0.

Other arithmetic operations work as you'd expect. For example,

$$\matrix{ 3^4 & = & 81 & \hbox{(Take the power as an integer \dots}) \cr & = & 3 & \hbox{(Divide 81 by 6 and take the remainder, which is 3)} \cr}$$

Hence, $3^4 = 3$ in $\integer_6$ .

Negative numbers in $\integer_6$ are additive inverses. Thus, $-2 = 4$ in $\integer_6$ , because $4 + 2 = 0$ . To deal with negative numbers in general, add a positive multiple of 6 to get a number in the set $\{0, 1, 2, 3, 4, 5\}$ . For example,

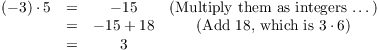
$$\matrix{ (-3) \cdot 5 & = & -15 & \hbox{(Multiply them as integers \dots}) \cr & = & -15 + 18 & \hbox{(Add 18, which is $3 \cdot 6$)} \cr & = & 3 & \cr}$$

Hence, $(-3) \cdot 5 = 3$ in $\integer_6$ .

The reason you can add 18 (or any multiple of 6) is that 18 divided by 6 leaves a remainder of 0. In other words, "$18 = 0$ " in $\integer_6$ , so adding 18 is like adding 0. In a similar way, you can always convert a negative number mod n to a positive number in $\{0, 1, \ldots n - 1\}$ by adding multiples of n. For instance,

$$-14 = -14 + 18 = 4.$$

Remember that multiples of 6 (like 18) are 0 mod 6!

Recall that subtraction is defined as adding the additive inverse. Thus, to do $1 - 2$ in $\integer_6$ , use the fact that the additive inverse of 2 (that is, -2) is equal to 4:

$$1 - 2 = 1 + 4 = 5.$$

We haven't discussed division yet, but maybe the last example tells you how to do it. Just as subtraction is defined as adding the additive inverse, division should be defined as multiplying by the multiplicative inverse. Let's give the definition.

Definition. Let R be a ring with identity, and let $x \in R$ . The multiplicative inverse of x is an element $x^{-1} \in R$ which satisifies

$$x \cdot x^{-1} = 1 \quad\hbox{and}\quad x^{-1} \cdot x = 1.$$

If we were dealing with real numbers, then $3^{-1} = \dfrac{1}{3}$ , for instance. But going back to the $\integer_6$ example, we don't have fractions in $\integer_6$ . So what is (say) $5^{-1}$ in $\integer_6$ ? By definition, $5^{-1}$ is the element (if there is one) in $\integer_6$ which satisfies

$$5 \cdot 5^{-1} = 1.$$

(I could say $5^{-1} \cdot 5 = 1$ , but multiplication is commutative in $\integer_6$ , so the order doesn't matter.)

We just check cases. Remember that if I get a product that is 6 or bigger, I have to reduce mod 6 by dividing and taking the remainder.

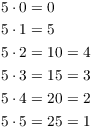
$$\eqalign{ 5 \cdot 0 & = 0 \cr 5 \cdot 1 & = 5 \cr 5 \cdot 2 & = 10 = 4 \cr 5 \cdot 3 & = 15 = 3 \cr 5 \cdot 4 & = 20 = 2 \cr 5 \cdot 5 & = 25 = 1 \cr}$$

I got $25 = 1$ by dividing 25 by the modulus 6 --- it goes in 4 times, with a remainder of 1.

Thus, according to the definition, $5^{-1} = 5$ . In other words, 5 is its own multiplicative inverse. This isn't unheard of: You know that in the real numbers, 1 is its own multiplicative inverse.

This also means that if you want to divide by 5 in $\integer_6$ , you should multiply by 5.

What about $4^{-1}$ in $\integer_6$ ? Unfortunately, if you take cases as I did with 5, you'll see that for every number n in $\integer_6$ , you do not have $4 \cdot n = 1$ . Here's a proof by contradiction which avoids taking cases. Suppose $4 n = 1$ . Multiply both sides by 3:

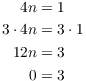
$$\eqalign{ 4 n & = 1 \cr 3 \cdot 4 n & = 3 \cdot 1 \cr 12 n & = 3 \cr 0 & = 3 \cr}$$

I made the last step using the fact that $12 n$ is a multiple of 6 (since $12 = 6 \cdot 2$ ), and multiples of 6 are equal to 0 mod 6. Since "$0 = 3$ " is a contradiction, $4 \cdot n = 1$ is impossible. So $4^{-1}$ is undefined in $\integer_6$ .

It happens to be true that in $\integer_6$ , the elements 0, 2, 3, and 4 do not have multiplicative inverses; 1 and 5 do.

And in $\integer_{10}$ , the elements 0, 2, 4, 5, 6, and 8 do not have multiplicative inverses; 1, 3, 7, and 9 do.

Do you see a pattern?

You probably don't need much practice working with familiar number systems like the real numbers $\real$ , so we'll give some examples which involve arithmetic in $\integer_n$ .

Example. (a) Reduce 22 to a number in $\{0, 1, 2, 3\}$ in $\integer_4$ .

(b) Reduce -21 to a number in $\{0, 1, 2, 3\}$ in $\integer_4$ .

(c) Compute $5 + 11$ in $\integer_{12}$ .

(d) Compute $13 \cdot 5$ in $\integer_{17}$ .

(e) Compute $11 - 14$ in $\integer_{10}$ .

(f) Compute $4^3$ in $\integer_{11}$ .

(g) Compute

$$25! = 1 \cdot 2 \cdot 3 \cdot 4 \cdot \cdots \cdot 25 \quad\hbox{in}\quad \integer_{23}.$$

It's understood for a $\integer_n$ problem your final answer should be a number in $\{0, 1, \ldots n - 1\}$ . You can simplify as you do each step, or simplify at the end (divide by n and take the remainder).

(a) $22 = 4 \cdot 5 + 2 = 2$ .

(b) $-21 = -21 + 24 = 3$ .

Notice that 24 is a multiple of 4, so it's equal to 0 in $\integer_4$ . You can also do this by dividing by 4 if you do it carefully:

$$-21 = 4 \cdot (-6) + 3 = 3.\quad\halmos$$

(c) $5 + 11 = 16 = 12 + 4 = 4$ .

(d) $13 \cdot 5 = 65 = 17 \cdot 3 + 14 = 14$ .

(e) $11 - 14 = -3 = -3 + 20 = 17$ .

Notice that I added a multiple of 10 (since $20 = 10 \cdot 2$ ) to get a positive number.

(f) $4^3 = 64 = 11 \cdot 5 + 9 = 9$ .

(g) $1 \cdot 2 \cdot 3 \cdot 4 \cdot \cdots \cdot 25$ includes all the numbers from 1 to 25; in particular, it includes 23. So the product is a multiple of the modulus 23, and

$$25! = 1 \cdot 2 \cdot 3 \cdot 4 \cdot \cdots \cdot 25 = 0.\quad\halmos$$

Example. (a) Find $7^{-1}$ in $\integer_{10}$ .

(b) Prove that 6 does not have a multiplicative inverse in $\integer_{10}$ .

(a) By trial and error, $7 \cdot 3 = 21 = 20 + 1 = 1$ in $\integer_{10}$ . Therefore, $7^{-1} = 3$ .

(b) Suppose $6 n = 1$ for some n in $\integer_{10}$ . Then

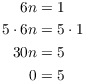
$$\eqalign{ 6 n & = 1 \cr 5 \cdot 6 n & = 5 \cdot 1 \cr 30 n & = 5 \cr 0 & = 5 \cr}$$

The last step follows from the fact that $30 n$ is a multiple of 10, so it equals 0 mod 10. Since "$0 = 5$ " is a contradiction, $6 n = 1$ is impossible, and 6 does not have a multiplicative inverse.

Example. (a) Show that 2 doesn't have a multiplicative inverse in $\integer_4$ .

(b) Show that 14 doesn't have a multiplicative inverse in $\integer_{18}$ .

(a) Try all possibilities:

$$2 \cdot 1 = 2, \quad 2 \cdot 2 = 0, \quad 2 \cdot 3 = 2.$$

There is no element of $\integer_4$ whose product with 2 gives 1. Hence, 2 doesn't have a multiplicative inverse in $\integer_4$ .

(b) Suppose $14 x = 1$ for $x \in \integer_{18}$ . Then

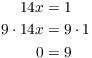
$$\eqalign{ 14 x & = 1 \cr 9 \cdot 14 x & = 9 \cdot 1 \cr 0 & = 9 \cr}$$

(Note that $9 \cdot 14 = 136 = 7 \cdot 18 = 0$ in $\integer_{18}$ .) The last line above is a contradiction, so 14 does not have a multiplicative inverse in $\integer_{18}$ .

You may have noticed that the elements in $\integer_n$ which have multiplicative inverses are the elements which are relatively prime to n.

You might wonder whether there is a systematic way to find multiplicative inverses in $\integer_n$ . The best way is to use the Extended Euclidean Algorithm; you might see it if you take a course in abstract algebra. In this course, I'll usually keep the examples small enough that trial and error is okay for finding multiplicative inverses when you need them. But here's an approach that you might prefer. Suppose you want to find $7^{-1}$ in $\integer_{11}$ . Consider multiples of 11, plus 1. Stop with the first such number that's divisible by 7:

$$\matrix{ 11 + 1 = 12 & (\hbox{Not divisible by 7}) \cr 22 + 1 = 23 & (\hbox{Not divisible by 7}) \cr 33 + 1 = 34 & (\hbox{Not divisible by 7}) \cr 44 + 1 = 45 & (\hbox{Not divisible by 7}) \cr 55 + 1 = 56 & (\hbox{$56 = 7 \cdot 8$}) \cr}$$

From this, I get $7^{-1} = 8$ , because

$$7 \cdot 8 = 56 = 55 + 1 = 11 \cdot 5 + 1 = 1.$$

Example. Find $8^{-1}$ in $\integer_{13}$ .

In $\integer_{13}$ , I have $8 \cdot 5 = 1$ , so $8^{-1} = 5$ . You could do this by trial and error, since $\integer_{13}$ isn't that big:

$$8 \cdot 1 = 8, \quad 8 \cdot 2 = 16 = 3, \quad 8 \cdot 3 = 24 = 11, \quad 8 \cdot 4 = 32 = 6, \quad 8 \cdot 5 = 40 = 1.$$

Alternatively, take multiples of 13 and add 1, stopping when you get a number divisible by 8:

$$\eqalign{ 13 \cdot 1 + 1 & = 14 \quad\hbox{Not divisible by 8}\quad \cr 13 \cdot 2 + 1 & = 27 \quad\hbox{Not divisible by 8}\quad \cr 13 \cdot 3 + 1 & = 40 \quad\hbox{Divisible by 8}\quad \cr}$$

Then $\dfrac{40}{8} = 5$ , so $8^{-1} = 5$ .

Even this approach is too tedious to use with large numbers. The systematic way to find inverses is to use the Extended Euclidean Algorithm.

We saw that in a commutative ring with identity, an element x might not have multiplicative inverse $x^{-1}$ . That in turn would prevent you from "dividing" by x. From the point of view of linear algebra, this is inconvenient. Hence, we single out rings which are "nice" in that every nonzero element has a multiplicative inverse.

Definition. A field F is a commutative ring with identity in which $1 \ne 0$ and every nonzero element has a multiplicative inverse.

By convention, you don't write "$\dfrac{1}{x}$ " instead of "$x^{-1}$ " unless the ring happens to be a ring with "real" fractions (like $\rational$ , $\real$ , or $\complex$ ). You don't write fractions in (say) $\integer_7$ .

If an element x has a multiplicative inverse, you can divide by x by multiplying by $x^{-1}$ . Thus, in a field, you can divide by any nonzero element. (You'll learn in abstract algebra why it doesn't make sense to divide by 0.)

The rationals $\rational$ , the reals $\real$ , and the complex numbers $\complex$ are fields. Many of the examples will use these number systems.

The ring of integers $\integer$ is not a field. For example, 2 is a nonzero integer, but it does not have a multiplicative inverse which is an integer. ($\dfrac{1}{2}$ is not an integer --- it's a rational number.)

$\rational$ , $\real$ , and $\complex$ are all infinite fields --- that is, they all have infinitely many elements. But (for example) $\integer_5$ is a field.

For applications, it's important to consider finite fields like $\integer_5$ . Before I give some examples, I need some definitions.

Definition. Let R be a commutative ring with identity. The characteristic of R is the smallest positive integer n such that $n \cdot 1 = 0$ .

Notation: $\char R = n$ .

If there is no positive integer n such that $n\cdot 1 = 0$ , then $\char R = 0$ .

In fact, if $\char R = n$ , then $n \cdot x = 0$ for all $x \in R$ .

$\integer$ , $\rational$ , $\real$ , and $\complex$ are all rings of characteristic 0. On the other hand, $\char \integer_n = n$ .

Definition. An integer $n > 1$ is prime if its only positive divisors are 1 and n.

The first few prime numbers are

$$2, \quad 3, \quad, 5, \quad 7, \quad 11, \ldots.$$

An integer $n > 1$ which is not prime is composite. The first few composite numbers are

$$4, \quad 6, \quad 8, \quad 9, \ldots.$$

The following important results are proved in abstract algebra courses.

Theorem. The characteristic of a field is either 0 or a prime number.

Theorem. If p is prime and n is a positive integer, there is a field of characteristic p having $p^n$ elements. This field is unique up to ring isomorphism, and is denoted $GF(p^n)$ (the Galois field of order $p^n$ ).

The only unfamiliar thing in the last result is the phrase "ring isomorphism". This is another concept whose precise definition you'll see in abstract algebra. The statement means, roughly, that any two fields with $p^n$ elements are "the same", in that you can get one from the other by just renaming or reordering the elements.

Since the characteristic of $\integer_n$ is n, the first theorem implies the following result:

Corollary. $\integer_n$ is a field if and only if n is prime.

The Corollary tells us that $\integer_2$ , $\integer_{13}$ , and $\integer_{61}$ are fields, since 2, 3, and 61 are prime.

On the other hand, $\integer_6$ is not a field, since 6 isn't prime (because $6 = 2\cdot 3$ ). In fact, we saw it directly when we showed that 4 does not have a multiplicative inverse in $\integer_6$ . Note that $\integer_6$ is a commutative ring with identity.

For simplicity, the fields of prime characteristic that I use in this course will almost always be finite. But what would an infinite field of prime characteristic look like?

As an example, start with $\integer_2 = \{0, 1\}$ . Form the field of rational functions $\integer_2(x)$ . Thus, elements of $\integer_2(x)$ have the form $\dfrac{p(x)}{q(x)}$ where $p(x)$ and $q(x)$ are polynomials with coefficients in $\integer_2$ . Here are some examples of elements of $\integer_2(x)$ :

$$\dfrac{1}{x}, \quad \dfrac{x^2 + x + 1}{x^{100} + 1}, \quad 1, \quad x^7 + x^3 + 1.$$

You can find multiplicative inverses of nonzero elements by taking reciprocals; for instance,

$$\left(\dfrac{x^2 + x + 1}{x^{100} + 1}\right)^{-1} = \dfrac{x^{100} + 1}{x^2 + x + 1}.$$

I won't go through and check all the axioms, but in fact, $\integer_2(x)$ is a field. Moreover, since $2 \cdot 1 = 0$ in $\integer_2(x)$ , it's a field of characteristic 2. It has an infinite number of elements; for example, it contains

$$1, \quad x, \quad x^2, \quad x^3, \quad \ldots.$$

What about fields of characteristic p other than $\integer_2$ , $\integer_3$ , and so on? As noted above, these are called Galois fields. For instance, there is a Galois field with $5^3 = 125$ elements. To keep the computations simple, we will rarely use them in this course. But here's an example of a Galois field with $2^2 = 4$ elements, so you can see what it looks like.

$GF(4)$ is the Galois field with 4 elements, and here are its addition and multiplication tables:

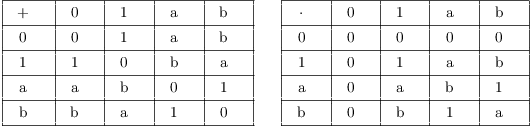
$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr & + & & 0 & & 1 & & a & & b & \cr height2pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr & 0 & & 0 & & 1 & & a & & b & \cr height2pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr & 1 & & 1 & & 0 & & b & & a & \cr height2pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr & a & & a & & b & & 0 & & 1 & \cr height2pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr & b & & b & & a & & 1 & & 0 & \cr height2pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} }} \hskip0.25in \vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr & $\cdot$ & & 0 & & 1 & & a & & b & \cr height2pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr & 0 & & 0 & & 0 & & 0 & & 0 & \cr height2pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr & 1 & & 0 & & 1 & & a & & b & \cr height2pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr & a & & 0 & & a & & b & & 1 & \cr height2pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr & b & & 0 & & b & & 1 & & a & \cr height2pt & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} }} $$

Notice that

$$1 + 1 = 0, \quad a + a = 0, \quad b + b = 0.$$

You can check by examining the multiplication table that multiplication is commutative, that 1 is the multiplicative identity, and that the nonzero elements (1, a, and b) all have multiplicative inverses. For instance, $a^{-1} = b$ , because $a \cdot b = 1$ .

Since we've already seen a lot of weird things with these new number systems, we might as well see another one.

Example. Find the roots of $x^2 + 5 x + 6$ in $\integer_{10}$ .

Make a table:

$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & x & & 0 & & 1 & & 2 & & 3 & & 4 & & 5 & & 6 & & 7 & & 8 & & 9 & \cr height2pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr & $x^2 + 5 x + 6$ & & 6 & & 2 & & 0 & & 0 & & 2 & & 6 & & 2 & & 0 & & 0 & & 2 & \cr height2pt & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} }} $$

For instance, plugging $x = 4$ into $x^2 + 5 x + 6$ gives

$$4^2 + 5 \cdot 4 + 6 = 42 = 40 + 2 = 2.$$

The roots are $x = 2$ , $x = 3$ , $x = 7$ and $x = 8$ .

You would normally not expect a quadratic to have 4 roots! This shows that algebraic facts you may know for real numbers may not hold in arbitrary rings (note that $\integer_{10}$ is not a field).

Linear algebra deals with structures based on fields, and you've now seen most of the fields that will come up in the examples. The modular arithmetic involved in working with $\integer_n$ may be new to you, but it's not that hard with a little practice. And as I noted, most of the examples involving finite fields will use $\integer_p$ for p prime, rather than the more general Galois fields, or infinite fields of characteristic p.

Contact information

Bruce Ikenaga's Home Page

Copyright 2020 by Bruce Ikenaga