The Row Space of a Matrix

We will look at 3 subspaces associated to a matrix: The row space, the column space, and the null space. They provide important information about the matrix and the linear transformation associated to it. In this section, we'll discuss the row space of a matrix. We'll also discuss algorithms for finding a basis for a subspace spanned by a set of vectors, determining whether a set of vectors is independent, and adding vectors to an independent set to get a basis.

A lot of what follows generalizes to matrices with entries in a commutative ring with identity, but we will almost always stick to matrices over a field in this section.

Definition. Let A be an $m \times n$ matrix with entries in a field F. The row vectors of A are the vectors in $F^n$ corresponding to the rows of A. The row space of A is the subspace of $F^n$ spanned by the row vectors of A.

For example, consider the real matrix

$$A = \left[\matrix{1 & 0 \cr 0 & 1 \cr 0 & 0 \cr}\right].$$

The row vectors are $(1, 0)$ , $(0, 1)$ , and $(0, 0)$ . The row space is the subspace of $\real^2$ spanned by these vectors. Since the first two vectors are the standard basis vectors for $\real^2$ , the row space is $\real^2$ .

Lemma. Let A be a matrix with entries in a field. If E is an elementary row operation, then $E(A)$ has the same row space as A.

Proof. If E is an operation of the form $r_i \leftrightarrow r_j$ , then $E(A)$ and A have the same rows (except for order), so it's clear that their row vectors have the same span. Hence, the matrices have the same row space.

If E is an operation of the form $r_i \rightarrow a r_i$ where $a \ne 0$ , then A and $E(A)$ agree except in the i-th row. We have

$$a_1 r_1 + \cdots + a_i r_i + \cdots + a_m r_m = a_1 r_1 + \cdots + \left(a_i a^{-1}\right) (a r_i) + \cdots + a_m r_m,$$

Note that the vectors $r_1$ , ..., $a r_i$ , ..., $r_m$ are the rows of $E(A)$ . So this equation says any linear combination of the rows $r_1$ , ..., $r_m$ of A is a linear combination of the rows of $E(A)$ . This means that the row space of A is contained in the row space of $E(A)$ .

Going the other way, a linear combination of the rows $r_1$ , ..., $a r_i$ , ..., $r_m$ of $E(A)$ looks like this:

$$b_1 r_1 + \cdots + b_i (a r_i) + \cdots + b_m r_m.$$

But this is a linear combination of the rows $r_1$ , ..., $r_m$ of A, so the row space of $E(A)$ is contained in the row space of A. Hence, A and $E(A)$ have the same row space.

Finally, suppose E is a row operation of the form $r_i \rightarrow r_i + a r_j$ , where $a \in F$ . Then

$$a_1 r_1 + \cdots + a_i r_i + \cdots + a_m r_m = a_1 r_1 + \cdots + a_i(r_i + a r_j) + \cdots + (a_j - a_i a)r_j + \cdots + a_m r_m.$$

This shows that the row space of A is contained in the row space of $E(A)$ .

Conversely,

$$a_1 r_1 + \cdots + a_i (r_i + a r_j) + \cdots + a_j r_j + \cdots + a_m r_m = a_1 r_1 + \cdots + a_i r_i + \cdots + (a_i a + a_j)r_j + \cdots + a_m r_m.$$

Hence, the row space of $E(A)$ is contained in the row space of A.

Definition. Two matrices over a field are row equivalent if one can be obtained from the other via elementary row operations.

Since row operations preserve row space, row equivalent matrices have the same row space. In particular, a matrix and its row reduced echelon form have the same row space.

The next proposition describes some of the components of a vector in the row space of a row-reduced echelon matrix R. Such a vector is a linear combination of the nonzero rows of R.

Proposition. Let $R = \{r_{i j}\}$ be a row reduced echelon matrix over a field with nonzero rows $r_1$ , ..., $r_p$ . Suppose the leading entries of R occur at

$$(1,j_1),\ (2, j_2), \ldots, \quad \hbox{where} \quad j_1 < j_2 < \cdots.$$

Suppose $v = (v_1, \ldots, v_n)$ and

$$v = a_1 r_1 + \cdots + a_p r_p.$$

Then $v_{j_k} = a_k$ for all k.

Proof.

$$v_{j_k} = \sum_{i=1}^p a_i r_{i j_k}.$$

But the only nonzero element in column $j_k$ is the leading entry $r_{k j_k} = 1$ . Therefore, the only nonzero term in the sum is $a_k r_{k j_k} = a_k$ .

This result looks a bit technical, but it becomes obvious if you consider an example. Here's a row reduced echelon matrix over $\real$ :

$$\left[\matrix{ 0 & 1 & 2 & 0 & -1 & 0 \cr 0 & 0 & 0 & 1 & 2 & 0 \cr 0 & 0 & 0 & 0 & 0 & 1 \cr 0 & 0 & 0 & 0 & 0 & 0 \cr}\right].$$

Here's a vector in the row space, a linear combination of the nonzero rows:

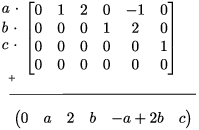
$$\hbox{\epsfysize=1.15in \epsffile{row-space-1.eps}}$$

The leading entries occur in columns $j_1 = 2$ , $j_2 = 4$ , and $j_3 = 6$ . The $2^{\rm nd}$ , $4^{\rm th}$ , and $6^{\rm th}$ components of the vector are

$$v_2 = a, \quad v_4 = b, \quad v_6 = c.$$

You can see from the picture why this happens. The coefficients a, b, c multiply the leading entries. The leading entries are all 1's, and they're the only nonzero elements in their columns. So in the components of the vector corresponding to those columns, you get a, b, and c.

Corollary. The nonzero rows of a row reduced echelon matrix over a field are independent.

Proof. Suppose R is a row reduced echelon matrix with nonzero rows $r_1$ , ..., $r_p$ . Suppose the leading entries of R occur at $(1,j_1), (2, j_2), \ldots$ , where $j_1 < j_2 < \cdots$ . Suppose

$$0 = a_1 r_1 + \cdots + a_p r_p.$$

The proposition implies that $a_k = v_{j_k} = 0$ for all k. Therefore, $\{r_i\}$ are independent.

Corollary. The nonzero rows of a row reduced echelon matrix over a field form a basis for the row space of the matrix.

Proof. The nonzero rows span the row space, and are independent, by the preceding corollary.

Algorithm. Let V be a finite-dimensional vector space, and let $v_1, \ldots, v_m$ be vectors in V. Find a basis for $W = \langle v_1, \ldots, v_m \rangle$ , the subspace spanned by the $v_i$ .

Let M be the matrix whose i-th row is $v_i$ . The row space of M is W. Let R be a row-reduced echelon matrix which is row equivalent to M. Then R and M have the same row space W, and the nonzero rows of R form a basis for W.

Example. Consider the vectors $v_1 = (1, 0, 1, 1)$ , $v_2 = (-2, 1, 1, 0)$ , and $v_3 = (7, -2, 1, 3)$ in $\real^4$ . Find a basis for the subspace $\langle v_1, v_2, v_3 \rangle$ spanned by the vectors.

Construct a matrix with the $v_i$ as its rows and row reduce:

$$\left[\matrix{ 1 & 0 & 1 & 1 \cr -2 & 1 & 1 & 0 \cr 7 & -2 & 1 & 3 \cr}\right] \quad \to \quad \left[\matrix{ 1 & 0 & 1 & 1 \cr 0 & 1 & 3 & 2 \cr 0 & 0 & 0 & 0 \cr}\right]$$

The vectors $(1, 0, 1, 1)$ and $(0, 1, 3, 2)$ form a basis for $\langle v_1, v_2, v_3 \rangle$ .

Example. Determine the dimension of the subspace of $\real^3$ spanned by $(1, 2, -1)$ , $(1, 1, 1)$ , and $(2, -2, 1)$ .

Form a matrix using the vectors as the rows and row reduce:

$$\left[\matrix{ 1 & 2 & -1 \cr 1 & 1 & 1 \cr 2 & -2 & 1 \cr}\right] \quad \to \quad \left[\matrix{ 1 & 0 & 0 \cr 0 & 1 & 0 \cr 0 & 0 & 1 \cr}\right]$$

The subspace has dimension 3, since the row reduced echelon matrix has 3 nonzero rows.

Definition. The rank of a matrix over a field is the dimension of its row space.

Example. Find the rank of the following matrix over $\integer_5$ :

$$\left[\matrix{ 1 & 4 & 2 & 1 \cr 3 & 3 & 1 & 2 \cr 0 & 1 & 0 & 4 \cr}\right].$$

Row reduce the matrix:

$$\left[\matrix{ 1 & 4 & 2 & 1 \cr 3 & 3 & 1 & 2 \cr 0 & 1 & 0 & 4 \cr}\right] \quad \to \quad \left[\matrix{ 1 & 0 & 2 & 0 \cr 0 & 1 & 0 & 4 \cr 0 & 0 & 0 & 0 \cr}\right]$$

The row reduced echelon matrix has 2 nonzero rows. Therefore, the original matrix has rank 2.

I'll need the following fact about matrix multiplication for the proof of the next lemma. Consider the following multiplication:

$$\left[\matrix{a_1 & a_2 & \cdots & a_n \cr}\right] \left[\matrix{\leftarrow & r_1 & \rightarrow \cr \leftarrow & r_2 & \rightarrow \cr & \vdots & \cr \leftarrow & r_n & \rightarrow \cr}\right].$$

In doing the multiplication, each $a_i$ multiplies the corresponding row $r_i$ . The result is a linear combination of the $r_i$ 's with the $a_i$ 's as coefficients. Here's the picture:

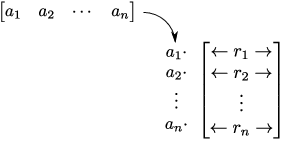
$$\hbox{\epsfysize=1.25in \epsffile{row-space-2.eps}}$$

Therefore,

$$\left[\matrix{ a_1 & a_2 & \cdots & a_n \cr}\right] \left[\matrix{\leftarrow & r_1 & \rightarrow \cr \leftarrow & r_2 & \rightarrow \cr & \vdots & \cr \leftarrow & r_n & \rightarrow \cr}\right] = \left[\matrix{a_1 r_1 + a_2 r_2 + \cdots + a_n r_n \cr}\right].$$

If instead of a single row vector on the left I have an entire matrix, here's what I get:

$$\left[\matrix{ a_{1 1} & a_{1 2} & \cdots & a_{1 n} \cr a_{2 1} & a_{2 2} & \cdots & a_{2 n} \cr \vdots & \vdots & & \vdots \cr a_{m 1} & a_{m 2} & \cdots & a_{mn } \cr}\right] \left[\matrix{ \leftarrow & r_1 & \rightarrow \cr \leftarrow & r_2 & \rightarrow \cr & \vdots & \cr \leftarrow & r_n & \rightarrow \cr}\right] = \left[\matrix{ \leftarrow & a_{1 1} r_1 + a_{1 2} r_2 + \cdots + a_{1 n} r_n & \rightarrow \cr \leftarrow & a_{2 1} r_1 + a_{2 2} r_2 + \cdots + a_{2 n} r_n & \rightarrow \cr & \vdots & \cr \leftarrow & a_{m 1} r_1 + a_{m 2} r_2 + \cdots + a_{m n} r_n & \rightarrow \cr}\right].$$

Hence, the rows of the product are linear combinations of the rows $r_1$ , $r_2$ , ... $r_n$ .

Proposition. Let M and N be matrices over a field F which are compatible for multiplication. Then

$$\rank (M N) \le \rank N.$$

Proof. The preceding discussion shows that the rows of $M N$ are linear combinations of the rows of N. Therefore, the rows of $M N$ are all contained in the row space of N.

The row space of N is a subspace, so it's closed under taking linear combinations of vectors. Hence, any linear combination of the rows of $M N$ is in the row space of N. Therefore, the row space of $M N$ is contained in the row space of N.

From this, it follows that the dimension of the row space of $M N$ is less than or equal to the dimension of the row space of N --- that is, $\rank (M N) \le \rank N$ .

I already have one algorithm for testing whether a set of vectors in $F^n$ is independent. That algorithm involves constructing a matrix with the vectors as the columns, then row reducing. The algorithm will also produce a linear combination of the vectors which adds up to the zero vector if the set is dependent.

If all you care about is whether or not a set of vectors in $F^n$ is independent --- i.e. you don't care about a possible dependence relation --- the results on rank can be used to give an alternative algorithm. In this approach, you construct a matrix with the given vectors as the rows.

Algorithm. Let V be a finite-dimensional vector space, and let $v_1, \ldots, v_m$ be vectors in V. Determine whether the set $\{v_1, \ldots, v_m\}$ is independent.

Let M be the matrix whose i-th row is $v_i$ . Let R be a row reduced echelon matrix which is row equivalent to M. If R has m nonzero rows, then $\{v_1, \ldots, v_m\}$ is independent. Otherwise, the set is dependent.

If R has p nonzero rows, then R and M have rank p. (They have the same rank, because they have the same row space.) Suppose $p = m$ . Since $\{v_i\}$ spans, some subset of $\{v_i\}$ is a basis. However, a basis must contain $p = m$ elements. Therefore, $\{v_i\}$ must be independent.

Any independent subset of the row space must contain $\le p$ elements. Hence, if $m > p$ , $\{v_i\}$ must be dependent.

Example. Determine whether the vectors $v_1 = (1, 0, 1, 1)$ , $v_2 = (-2, 1, 1, 0)$ , and $v_3 = (7, -2, 1, 3)$ in $\real^4$ are independent.

Form a matrix with the vectors as the rows and row reduce:

$$\left[\matrix{ 1 & 0 & 1 & 1 \cr -2 & 1 & 1 & 0 \cr 7 & -2 & 1 & 3 \cr}\right] \quad \to \quad \left[\matrix{ 1 & 0 & 1 & 1 \cr 0 & 1 & 3 & 2 \cr 0 & 0 & 0 & 0 \cr}\right]$$

The row reduced echelon matrix has only two nonzero rows. Hence, the vectors are dependent.

I already know that every matrix can be row reduced to a row reduced echelon matrix. The next result completes the discussion by showing that the row reduced echelon form is unique

Proposition. Every matrix over a field can be row reduced to a unique row reduced echelon matrix.

Proof. Suppose M row reduces to R, a row reduced echelon matrix with nonzero rows $r_1, \ldots, r_p$ . Suppose the leading coefficients of R occur at $(1, j_1), (2, j_2), \ldots $ , where $j_1 < j_2 < \cdots $ .

Let W be the row space of R and let $v = (v_1, \ldots, v_n) \ W$ . Since $r_1$ , ... $r_p$ span the row space W, we have

$$v = a_1 r_1 + \cdots + a_p r_p.$$

Claim: The first nonzero component of v must occur in column $j_k$ , for some $k = 1, 2, \ldots$ .

Suppose $a_k$ is the first $a_i$ which is nonzero. Since the $a_i r_i$ terms before $a_k r_k$ are zero, we have

$$v = a_k r_k + \cdots + a_p r_p.$$

The first nonzero element of $r_k$ is a 1 at $(k, j_k)$ . The first nonzero element in $r_{k + 1}, \ldots, r_p$ lies to the right of column $j_k$ . Thus, $v_j = 0$ for $j < j_k$ , and $v_{j_k} = a_k$ . Evidently, this is the first nonzero component of v. This proves the claim.

This establishes that if a row reduced echelon matrix $R'$ is row equivalent to M, its leading coefficients must lie in the same columns as those of R. For the rows of $R'$ are elements of W, and the claim applies.

Next, I'll show that the nonzero rows of $R'$ are the same as the nonzero row of R.

Consider, for instance, the first nonzero rows of R and $R'$ . Their first nonzero components are 1's lying in column $j_1$ . Moreover, both $r_1$ and $r_1'$ have zeros in columns $j_2$ , $j_3$ , ... .

Suppose $r_1 \ne r_1'$ . Then $r_1 - r_1'$ is a nonzero vector in W whose first nonzero component is not in column $j_1$ , $j_2$ , ..., which is a contradiction.

The same argument applies to show that $r_k = r_k'$ for all k. Therefore, $R = R'$ .

In my discussion of bases, I showed that every independent set is a subset of a basis. To put it another way, you can add vectors to an independent set to get a basis.

$$\hbox{\epsfysize=2in \epsffile{row-space-3.eps}}$$

Here's how to find specific vectors to add to an independent set to get a basis.

Example. The following set of vectors in $\real^5$ is independent:

$$\left\{(2, -4, 1, 0, 8),\ (-1, 2, -1, -1, -4),\ (2, -4, 1, 1, 7)\right\}$$

Add vectors to the set to make a basis for $\real^5$ .

If I make a matrix with these vectors as rows and row reduce, the row reduced echelon form will have the same row space (i.e. the same span) as the original set of vectors:

$$\left[\matrix{ 2 & -4 & 1 & 0 & 8 \cr -1 & 2 & -1 & -1 & -4 \cr 2 & -4 & 1 & 1 & 7 \cr}\right] \quad \to \quad \left[\matrix{ 1 & -2 & 0 & 0 & 3 \cr 0 & 0 & 1 & 0 & 2 \cr 0 & 0 & 0 & 1 & -1 \cr}\right]$$

Since there are three nonzero rows and the original set had three vectors, the original set of vectors is indeed independent.

By examining the row reduced echelon form, I see that the vectors $(0, 1, 0, 0, 0)$ and $(0, 0, 0, 0, 1)$ will not be linear combinations of the others. Reason: A nonzero linear combination of the rows of the row reduced echelon form must have a nonzero entry in at least one of the first, third, or fourth columns, since those are the columns containing the leading entries.

In other words, I'm choosing standard basis vectors with a 1's in positions not occupied by leading entries in the row reduced echelon form. Therefore, I can add $(0, 1, 0, 0, 0)$ and $(0, 0, 0, 0, 1)$ to the set and get a new independent set:

$$\left\{(2, -4, 1, 0, 8),\ (-1, 2, -1, -1, -4),\ (2, -4, 1, 1, 7), (0, 1, 0, 0, 0),\ (0, 0, 0, 0, 1)\right\}.$$

There are 5 vectors in this set, so it is a basis for $\real^5$ .

Contact information

Bruce Ikenaga's Home Page

Copyright 2023 by Bruce Ikenaga