I'll review some basics about sets and some of the number systems we'll use. If you're familiar with these things, you can skim this section and refer to it later when you need to.
A set is informally described as a collection of objects. The objects are elements of the set, or members of the set. So a set is kind of like a bag, and its elements are things in the bag.
However, it's easy to get into trouble with that informal description. Trouble can be fun, so let's see how you can get into trouble here. Russell's paradox is named after the British mathematician Bertrand Russell. Here's how it goes. Suppose X is the set whose members are sets which are not members of themselves. (Thus, X is a bag, and the members of X --- the things in the bag --- are themselves bags.) Now is X a member of X? It either is or it isn't.
If X is a member of X, then X is a set which is not a member of itself, by the definition of X. So X is both a member of itself and not a member of itself.
If X is not a member of X, then X is a set which is not a member of itself, so it should be a member of X, by definition of X. Again, X is both a member of itself and not a member of itself.
You may have to think about this a bit, since the words can make your eyes glaze over!
You can see that both alternatives lead to a contradiction. Something is wrong, and it lies in the way we created the set X. It turns out that, to deal with sets in a rigorous way, you have to be careful about how sets can be created. The Zermelo-Fraenkel-Choice Axioms do this, and they are one of the most commonly accepted foundations for mathematics. If you're interested in learning more, you should take a course or read a book in set theory or mathematical logic.
We will stay out of trouble by avoiding weird sets like the one in Russell's paradox.
Let's start by reviewing common set constructions and notations. If A and B are sets, then:
(a) ![]() means that x is an element or
member of A. Likewise,
means that x is an element or
member of A. Likewise, ![]() means that
means that
![]() and
and ![]() are elements of X.
are elements of X.
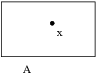
We'll often use schematic diagrams like this one (sometimes called Venn diagrams) to picture arbitrary sets. The sets are drawn as rectangles or ovals or other closed shapes, and you think of the elements of the sets as being stuff inside. In this case, the dot labelled "x" is a particular element of A.
(b) A and B are equal if they have exactly the
same elements. In that case, we write ![]() .
.
(c) ![]() means that A is a subset of B
--- that is, every element of A is also an element of B. It is
possible in this case that
means that A is a subset of B
--- that is, every element of A is also an element of B. It is
possible in this case that ![]() ; if we don't want to allow
; if we don't want to allow ![]() ,
we'll write
,
we'll write ![]() and say that A is a
proper subset of B.
and say that A is a
proper subset of B.

(d) ![]() is the intersection of A and B
--- that is, all the elements which A and B have in common.
is the intersection of A and B
--- that is, all the elements which A and B have in common.

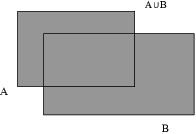
(e) ![]() is the union of A and B ---
that is, all the elements which are in A or are in B (or are in
both).
is the union of A and B ---
that is, all the elements which are in A or are in B (or are in
both).
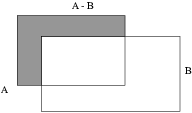
(f) ![]() is the complement of B
relative to A --- that is, all the elements of A which are not
elements of B.
is the complement of B
relative to A --- that is, all the elements of A which are not
elements of B.
If there is some "big set" S and everything under
discussion is contained in S, you can denote the complement of a set
A relative to S (sometimes called the absolute
complement) by ![]() . In order words,
. In order words, ![]() is short for
is short for ![]() when the "big set" S is
understood.
when the "big set" S is
understood.

(g) The empty set is the set with no elements.
It is denoted ![]() or
or ![]() . (But
"
. (But
"![]() " is not the empty set --- if the empty
set is like an empty bag, then "
" is not the empty set --- if the empty
set is like an empty bag, then "![]() " is
like a bag containing an empty bag.)
" is
like a bag containing an empty bag.)
(h) If S and T are sets, their (Cartesian)
product consists of all ordered pairs
![]() , where
, where ![]() and
and ![]() . "Ordered"
means, for example, that
. "Ordered"
means, for example, that ![]() and
and ![]() are different
ordered pairs.
are different
ordered pairs.
For example, if ![]() and
and ![]() , then
, then
![]()
Likewise, ![]() consists of ordered triples
consists of ordered triples ![]() , where
, where ![]() ,
, ![]() , and
, and ![]() .
.
We'll sometimes abbreviate ![]() to
to ![]() , and so on.
, and so on.
The sets which make up standard number systems have special symbols.
(a) ![]() is the set of integers (positive, negative, and 0).
is the set of integers (positive, negative, and 0).
(b) ![]() is the set of rational numbers, which can be
represented as quotients of integers. (Thus,
is the set of rational numbers, which can be
represented as quotients of integers. (Thus, ![]() includes
includes ![]() , since (for instance)
, since (for instance) ![]() .) The use of the letter
"Q" is apparently due to the Italian mathematician Giuseppe
Peano and stands for the Italian word for "quotient".
.) The use of the letter
"Q" is apparently due to the Italian mathematician Giuseppe
Peano and stands for the Italian word for "quotient".
(c) ![]() is the set of real numbers, which are often
represented as decimals (finite or infinite).
is the set of real numbers, which are often
represented as decimals (finite or infinite). ![]() includes
includes ![]() (and so it includes
(and so it includes ![]() ).
).
(d) ![]() is the set of complex numbers: Numbers that can be
written in the form
is the set of complex numbers: Numbers that can be
written in the form ![]() , where a and b are real numbers and
, where a and b are real numbers and ![]() . The old phrase "imaginary numbers" is not
that good --- there's nothing "imaginary" about
. The old phrase "imaginary numbers" is not
that good --- there's nothing "imaginary" about ![]() ! --- and so is less often used.
! --- and so is less often used. ![]() includes
includes ![]() ---
for instance, the real number 13 can be written as
---
for instance, the real number 13 can be written as ![]() --- so
--- so ![]() also includes
also includes ![]() and
and ![]() . Using our subset notation, we could write
. Using our subset notation, we could write ![]() , for instance.
, for instance.
The convention is to use boldface capital letters (like " Z" or " Q")
or "blackboard bold" capital letters (like ![]() ,
, ![]() ,
, ![]() ,
, ![]() ) for "number systems".
You may see other letters (like the quaternions
) for "number systems".
You may see other letters (like the quaternions ![]() ) used as
well. I'll use blackboard bold, since it is easier to distinguish
blackboard bold letters from ordinary capital letters than boldface.
It's also the way you write these symbols on blackboards or in
handwriting.
) used as
well. I'll use blackboard bold, since it is easier to distinguish
blackboard bold letters from ordinary capital letters than boldface.
It's also the way you write these symbols on blackboards or in
handwriting.
I'll use these number systems informally based on your prior experience with them; actually constructing them rigorously is pretty involved and belongs in other courses (though we can use matrices to construct the complex numbers from the real numbers).
You can specify a finite set by listing its elements, placed between braces ("curly brackets"). Here's a set consisting of 5 elements:
![]()
A set does not have duplicate elements, so don't write things like
"![]() ". The order in which you list the
elements doesn't matter:
". The order in which you list the
elements doesn't matter: ![]() is the same set as
is the same set as ![]() . (It's like a bag of stuff, as we noted at the
start.)
. (It's like a bag of stuff, as we noted at the
start.)
Sets can have other sets as elements:
![]()
You can picture this set as a bag. Inside the bag are 1, 2, and another bag which contains 3 and 4. The number of elements in this set is 3; in other words, in determining the number of elements in a big set, you don't peek inside any little sets inside the the big set.
You can sometimes specify infinite sets by listing elements:
![]()
Most people would assume that you mean the elements to continue 5, 6,
7, and so on. Of course, when you do this you're assuming that the
"pattern" the elements follow is clear; the "![]() " means "continue in the same way". But there's some
ambiguity here; perhaps the elements of the set above are actually
" means "continue in the same way". But there's some
ambiguity here; perhaps the elements of the set above are actually
![]()
If there's any chance of confusion, it's better to use set constructor notation to make the "pattern" the elements follow explicit. Set constructor notation has the form
![]()
The braces "![]() " and "
" and "![]() " indicate that we're
building a set, and its name is T. (You may give a set a
name to make it easier to talk about, but the name isn't required.)
The first part "
" indicate that we're
building a set, and its name is T. (You may give a set a
name to make it easier to talk about, but the name isn't required.)
The first part "![]() " tells us that the elements of T come
from some "big set" S. And "
" tells us that the elements of T come
from some "big set" S. And "![]() " is some
property that a typical element x must satisfy to belong to T.
" is some
property that a typical element x must satisfy to belong to T.
For example, this is the set of positive integers:
![]()
This is the set of positive real numbers:
![]()
You can see how the specification of the "big set" from
which the elements come (![]() or
or ![]() ) can be important.
) can be important.
Sometimes it's convenient to relax the rules for set constructor notation a bit. Here's the set of even integers:
![]()
It says that even integers are integers which are twice another integer. We can save writing (and a variable) by writing the set this way:
![]()
This says even integers are numbers which are twice another integer. Since twice an integer is automatically an integer, the word "numbers" must mean "integers".
We'll often use this kind of shortcut in writing sets. Here's another
example. It's the set of all points on the graph of ![]() in the x-y-plane:
in the x-y-plane:
![]()
Example. Consider the following set of integers:
![]()
(a) Is 46 an element of S?
(b) Is 17 an element of S?
(a) 46 is an element of S, since ![]() and
and ![]() .
.![]()
(b) 17 is not an element of S. Suppose on the contrary that ![]() . Then
. Then ![]() for some
for some ![]() . Subtracting 1 from both sides, I
get
. Subtracting 1 from both sides, I
get ![]() for some integer n. This is impossible, since 16 is
not "evenly divisible" by 3.
for some integer n. This is impossible, since 16 is
not "evenly divisible" by 3.![]()
You may have seen the notations ![]() and
and ![]() in a multivariable
calculus course.
in a multivariable
calculus course. ![]() is the set of ordered pairs of real
numbers, like
is the set of ordered pairs of real
numbers, like ![]() or
or ![]() --- the "x-y
plane". Likewise,
--- the "x-y
plane". Likewise, ![]() is the set of ordered triples of real
numbers, like
is the set of ordered triples of real
numbers, like ![]() or
or ![]() --- 3-dimensional space. Using set constructor
notation, you can write these sets like this:
--- 3-dimensional space. Using set constructor
notation, you can write these sets like this:
![]()
Arbitrary collections of objects.
In some cases, we'll need to deal with collections of objects which aren't finite, but are infinite "in a big way". This presents notational issues, which I'll discuss here. The objects might be elements of a sets, or they might be sets themselves.
If we have just two objects, we could call them x and y. If we have a
small finite number of objects, we can use numerical subscripts. For
instance, for 5 objects, we could use ![]() ,
, ![]() ,
,
![]() ,
, ![]() , and
, and ![]() .
.
If we have a finite number of objects but the number is undetermined
--- say there are n of them --- we can still use subscripts: ![]() ,
,
![]() , ...
, ... ![]() .
.
If we have an infinite but countable number of objects, we can continue to use natural numbers as subscripts:
![]()
The "![]() " on the right indicates that the number of
objects is infinite.
" on the right indicates that the number of
objects is infinite.
In fact, you can take " countable" to mean that the objects are either finite in number, or can be arranged in a sequential list as above. If the objects can't be arranged in a sequential list as above, the objects are uncountable. Thus, if you have an uncountable number of objects, you can't use natural number subscripts to index them. For example, suppose the objects are the real numbers. You can't arrange the real numbers in a sequential list.
So how do we describe an uncountable collection of objects?
To handle this kind of situation is actually simple. We take an index
set --- say I. We don't assume anything about the size of I, or what
its elements look like. We use the elements of I as subscripts for
our objects. So if we're discussing a particular object indexed by I,
we refer to "![]() , where
, where ![]() ". If we need another
object indexed by I, we say "
". If we need another
object indexed by I, we say "![]() , where
, where ![]() ". If we need
4 such objects, we can use subscripts with subscripts, this way:
". If we need
4 such objects, we can use subscripts with subscripts, this way:
![]()
If we wanted 4 possibly different objects, we'd have to
specify that ![]() ,
, ![]() ,
, ![]() , and
, and ![]() are distinct (though
maybe in a given situation our collection of objects contains
duplicates, so different i's might still give the same object).
are distinct (though
maybe in a given situation our collection of objects contains
duplicates, so different i's might still give the same object).
In these cases, we're not saying what i, j, ![]() ,
, ![]() ,
,
![]() , or
, or ![]() are, beyond that they're elements of I, and that I is
some set.
are, beyond that they're elements of I, and that I is
some set.
Arbitrary intersections and unions.
As examples of arbitrary collections of objects, we'll discuss arbitrary unions and intersections of sets. Begin
with an arbitrary collection of sets ![]() . This
means that each
. This
means that each ![]() is a set, and there is one such set for each element
i in the index set I. The index set I might be finite, or if it is
infinite, it might be countable or uncountable.
is a set, and there is one such set for each element
i in the index set I. The index set I might be finite, or if it is
infinite, it might be countable or uncountable.
The intersection of the sets ![]() is denoted
is denoted ![]() . By
definition, an element x is in
. By
definition, an element x is in ![]() if and only if x is in
if and only if x is in ![]() for all
for all ![]() . In other words,
. In other words,
![]()
The big intersection symbol ![]() is like a summation symbol ("
is like a summation symbol ("![]() ") that you've probably seen
elsewhere.
") that you've probably seen
elsewhere.
For just two sets U and V, the definition would say ![]() if and only if
if and only if ![]() and
and ![]() . This agrees with the
definition of "intersection" we gave earlier.
. This agrees with the
definition of "intersection" we gave earlier.
In similar fashion, the union of the sets ![]() is denoted
is denoted ![]() . By
definition, an element x is in
. By
definition, an element x is in ![]() if and only if x is in
if and only if x is in ![]() for some
for some ![]() . ("For some" means "for at least one".) In other
words,
. ("For some" means "for at least one".) In other
words,
![]()
We won't have to deal with arbitrary intersections and unions that often, so don't worry if this seems a bit abstract. When it comes up, you'll see that the notation isn't that difficult to handle.
Copyright 2022 by Bruce Ikenaga