The Span of a Set of Vectors

If you take a set of vectors in a vector space, there's no reason why that set of vectors should be a subspace. For instance, consider the following vectors in the $\real$ -vector space $\real^3$ :

$$\{(1, 3, 2),\ (-5, 1, 0),\ (-4, 4, 2)\}.$$

Now $(1, 3, 2) + (-5, 1, 0) = (-4, 4, 2)$ , which is in the set. But $(-5, 1, 0) + (-4, 4, 2) = (-9, 5, 2)$ is not in the set, so the set is not closed under vector addition. And $2 \cdot (1, 3, 2) = (2, 6, 4)$ is not in the set, so the set is not closed under scalar multiplication. The set is not a subspace of $\real^3$ .

Suppose we try to fix this by finding a subspace of $\real^3$ which contains the three vectors. Well, that's easy: We could take $\real^3$ ! This would work for any set of vectors in $\real^3$ , but for that reason, it isn't a very interesting answer.

It might be better to ask for the "smallest" subspace of $\real^3$ which contains the three vectors. This set will be called the span of the given set of vectors. We might approach this by asking: What vectors do we need to add to the set of three vectors to make it a subspace? Since subspaces are closed under vector addition, we'll need to throw in all the vectors which you get by adding the three vectors. You can check that we'd need to throw in two more vectors, so we now have 5. But subspaces are also closed under scalar multiplication, so we need to throw in multiples of these 5 vectors by every element of $\real$ . Now we have an infinite number of vectors. Oops! We need to ensure that the set is closed under addition, so we need to go back and throw in all sums of the infinitely many vectors we have so far. Then, since we threw in some additional vectors, we need to take scalar multiples of those, and ... .

Our approach is a reasonable one, but we clearly need a more systematic way of carrying it out. We will see how to do it in this section.

Building subspaces involves forming sums and scalar multiples. Rather than thinking of doing these two operations separately, we'll define a concept which does both at once.

Definition. If $v_1$ , $v_2$ , ..., $v_n$ are vectors in a vector space V over a field F, a linear combination of the v's is a vector

$$k_1 v_1 + k_2 v_2 + \cdots + k_n v_n \quad\hbox{for}\quad k_1, k_2, \ldots k_n \in F.$$

Notice that if you take two vectors $v_1$ and $v_2$ and take the scalars to be $k_1 = 1$ and $k_2 = 1$ , you get $v_1 + v_2$ , which is vector addition. And if you just take one vector $v_1$ , then $k_1 v_1$ represents a scalar multiple of that vector. Thus, the idea of a linear combination contains the operations of vector addition and scalar multiplication, but allows us to do many such operations all at once.

Let's see a numerical example. Take $u = (1, 2)$ and $v = (-3, 7)$ in $\real^2$ . Here is a linear combination of u and v:

$$2 u - 5 v = 2 \cdot (1, 2) - 5 \cdot (-3, 7) = (17, -31).$$

$(\sqrt{2} - 17) u + \dfrac{\pi^2}{4} v$ is also a linear combination of u and v. And u and v are themselves linear combinations of u and v, as is the zero vector:

$$u = 1\cdot u + 0 \cdot v, \quad v = 0 \cdot u + 1 \cdot v, \quad 0 = 0 \cdot u + 0 \cdot v.$$

On the other hand, there are vectors in $\real^2$ which are not linear combinations of $p = (1, -2)$ and $q = (-2, 4)$ . Do you see how this pair is different from the first?

Definition. If S is a set of vectors in a vector space V, the span $\langle S \rangle$ of S is the set of all linear combinations of vectors in S.

Remark. $\langle S \rangle$ is also referred to as the subspace generated by S.

If S is a subset of a subspace W, then S spans W (or S is a spanning set for W, or S generates W) if $W = \langle S \rangle$ .

If S is a finite set of vectors, we could just describe $\langle S \rangle$ as the set of all linear combinations of the elements of S. If S is infinite, a particular linear combination of vectors from S involves finitely many vectors from S --- we "grab" finitely many vectors from S at a time --- but we're doing this in all possible ways.

Note that $S \subset \langle S \rangle$ . For if s is a vector in S, then $1 \cdot s = s$ is a linear combination of a vector from S, so it is in $\langle S \rangle$ .

Here's a pictorial example in $\real^2$ . Take two vectors u and v:

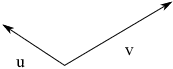
$$\hbox{\epsfysize=0.6in \epsffile{span-1.eps}}$$

It turns out that the span of u and v is all of $\real^2$ ; that is, if $w \in \real^2$ , then w can be written as a linear combination of u and v. To see why this is reasonable, take a vector w and "project" w onto the lines containing the vectors u and v:

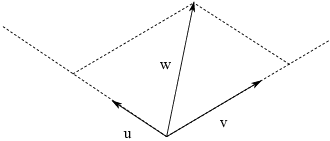
$$\hbox{\epsfysize=1.25in \epsffile{span-2.eps}}$$

I can scale u up by multiplying by an appropriate number to get a vector $a u$ which is the projection of w on the line of u. Likewise, I can scale v up by multiplying by an appropriate number to get a vector $b v$ which is the projection of w on the line of v.

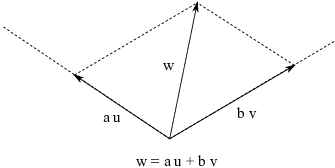
$$\hbox{\epsfysize=1.5in \epsffile{span-3.eps}}$$

As you can see in the picture, w is the diagonal of the parallelogram whose sides are $a u$ and $b v$ , so $w = a u + b v$ .

Try this with some other vectors in place of w. Of course, a picture isn't a proof, but this example should help you get an idea of what the span of a set of vectors means geometrically.

Theorem. If S is a subset of a vector space V, the span $\langle S \rangle$ of S is a subspace of V which contains S.

Proof. We already observed that $S \subset \langle S \rangle$ .

Here are typical elements of the span of S:

$$j_1 u_1 + j_2 u_2 + \cdots + j_n u_n, \quad k_1 v_1 + k_2 v_2 + \cdots + k_n v_n.$$

Here the j's and k's are scalars and the u's and v's are elements of S.

Take two elements of the span and add them:

$$(j_1 u_1 + j_2 u_2 + \cdots + j_nu_n) + (k_1 v_1 + k_2 v_2 + \cdots + k_mv_m) = j_1 u_1 + j_2 u_2 + \cdots + j_nu_n + k_1 v_1 + k_2 v_2 + \cdots + k_mv_m.$$

This sum is an element of the span, because it's a sum of vectors in S, each multiplied by a scalar --- that is, a linear combination of elements of S. Thus, the span is closed under taking sums.

Take an element of the span and multiply it by a scalar:

$$k \cdot (k_1 v_1 + k_2 v_2 + \cdots k_n v_n) = k k_1 v_1 + k k_2 v_2 + \cdots + k k_n v_n.$$

This is an element of the span, because it's a linear combination of elements of S. Thus, the span is closed under scalar multiplication.

Therefore, the span is a subspace.

Example. Prove that the span of $(3, 1, 0)$ and $(2, 1, 0)$ in $\real^3$ is

$$V = \left\{(a, b, 0) \mid a, b \in \real\right\}.$$

To show that two sets are equal, you need to show that each is contained in the other. To do this, take a typical element of the first set and show that it's in the second set. Then take a typical element of the second set and show that it's in the first set.

Let W be the span of $(3, 1, 0)$ and $(2, 1, 0)$ in $\real^3$ . A typical element of W is a linear combination of the two vectors:

$$x \cdot (3, 1, 0) + y \cdot (2, 1, 0) = (3 x + 2 y, x + y, 0).$$

Since the sum is a vector of the form $(a, b, 0)$ for $a, b \in \real$ , it is in V. This proves that $W \subset V$ .

Now let $(a, b, 0) \in V$ . I have to show that this vector is a linear combination of $(3, 1, 0)$ and $\langle 2, 1, 0)$ . This means that I have to find real numbers x and y such that

$$x \cdot (3, 1, 0) + y \cdot (2, 1, 0) = (a, b, 0).$$

If I write the vectors as column vectors, I get

$$x \cdot \left[\matrix{3 \cr 1 \cr 0 \cr}\right] + y \cdot \left[\matrix{2 \cr 1 \cr 0 \cr}\right] = \left[\matrix{a \cr b \cr 0 \cr}\right].$$

I can write this as the matrix equation

$$\left[\matrix{ 3 & 2 \cr 1 & 1 \cr 0 & 0 \cr}\right] \left[\matrix{x \cr y \cr}\right] = \left[\matrix{a \cr b \cr 0 \cr}\right].$$

If I solve this system by row reduction, I get

$$\left[\matrix{ 3 & 2 & a \cr 1 & 1 & b \cr 0 & 0 & 0 \cr}\right] \quad \to \quad \left[\matrix{ 1 & 0 & a - 2 b \cr 0 & 1 & -a + 3 b \cr 0 & 0 & 0 \cr}\right]$$

The solution is

$$x = a - 2 b, \quad y = -a + 3 b.$$

In other words,

$$(a - 2 b) \cdot (3, 1, 0) + (-a + 3 b) \cdot (2, 1, 0) = (a, b, 0).$$

Since $(a, b, 0)$ is a linear combination of $(3, 1, 0)$ and $(2, 1, 0)$ , it follows that $(a, b, 0) \in W$ . This proves that $V \subset W$ .

Since $W \subset V$ and $V \subset W$ , I have $W = V$ .

Example. Let

$$S = \left\{(1, 1, 0), (0, 1, 1)\right\} \subset \real^3.$$

(a) Prove or disprove: $(3, -1, -4)$ is in the span of S.

(b) Prove or disprove: $(5, -2, 6)$ is in the span of S.

(a) The vector $(3, -1, 4)$ is in the span of $(1, 1, 0)$ and $(0, 1, 1)$ if it can be written as a linear combination of $(1, 1, 0)$ and $(0, 1, 1)$ . So I try to find numbers a and b such that

$$a \cdot (1, 1, 0) + b \cdot (0, 1, 1) = (3, -1, 4).$$

I'll convert this to a matrix equation by writing the vectors as column vectors:

$$a \cdot \left[\matrix{1 \cr 1 \cr 0 \cr}\right] + b \cdot \left[\matrix{0 \cr 1 \cr 1 \cr}\right] = \left[\matrix{3 \cr -1 \cr -4 \cr}\right].$$

By using column vectors (rather than row vectors), we get a familiar kind of matrix equation:

$$\left[\matrix{1 & 0 \cr 1 & 1 \cr 0 & 1 \cr}\right] \left[\matrix{a \cr b \cr}\right] = \left[\matrix{3 \cr -1 \cr -4 \cr}\right].$$

We can solve for a and b by row reducing the augmented matrix:

$$\left[\matrix{ 1 & 0 & 3 \cr 1 & 1 & -1 \cr 0 & 1 & -4 \cr}\right] \quad \to \quad \left[\matrix{ 1 & 0 & 3 \cr 0 & 1 & -4 \cr 0 & 0 & 0 \cr}\right]$$

The solution is $a = 3$ , $b = -4$ . That is,

$$3 \cdot (1, 1, 0) + (-4) \cdot (0, 1, 1) = (3, -1, -4).$$

The vector $(3, -1, -4)$ is in the span of S.

(b) Following the approach we took in part (a), we'll convert the vectors to column vectors to get the equation

$$a \cdot \left[\matrix{1 \cr 1 \cr 0 \cr}\right] + b \cdot \left[\matrix{0 \cr 1 \cr 1 \cr}\right] = \left[\matrix{5 \cr -2 \cr 6 \cr}\right].$$

This is equivalent to the matrix equation

$$\left[\matrix{1 & 0 \cr 1 & 1 \cr 0 & 1 \cr}\right] \left[\matrix{a \cr b \cr}\right] = \left[\matrix{5 \cr -2 \cr 6 \cr}\right].$$

Row reduce to solve the system:

$$\left[\matrix{ 1 & 0 & 5 \cr 1 & 1 & -2 \cr 0 & 1 & 6 \cr}\right] \quad \to \quad \left[\matrix{ 1 & 0 & 0 \cr 0 & 1 & 0 \cr 0 & 0 & 1 \cr}\right]$$

The last matrix says "$0 = 1$ ", a contradiction. The system is inconsistent, so there are no such numbers a and b. Therefore, $(5, -2, 6)$ is not in the span of S.

Thus, to determine whether the vector $b \in F^n$ is in the span of $v_1$ , $v_2$ , ..., $v_m$ in $F^n$ , form the augmented matrix

$$\left[\matrix{\uparrow & \uparrow & & \uparrow & \uparrow \cr v_1 & v_2 & \cdots & v_m & b \cr \downarrow & \downarrow & & \downarrow & \downarrow \cr}\right]$$

If the system has a solution, b is in the span, and coefficients of a linear combination of the v's which add up to b are given by a solution to the system. If the system has no solutions, then b is not in the span of the v's.

(In a general vector space where vectors may not be "numbers in slots", you have to got back to the definition of spanning set.)

Example. Consider the following set of vectors in $\real^3$ :

$$\left\{\left[\matrix{1 \cr 0 \cr -1 \cr}\right], \left[\matrix{2 \cr 1 \cr 3 \cr}\right], \left[\matrix{1 \cr 1 \cr -4 \cr}\right]\right\}$$

Prove that the span of the set is all of $\real^3$ .

I have to show that any vector $(x, y, z) \in \real^3$ can be written as a linear combination of the vectors in the set. That is, I must find real numbers a, b, c such that

$$a \cdot\left[\matrix{1 \cr 0 \cr -1 \cr}\right] + b \cdot\left[\matrix{2 \cr 1 \cr 3 \cr}\right] + c \cdot\left[\matrix{1 \cr 1 \cr -4 \cr}\right] = \left[\matrix{x \cr y \cr z \cr}\right].$$

The matrix equation is

$$\left[\matrix{ 1 & 2 & 1 \cr 0 & 1 & 1 \cr -1 & 3 & -4 \cr}\right] \left[\matrix{a \cr b \cr c \cr}\right] = \left[\matrix{x \cr y \cr z \cr}\right].$$

Row reduce to solve:

$$\left[\matrix{ 1 & 2 & 1 & x \cr 0 & 1 & 1 & y \cr -1 & 3 & -4 & z \cr}\right] \quad \to \quad \left[\matrix{ 1 & 0 & 0 & \dfrac{1}{8} (7 x - 11 y - z) \cr \noalign{\vskip2pt} 0 & 1 & 0 & \dfrac{1}{8} (x + 3 y + z) \cr \noalign{\vskip2pt} 0 & 0 & 1 & \dfrac{1}{8} (-x + 5 y - z) \cr}\right]$$

I get the ugly solution

$$a = \dfrac{1}{8} (7 x - 11 y - z), \quad b = \dfrac{1}{8} (x + 3 y + z), \quad c = \dfrac{1}{8} (-x + 5 y - z).$$

This shows that, given any vector $(x, y, z)$ , I can find a linear combination of the original three vectors which equals $(x, y, z)$ .

Thus, the span of the original set of three vectors is all of $\real^3$ .

Example. Let

$$S = \left\{(1, 2, 1), (1, 4, 2)\right\} \quad\hbox{in}\quad \integer_5^3.$$

(a) Determine whether $(0, 4, 2) \in \langle S \rangle$ .

(b) Determine whether $(1, 1, 1) \in \langle S \rangle$ .

(a) I want to determine whether there are numbers $a, b \in \integer_5$ such that

$$a \cdot \left[\matrix{1 \cr 2 \cr 1 \cr}\right] + b \cdot \left[\matrix{1 \cr 4 \cr 2 \cr}\right] = \left[\matrix{0 \cr 4 \cr 2 \cr}\right].$$

This gives the system

$$\left[\matrix{1 & 1 \cr 2 & 4 \cr 1 & 2 \cr}\right] \left[\matrix{a \cr b \cr}\right] = \left[\matrix{0 \cr 4 \cr 2 \cr}\right].$$

Form the augmented matrix and row reduce:

$$\left[\matrix{ 1 & 1 & 0 \cr 2 & 4 & 4 \cr 1 & 2 & 2 \cr}\right] \quad \to \quad \left[\matrix{ 1 & 0 & 3 \cr 0 & 1 & 2 \cr 0 & 0 & 0 \cr}\right]$$

The last matrix says $a = 3$ and $b = 2$ . Therefore, $(0, 4, 2)$ is in the span of S:

$$3 \cdot \left[\matrix{1 \cr 2 \cr 1 \cr}\right] + 2 \cdot \left[\matrix{1 \cr 4 \cr 2 \cr}\right] = \left[\matrix{0 \cr 4 \cr 2 \cr}\right].\quad\halmos$$

(b) I want to determine whether there are numbers $a, b \in \integer_5$ such that

$$a \cdot \left[\matrix{1 \cr 2 \cr 1 \cr}\right] + b \cdot \left[\matrix{1 \cr 4 \cr 2 \cr}\right] = \left[\matrix{1 \cr 1 \cr 1 \cr}\right].$$

This gives the system

$$\left[\matrix{1 & 1 \cr 2 & 4 \cr 1 & 2 \cr}\right] \left[\matrix{a \cr b \cr}\right] = \left[\matrix{1 \cr 1 \cr 1 \cr}\right].$$

Form the augmented matrix and row reduce:

$$\left[\matrix{ 1 & 1 & 1 \cr 2 & 4 & 1 \cr 1 & 2 & 1 \cr}\right] \quad \to \quad \left[\matrix{ 1 & 0 & 0 \cr 0 & 1 & 0 \cr 0 & 0 & 1 \cr}\right]$$

The last row of the row reduced echelon matrix says "$0 = 1$ ". This contradiction implies that the system is has no solutions. Therefore, $(1, 1, 1)$ is not in the span of S.

In the next example, we go back to the definition of the span of a set of vectors, rather than writing down a matrix equation.

Example. $C(\real)$ is the vector space over $\real$ of continuous functions $\real \to \real$ . Let

$$f(x) = \sin x, \quad g(x) = e^x, \quad h(x) = x^2.$$

Show that h is not in $\langle f, g \rangle$ , the span of f and g.

We'll give a proof by contradiction.

Suppose there are numbers $a, b \in \real$ such that

$$x^2 = a \sin x + b e^x \quad\hbox{for all}\quad x \in \real.$$

Set $x = 0$ . We get

$$0^2 = a \sin 0 + b e^0, \quad\hbox{so}\quad 0 = b.$$

The equation becomes

$$x^2 = a \sin x.$$

Set $x = \dfrac{\pi}{2}$ . We get

$$\left(\dfrac{\pi}{2}\right)^2 = a \sin \dfrac{\pi}{2}, \quad\hbox{so}\quad \dfrac{\pi^2}{4} = a.$$

The equation is now

$$x^2 = \dfrac{\pi^2}{4} \sin x.$$

Finally, set $x = \dfrac{5 \pi}{2}$ . We get

$$\left(\dfrac{5 \pi}{2}\right)^2 = \dfrac{\pi^2}{4} \sin \dfrac{5 \pi}{2}, \quad\hbox{or}\quad \dfrac{25 \pi^2}{4} = \dfrac{\pi^2}{4}, \quad\hbox{so}\quad 25 = 1.$$

This contradiction shows there are no numbers $a, b \in \real$ which make the initial equation true. Hence, h is not in the span of f and g.

Another definition of the span of a set

There is another way to define the span of a set of vectors. The construction is a little more subtle than the one we gave earlier. It uses the intersection of a (possibly) infinite collection of subspaces, which we know by an earlier result is a subspace.

Let V be a vector space over a field F, and let S be a set of vectors in V. Let

$$\tilde{S} = \bigcap \{W \mid S \subset W \hbox{ and } W \hbox{ is a subspace of } V\}.$$

That is, to form $\tilde{S}$ we intersect all subspaces of V which contain S. Note that there is at least one subspace that contains S, namely V itself. We will show that $\tilde{S}$ is just the span of S, as constructed earlier: The set of all linear combinations of elements of S.

(By the way, "$\tilde{S}$ " is just temporary notation I'm using for this discussion. After this, I'll just use $\langle S \rangle$ to denote the span of S.)

Theorem. $\tilde{S} = \langle S \rangle$ .

Proof. First, the span $\langle S \rangle$ is a subspace of V which contains S. So $\langle S \rangle$ is one of the subspaces being intersected to construct $\tilde{S}$ , and hence

$$\tilde{S} = \bigcap \{W \mid S \subset W \hbox{ and } W \hbox{ is a subspace of } V\} \subset \langle S \rangle.$$

To complete the proof, I'll show that $\langle S \rangle \subset \tilde{S}$ . Take an element of $\langle S \rangle$ , namely a linear combination of elements of S:

$$a_1 s_1 + a_s s_2 + \cdots + a_n s_n \quad\hbox{where}\quad a_i \in F \quad\hbox{and}\quad s_i \in S.$$

Let W be a subspace of V which contains S. Then $s_1, s_2, \ldots s_n \in W$ , and since W is a subspace,

$$a_1 s_1 + a_s s_2 + \cdots + a_n s_n \in W.$$

Thus, $a_1 s_1 + a_s s_2 + \cdots + a_n s_n$ is contained in every subspace which contains S --- that is, it is contained in every subspace being intersected to construct $\tilde{S}$ . Hence, it is contained in $\tilde{S}$ . This proves that $\langle S \rangle \subset \tilde{S}$ .

Therefore, $\tilde{S} = \langle S \rangle$ .

If you want to construct an object in math using some "building blocks", there are often two general ways to do so. The first way is to start with the building blocks, and combine them to build the object "from the inside out". This direct approach is what we did in the definition of $\langle S \rangle$ as all linear combinations of elements of S. It requires that you know how to put the blocks together to do the "building".

Another approach is to take all objects of the "right kind" which contain the building blocks and find the "smallest". You find the "smallest" such object by intersecting all the objects of the "right kind" containing the building blocks. In this approach, you will usually have to intersect an infinite number of sets. And you will need to show that the intersection of sets of the "right kind" is still a set of the "right kind". This is the approach we used in intersecting all subspaces containing S.

Of course, if you've done things correctly, the two approaches give the same object at the end, as they did here. Both approaches are useful in mathematics.

Contact information

Bruce Ikenaga's Home Page

Copyright 2022 by Bruce Ikenaga