Subspaces

Definition. Let V be a vector space over a field F, and let $W \subset V$ , $W \ne \emptyset$ . W is a subspace of V if:

(a) If $u, v \in W$ , then $u + v \in W$ .

(b) If $k \in F$ and $u \in W$ , then $k u \in W$ .

In other words, W is closed under addition of vectors and under scalar multiplication.

If we draw the vectors as arrows, we can picture the axioms in this way:

$$\hbox{\epsfysize=1.5in \epsffile{subspaces-0.eps}}$$

Remember that not all vectors can be drawn as arrows, so in general these pictures are just aids to your intuition.

A subspace W of a vector space V is itself a vector space, using the vector addition and scalar multiplication operations from V. If you go through the axioms for a vector space, you'll see that they all hold in W because they hold in V, and W is contained in V. Thus, the subspace axioms simply ensure that the vector addition and scalar multiplication operations from V "don't take you outside of W" when applied to vectors in W.

Remark. If W is a subspace, then axiom (a) says that sum of two vectors in W is in W. You can show using induction that if $x_1, \ldots, x_n \in W$ , then $x_1 + \cdots + x_n \in W$ for any $n \ge 1$ .

What do subspaces "look like"?

The subspaces of the plane $\real^2$ are $\{0\}$ , $\real^2$ , and lines passing through the origin. In the picture below, the lines A and B are subspaces of $\real^2$ .

$$\hbox{\epsfysize=1.5in \epsffile{subspaces-1.eps}}$$

In $\real^3$ , the subspaces are the $\{0\}$ , $\real^3$ , and lines or planes passing through the origin.

$$\hbox{\epsfysize=2in \epsffile{subspaces-2.eps}}$$

Similar statements hold for $\real^n$ .

We'll see below that a subspace must contain the zero vector, which explains why the examples I just gave are sets which pass through the origin.

As we've seen earlier, you get very different pictures of vectors when F is a field other than $\real$ . In these cases, pictures for subspaces are also different. For example, consider the following subspace of $\integer_5^2$ :

$$S = \{(0, 0), (2, 3), (4, 1), (1, 4), (3, 2)\}.$$

Here's a picture, with the gray dots denoting the 5 points of S:

$$\hbox{\epsfysize=1.25in \epsffile{subspaces-3.eps}}$$

While 4 of the points lie on a "line", the "line" is not a line through the origin. The origin is in S, but it doesn't lie on the same "line" as the other points.

Or consider the vector space $C(\real)$ over $\real$ , consisting of continuous functions $\real \to \real$ . There is a subspace consisting of all multiples of $e^x$ --- so things like $2 e^x$ , $-\pi e^x$ , $1.79132 e^x$ , $0 \cdot e^x$ , and so on. Here's a picture which shows the graph of some of the elements of this subspace:

$$\hbox{\epsfysize=1.75in \epsffile{subspaces-4.eps}}$$

Of course, there are actually an infinite number of "graphs" (functions) in this subspace --- I've only drawn a few. You can see our subspace is pretty far from "a line through the origin", even though it consists of all multiples of a single vector.

In what follows, we'll look at properties of subspaces, and discuss how to check whether a set is or is not a subspace.

First, every vector space contains at least two "obvious" subspaces, as described in the next result.

Proposition. if V is a vector space over a field F, then $\{0\}$ and V are subspaces of V.

Proof. I'll do the proof for $\{0\}$ by way of example. First, I have to take two vectors in $\{0\}$ and show that their sum is in $\{0\}$ . But $\{0\}$ contains only the zero vector 0, so my "two" vectors are 0 and 0 --- and $0 + 0 = 0$ , which is in $\{0\}$ .

Next, I have to take $k \in F$ and a vector in $\{0\}$ --- which, as I just saw, must be 0 --- and show that their product is in $\{0\}$ . But $k \cdot 0 = 0 \in \{0\}$ . This verifies the second axiom, and so $\{0\}$ is a subspace.

Obviously, the very uninteresting vector space consisting of just a zero vector (i.e. $V = \{0\}$ ) has only the one subspace $V = \{0\}$ .

If a vector space V is nonzero and one-dimensional --- roughly speaking, if V "looks like" a line --- then $\{0\}$ and V are the only subspaces, and they are distinct. In this case, V consists of all multiples $k v$ of any nonzero vector $v \in V$ by all scalars $k \in F$ .

Beyond those cases, a vector space V always has subspaces other than $\{0\}$ and V. For example, if $V \ne 0$ , take a nonzero vector $x \in V$ and consider the set of all multiples $k x$ of x by scalars $k \in F$ . You can check that this is a subspace --- the "line" passing through x.

If you want to show that a subset of a vector space is a subspace, you can combine the verifications for the two subspace axioms into a single verification.

Proposition. Let V be a vector space over a field F, and let W be a subset of V.

W is a subspace of V if and only if $u, v \in W$ and $k \in F$ implies $k u + v \in W$ .

Proof. Suppose W is a subspace of V, and let $u, v \in W$ and $k \in F$ . Since W is closed under scalar multiplication, $k u \in W$ . Since W is closed under vector addition, $k u + v \in W$ .

Conversely, suppose $u, v \in W$ and $k \in F$ implies $k u + v \in W$ . Take $k = 1$ : Our assumption says that if $u, v \in W$ , then $u + v \in W$ . This proves that W is closed under vector addition. Again in our assumption, take $v = 0$ . The assumption then says that if $u \in W$ and $k \in F$ , then $k u \in W$ . This proves that W is closed under scalar multiplication. Hence, W is a subspace.

Note that the two axioms for a subspace are independent: Both can be true, both can be false, or one can be true and the other false. Hence, some of our examples will ask that you check each axiom separately, proving that it holds if it's true and disproving it by a counterexample if it's false.

Lemma. Let W be a subspace of a vector space V.

(a) The zero vector is in W.

(b) If $w \in W$ , then $-w \in W$ .

Note: These are not part of the axioms for a subspace: They are properties a subspace must have. So if you are checking the axioms for a subspace, you don't need to check these properties. But on the other hand, if a subset does not have one of these properties (e.g. the subset doesn't contain the zero vector), then it can't be a subspace.

Proof. (a) Take any vector $w \in W$ (which you can do because W is nonempty), and take $0 \in F$ . Since W is closed under scalar multiplication, $0 \cdot w \in W$ . But $0 \cdot w = 0$ , so $0 \in W$ .

(b) Since $w \in W$ and $-1 \in F$ , $(-1) \cdot w = -w$ is in W.

Example. Consider the real vector space $\real^2$ , the usual x-y plane.

(a) Show that the following sets are subspaces of $\real^2$ :

$$W_1 = \{(x, 0) \mid x \in \real\} \quad\hbox{and}\quad W_2 = \{(0, y) \mid y \in \real\}$$

(These are just the x and y-axes.)

(b) Show that the union $W_1 \cup W_2$ is not a subspace.

(a) I'll check that $W_1$ is a subspace. (The proof for $W_2$ is similar.) First, I have to show that two elements of $W_1$ add to an element of $W_1$ . An element of $W_1$ is a pair with the second component 0. So $(x_1, 0)$ , $(x_2, 0)$ are two arbitrary elements of $W_1$ . Add them:

$$(x_1, 0) + (x_2, 0) = (x_1 + x_2, 0).$$

$(x_1 + x_2, 0)$ is in $W_1$ , because its second component is 0. Thus, $W_1$ is closed under sums.

Next, I have to show that $W_1$ is closed under scalar multiplication. Take a scalar $k \in \real$ and a vector $(x, 0) \in W_1$ . Take their product:

$$k \cdot (x, 0) = (k x, 0).$$

The product $(k x, 0)$ is in $W_1$ because its second component is 0. Therefore, $W_1$ is closed under scalar multiplication.

Thus, $W_1$ is a subspace.

Notice that in doing the proof, I did not use specific vectors in $W_1$ like $(42, 0)$ or $(-17, 0)$ . I'm trying to prove statements about arbitrary elements of $W_1$ , so I use "variable" elements.

(b) I'll show that $W_1 \cup W_2$ is not closed under vector addition. Remember that the union of two sets consists of everything in the first set or in the second set (or in both). Thus, $(3, 0) \in W_1 \cup W_2$ , because $(3, 0) \in W_1$ . And $(0, 17) \in W_1 \cup W_2$ , because $(0, 17) \in W_2$ . But

$$(3, 0) + (0, 17) = (3, 17) \not\in W_1 \cup W_2.$$

$(3, 17) \not\in W_1$ because its second component isn't 0. And $(3, 17) \not\in W_2$ because its first component isn't 0. Since $(3, 17)$ isn't in either $W_1$ or $W_2$ , it's not in their union.

Pictorially, it's easy to see: $(3, 17)$ doesn't lie in either the x-axis ($W_1$ ) or the y-axis ($W_2$ ):

$$\hbox{\epsfysize=1.5in \epsffile{subspaces-5.eps}}$$

Thus, $W_1 \cup W_2$ is not a subspace.

You can check, however, that $W_1 \cup W_2$ is closed under scalar multiplication: Multiplying a vector on the x-axis by a number gives another vector on the x-axis, and multiplying a vector on the y-axis by a number gives another vector on the y-axis.

The last example shows that the union of subspaces is not in general a subspace. However, the intersection of subspaces is a subspace, as we'll see later.

Example. Prove or disprove: The following subset of $\real^3$ is a subspace of $\real^3$ :

$$W = \{(x, y, 1) \mid x, y \in \real\}.$$

If you're trying to decide whether a set is a subspace, it's always good to check whether it contains the zero vector before you start checking the axioms. In this case, the set consists of 3-dimensional vectors whose third components are equal to 1. Obviously, the zero vector $(0, 0, 0)$ doesn't satisfy this condition.

Since W doesn't contain the zero vector, it's not a subspace of $\real^3$ .

Example. Consider the following subset of the vector space $\real^2$ :

$$W = \left\{(x, \sin x) \mid x \in \real\right\}.$$

Check each axiom for a subspace (i.e. closure under addition and closure under scalar multiplication). If the axiom holds, prove it; if the axiom doesn't hold, give a specific counterexample.

Notice that this problem is open-ended, in that you aren't told at the start whether a given axiom holds or not. So you have to decide whether you're going to try to prove that the axiom holds, or whether you're going to try to find a counterexample. In these kinds of situations, look at the statement of the problem --- in this case, the definition of W. See if your mathematical experience causes you to lean one way or another --- if so, try that approach first.

If you can't make up your mind, pick either "prove" or "disprove" and get started! Usually, if you pick the wrong approach you'll know it pretty quickly --- in fact, getting stuck taking the wrong approach may give you an idea of how to make the right approach work.

Suppose I start by trying to prove that the set is closed under sums. I take two vectors in W --- say $(x, \sin x)$ and $(y, \sin y)$ . I add them:

$$(x, \sin x) + (y, \sin y) = (x + y, \sin x + \sin y).$$

The last vector isn't in the right form --- it would be if $\sin x + \sin y$ was equal to $\sin (x + y)$ . Based on your knowledge of trigonometry, you should know that doesn't sound right. You might reason that if a simple identity like "$\sin x + \sin y = \sin (x + y)$ " was true, you probably would have learned about it!

I now suspect that the sum axiom doesn't hold. I need a specific counterexample --- that is, two vectors in W whose sum is not in W.

To choose things for a counterexample, you should try to choose things which are not too "special" or your "counterexample" might accidentally satisfy the axiom, which is not what you want. At the same time, you should avoid things which are too "ugly", because it makes the counterexample less convincing if a computer is needed (for instance) to compute the numbers. You may need a few tries to find a good counterexample. Remember that the things in your counterexample should involve specific numbers, not "variables".

Returning to our problem, I need two vectors in W whose sum isn't in W. I'll use $\left(\dfrac{\pi}{2}, \sin \dfrac{\pi}{2}\right)$ and $(\pi, \sin \pi)$ . Note that

$$\left(\dfrac{\pi}{2}, \sin \dfrac{\pi}{2}\right) = \left(\dfrac{\pi}{2}, 1\right) \in W \quad\hbox{and}\quad (\pi, \sin \pi) = (\pi, 0) \in W.$$

On the other hand,

$$\left(\dfrac{\pi}{2}, \sin \dfrac{\pi}{2}\right) + (\pi, \sin \pi) = \left(\dfrac{\pi}{2}, 1\right) + (\pi, 0) = \left(\dfrac{3 \pi}{2}, 1\right).$$

But $\left(\dfrac{3 \pi}{2}, 1\right) \not\in W$ because $\sin \dfrac{3 \pi}{2} = -1 \ne 1$ .

How did I choose the two vectors? I decided to use a multiple of $\pi$ in the first component, because the sine of a multiple of $\pi$ (in the second component) comes out to "nice numbers". If I had used (say) $(1, \sin 1)$ , I'd have needed a computer to tell me that $\sin 1 \approx 0.841470984808 \ldots$ , and a counterexample would have looked kind of ugly. In addition, an approximation of this kind really isn't a proof.

How did I know to use $\dfrac{\pi}{2}$ and $\pi$ ? Actually, I didn't know till I did the work that these numbers would produce a counterexample --- you often can't know without trying whether the numbers you've chosen will work.

Thus, W is not closed under vector addition, and so it is not a subspace. If that was the question, I'd be done, but I was asked to each axiom. It is possible for one of the axioms to hold even if the other one does not. So I'll consider scalar multiplication.

I'll give a counterexample to show that the scalar multiplication axiom doesn't hold. I need a vector in W; I'll use $\left(\dfrac{\pi}{2}, \sin \dfrac{\pi}{2}\right)$ again. I also need a real number; I'll use 2. Now

$$2 \cdot \left(\dfrac{\pi}{2}, \sin \dfrac{\pi}{2}\right) = \left(\pi, 2 \sin \dfrac{\pi}{2}\right) = (\pi, 2).$$

But $(\pi, 2) \not\in W$ , because $\sin \pi = 0 \ne 2$ .

Thus, neither the addition axiom nor the scalar multiplication axiom holds. Obviously, W is not a subspace.

Example. Let F be a field, and let $A, B \in M(n, F)$ . Consider the following subset of $F^n$ :

$$W = \{v \in F^n \mid A v = B v\}.$$

Show that W is a subspace of $F^n$ .

This set is defined by a property rather than by appearance, and axiom checks for this kind of set often give people trouble. The problem is that elements of W don't "look like" anything --- if you need to refer to a couple of arbitrary elements of W, you might call them u and v (for instance). There's nothing about the symbols u and v which tells you that they belong to W. But u and v are like people who belong to a club: You can't tell from their appearance that they're club members, but you could tell from the property that they both have membership cards.

When you write a proof, you start from assumptions and reason to the conclusion. You should not start with the conclusion and "work backwards". Sometimes reasoning that works in one direction might not work in the opposite direction. For example, suppose x is a real number. If $x = 1$ , then $x^2 = 1$ . But if $x^2 = 1$ , it doesn't follow that $x = 1$ --- maybe $x = -1$ .

Reasoning in mathematics is deductive, not confirmational.

In this problem, to check closure under addition, you assume that u and v and in W, and show that $u + v$ is in W. You do not start by assuming that $u + v$ is in W.

Nevertheless, in deciding how to do a proof, it's okay to work backwards "on scratch paper" to figure out what to do. Here's a way of sketching out a proof that allows you to work backward while ensuring that the steps work forward as well.

Start by putting down the assumptions $u \in W$ and $v \in W$ at the top and the conclusion $u + v \in W$ at the bottom. Leave space in between to work.

$$\hbox{\epsfysize=1in \epsffile{subspaces-6.eps}}$$

Next, use the definition of W to translate each of the statements: $u \in W$ means $A u = B u$ , so put "$A u = B u$ " below "$u \in W$ ". Likewise, $v \in W$ means $A v = B v$ , so put "$A v = B v$ " below "$v \in W$ ". On the other hand, $u + v \in W$ means $A(u + v) = B(u + v)$ , but since "$u + v \in W$ " is what we want to conclude, put "$A(u + v) = B(u + v)$ " above "$u + v \in W$ ".

$$\hbox{\epsfysize=1in \epsffile{subspaces-7.eps}}$$

At this point, you can either work downwards from $A u = B u$ and $A v = B v$ , or upwards from $A(u + v) = B(u + v)$ . But if you work upwards from $A(u + v) = B(u + v)$ , you must ensure that the algebra you do is reversible --- that it works downwards as well.

I'll work downwards from $A u = B u$ and $A v = B v$ . What algebra could I do which would get me closer to $A(u + v) = B(u + v)$ ? Since the target involves addition, it's natural to add the equations:

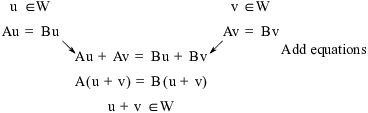
$$\hbox{\epsfysize=1in \epsffile{subspaces-8.eps}}$$

At this point, I'm almost done. To finish, I have to explain how to go from $A u + A v = B u + B v$ to $A(u + v) = B(u + v)$ . You can see that I just need to factor A out of the left side and factor B out of the right side:

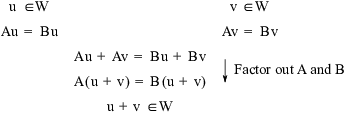
$$\hbox{\epsfysize=1in \epsffile{subspaces-9.eps}}$$

The proof is complete! If you were just writing the proof for yourself, the sketch above might be good enough. If you were writing this proof more formally --- say for an assignment or a paper --- you might add some explanatory words.

For instance, you might say: "I need to show that W is closed under addition. Let $u \in W$ and let $v \in W$ . By definition of W, this means that $A u = B u$ and $A v = B v$ . Adding the equations, I get $A u = A v = B u + B v$ . Factoring A out of the left side and B out of the right side, I get $A(u + v) = B(u + v)$ . By definition of W, this means that $u + v \in W$ . Hence, W is closed under addition."

By the way, be careful not to write things like "$A(u + v) + B(u + v) \in W$ " --- do you see why this doesn't make sense? "$A(u + v) = B(u + v)$ " is an equation that $u + v$ satisfies. You can't write "$\in W$ ", since an equation can't be an element of W. Elements of W are vectors. You say "$u + v \in W$ ", as in the last line.

Here's a sketch of a similar "fill-in" proof for closure under scalar multiplication:

$$\hbox{\epsfysize=1.25in \epsffile{subspaces-10.eps}}$$

Try working through the proof yourself.

Example. Consider the following subset of the polynomial ring $\real[x]$ :

$$V = \{f(x) \in \real[x] \mid f(2) = 1\}.$$

Show that V is not a subspace of $\real[x]$ .

The zero polynomial (i.e. the zero vector) is not in V, because the zero polynomial does not give 1 when you plug in $x = 2$ . Hence, V is not a subspace.

Alternatively, the constant polynomial $f(x) = 1$ is an element of V --- it gives 1 when you plug in 2 --- but $2 \cdot f(x)$ is not. So V is not closed under scalar multiplication.

See if you can give an example which shows that V is not closed under vector addition.

Proposition. If A is an $m \times n$ matrix over the field F, consider the set V of n-dimensional vectors x which satisfy

$$A x = 0.$$

Then V is a subspace of $F^n$ .

Proof. Suppose $x, y \in V$ . Then $A x = 0$ and $A y = 0$ , so

$$A(x + y) = A x + A y = 0 + 0 = 0.$$

Hence, $x + y \in V$ .

Suppose $x \in V$ and $k \in F$ . Then $A x = 0$ , so

$$A (k x) = k (A x) = k \cdot 0 = 0.$$

Therefore, $k x \in V$ .

Thus, V is a subspace.

The subspace defined in the last proposition is called the null space of A.

Definition. Let A be an $m \times n$ matrix over the field F.

$$\hbox{null space}(A) = \{x \in F^n \mid A x = 0\}.$$

As a specific example of the last proposition, consider the following system of linear equations over $\real$ :

$$\left[\matrix{ 1 & 1 & 0 & 1 \cr 0 & 0 & 1 & 3 \cr}\right] \left[\matrix{w \cr x \cr y \cr z \cr}\right] = \left[\matrix{0 \cr 0 \cr 0 \cr 0 \cr}\right].$$

You can show by row reduction that the general solution can be written as

$$w = -s - t, \quad x = s, \quad y = -3 t, \quad z = t.$$

Thus,

$$\left[\matrix{w \cr x \cr y \cr z \cr}\right] = \left[\matrix{-s - t \cr s \cr -3 t \cr t \cr}\right].$$

The Proposition says that the set of all vectors of this form constitute a subspace of $\real^4$ .

For example, if you add two vectors of this form, you get another vector of this form:

$$\left[\matrix{-s - t \cr s \cr -3 t \cr t \cr}\right] + \left[\matrix{-s' - t' \cr s' \cr -3 t' \cr t' \cr}\right] = \left[\matrix{-(s + s') - (t + t') \cr s + s' \cr -3(t + t') \cr t + t' \cr}\right].$$

You can check directly that the set is also closed under scalar multiplication.

In terms of systems of linear equations, a vector $(x_1, \ldots, x_n) \in F^n$ is in the null space of the matrix $A = (a_{i j})$ if it's a solution to the system

$$\matrix{ a_{1 1} x_1 & + & \cdots & + & a_{1 n} x_n & = & 0 \cr a_{2 1} x_1 & + & \cdots & + & a_{2 n} x_n & = & 0 \cr & & & \vdots & & & \cr a_{n 1} x_1 & + & \cdots & + & a_{n n} x_n & = & 0 \cr}$$

In this situation, we say that the vectors $(x_1, \ldots, x_n)$ make up the solution space of the system. Since the solution space of the system is another name for the null space of A, the solution space is a subspace of $F^n$ .

We'll study the null space of a matrix in more detail later.

Example. $C(\real)$ denotes the real vector space of continuous functions $\real \to \real$ . Consider the following subset of $C(\real)$ :

$$S = \left\{f \in C(\real) \Bigm| f(x) = \int_0^x e^t f(t)\,dt\right\}.$$

Prove that S is a subspace of $C(\real)$ .

Let $f, g \in S$ . Then

$$f(x) = \int_0^x e^t f(t)\,dt \quad\hbox{and}\quad g(x) = \int_0^x e^t g(t)\,dt.$$

Adding the two equations and using the fact that "the integral of a sum is the sum of the integrals", we have

$$f(x) + g(x) = \int_0^x e^t f(t)\,dt + \int_0^x e^t g(t)\,dt = \int_0^x e^t [f(t) + g(t)]\,dt.$$

This proves that $f(x) + g(x) \in S$ , so S is closed under addition.

Let $f \in S$ , so

$$f(x) = \int_0^x e^t f(t)\,dt.$$

Let $c \in \real$ . Using the fact that constants can be moved into integrals, we have

$$c \cdot f(x) = c \cdot \int_0^x e^t f(t)\,dt = \int_0^x e^t [c \cdot f(t)]\,dt.$$

This proves that $c \cdot f(x) \in S$ , so S is closed under scalar multiplication. Thus, S is a subspace of $C(\real)$ .

Intersections of subspaces.

We've seen that the union of subspaces is not necessarily a subspace. For intersections, the situation is different: The intersection of any number of subspaces is a subspace. The only signficant issue with the proof is that we will deal with an arbitrary collection of sets --- possibly infinite, and possibly uncountable. Except for taking care with the notation, the proof is fairly easy.

Theorem. Let V be a vector space over a field F, and let $\{U_i\}_{i \in I}$ be a collection of subspaces of V. The intersection $\displaystyle \bigcap_{i \in I} U_i$ is a subspace of V.

Proof. We have to show that $\displaystyle \bigcap_{i \in I} U_i$ is closed under vector addition and under scalar multiplication.

Suppose $x, y \in \displaystyle \bigcap_{i \in I} U_i$ . For x and y to be in the intersection of the $U_i$ , they must be in each $U_i$ for all $i \in I$ . So pick a particular $i \in I$ ; we have $x, y \in U_i$ . Now $U_i$ is a subspace, so it's closed under vector addition. Hence, $x + y \in U_i$ . Since this is true for all $i \in I$ , I have $x + y \in \displaystyle \bigcap_{i \in I} U_i$ .

Thus, $\displaystyle \bigcap_{i \in I} U_i$ is closed under vector addition.

Next, suppose $k \in F$ and $x \in \displaystyle \bigcap_{i \in I} U_i$ . For x to be in the intersection of the $U_i$ , it must be in each $U_i$ for all $i \in I$ . So pick a particular $i \in I$ ; we have $x \in U_i$ . Now $U_i$ is a subspace, so it's closed under scalar multiplication. Hence, $k x \in U_i$ . Since this is true for all $i \in I$ , I have $k x \in \displaystyle \bigcap_{i \in I} U_i$ .

Thus, $\displaystyle \bigcap_{i \in I} U_i$ is closed under scalar multiplication.

Hence, $\displaystyle \bigcap_{i \in I} U_i$ is a subspace of V.

You can see that the proof was pretty easy, the two parts being pretty similar. The key idea is that something is in the intersection of a bunch of sets if and only if it's in each of the sets. How many sets there are in the bunch doesn't matter. If you're still feeling a little uncomfortable, try writing out the proof for the case of two subspaces: If U and V are subspaces of a vector space W over a field F, then $U \cap V$ is a subspace of W. The notation is easier for two subspaces, but the idea of the proof is the same as the idea for the proof above.

Contact information

Bruce Ikenaga's Home Page

Copyright 2022 by Bruce Ikenaga