Coordinate Transformations

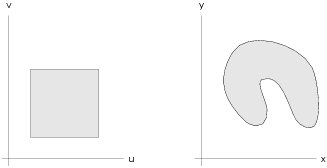
A coordinate transformation of the plane is a function $f:\real^2 \to \real^2$ . I'll usually assume that f has continuous partial derivatives, and that f is "essentially" one-to-one in the region of interest. (A function is one-to-one if different inputs produce different outputs.)

A coordinate transformation will usually be given by an equation . You can think of it as deforming or moving things in the u-v plane and placing them in the x-y plane.

$\hbox{\epsfysize=1.5in \epsffile{transform1.eps} \hskip0.5in \epsfysize=1.5in \epsffile{transform2.eps}}$

I'm going to look at some important special cases.

1. Linear transformations. You know that a linear transformation $\real^2 \to \real^2$ has the form

$\left[\matrix{x \cr y \cr}\right] = \left[\matrix{a & b \cr c & d \cr}\right] \left[\matrix{u \cr v \cr}\right].$

a, b, c, and d are numbers. In equation form, this is

$x = au + bv, \quad y = cu + dv.$

"Linear transformation" is long to write and say, so I'll often use linear map for short.

Linear maps always leave the origin fixed, since , gives , . (This is another way of saying that linear maps take the zero vector to the zero vector.) And as you might expect, linear maps carry lines to lines.

Moreover, a linear map takes squares to parallelograms:

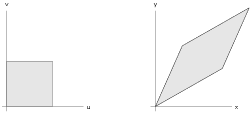
$\hbox{\epsfysize=1in \epsffile{transform3.eps} \hskip0.5in \epsfysize=1in \epsffile{transform4.eps}}$

For example, look at what happens to the unit square $0 \le u \le 1$ , $0 \le v \le 1$ :

$\left[\matrix{a & b \cr c & d \cr}\right] \left[\matrix{1 \cr 0 \cr}\right] = \left[\matrix{a \cr c \cr}\right]$

$\left[\matrix{a & b \cr c & d \cr}\right] \left[\matrix{0 \cr 1 \cr}\right] = \left[\matrix{b \cr d \cr}\right]$

The vectors $\langle 1, 0\rangle$ , $\langle 0, 1\rangle$ determine the unit square. They are mapped to the vectors $\langle a,c\rangle$ , $\langle b,d\rangle$ , two adjacent sides of the parallelogram.

$\hbox{\epsfysize=1.25in \epsffile{transform5.eps}}$

2. Translations. A translation $\real^2 \to \real^2$ has the form

$\left[\matrix{x \cr y \cr}\right] = \left[\matrix{u \cr v \cr}\right] + \left[\matrix{e \cr f \cr}\right].$

e and f are numbers. This translation just translates everything by the vector $\langle e,f\rangle$ .

$\hbox{\epsfysize=1.5in \epsffile{transform6.eps}}$

A translation by a nonzero vector is not a linear map, because linear maps must send the zero vector to the zero vector. However, translations are very useful in performing coordinate transformations. I'll introduce the following terminology for the composite of a linear transformation and a translation.

Definition. Let A be a real $m \times n$ matrix. An affine map is a function $f: \real^n \to \real^m$ of the form

$f(x) = Ax + b, \quad\hbox{where}\quad x \in \real^n \quad\hbox{and}\quad b \in \real^m.$

Example. Find an affine map which carries the unit square $0 \le u \le 1$ , $0 \le v \le 1$ to the parallelogram in the x-y plane with vertices , , , .

I'm going to make a rough sketch of the parallelogram first. I want to know the orientation of the vertices --- e.g. that B and C are next to A, and that D is opposite A.

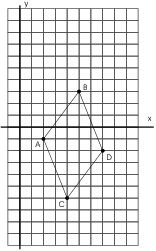
$\hbox{\epsfysize=2.25in \epsffile{transform7.eps}}$

I'm going to do the transformation in two steps. First, I'll take the square to a parallelogram which is the right size and shape, but which has a corner at the origin. Next, I'll move the parallelogram so it's at the right place.

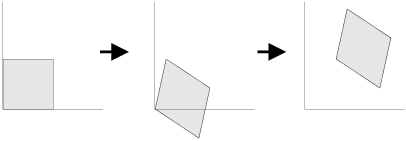
$\hbox{\epsfysize=1.25in \epsffile{transform8.eps}}$

The vectors from A to B and to C are $\bvec{AB} = \langle 3,4\rangle$ and $\bvec{AC} = \langle 2,-5\rangle$ . I saw above that if I construct a matrix with $\langle 3,4\rangle$ as the first column and $\langle 2,-5\rangle$ as the second column, then it will multiply $\langle 1,0\rangle$ to $\langle 3,4\rangle$ and $\langle 0,1\rangle$ to $\langle 2,-5\rangle$ :

$\left[\matrix{3 & 2 \cr 4 & -5 \cr}\right] \left[\matrix{1 \cr 0 \cr}\right] = \left[\matrix{3 \cr 4 \cr}\right] \qquad \left[\matrix{3 & 2 \cr 4 & -5 \cr}\right] \left[\matrix{0 \cr 1 \cr}\right] = \left[\matrix{2 \cr -5 \cr}\right]$

So the following transformation takes the unit square to a parallelogram of the right shape:

$\left[\matrix{x \cr y \cr}\right] = \left[\matrix{3 & 2 \cr 4 & -5 \cr}\right] \left[\matrix{u \cr v \cr}\right].$

This transformation takes to ; I want to go to the point A (which I used as the base point for my two vectors). To fix this, just translate by A:

$\left[\matrix{x \cr y \cr}\right] = \left[\matrix{3 & 2 \cr 4 & -5 \cr}\right] \left[\matrix{u \cr v \cr}\right] + \left[\matrix{2 \cr -1 \cr}\right].\quad\halmos$

3. Rotations. A rotation counterclockwise through an angle $\theta$ is given by

$\left[\matrix{x \cr y \cr}\right] = \left[\matrix{\cos \theta & -\sin \theta \cr \sin \theta & \cos \theta \cr}\right] \left[\matrix{u \cr v \cr}\right].$

To see this, just check that the unit vectors $\langle 1,0\rangle$ , $\langle 0,1\rangle$ go to the right places:

$\left[\matrix{\cos \theta & -\sin \theta \cr \sin \theta & \cos \theta \cr}\right] \left[\matrix{1 \cr 0 \cr}\right] = \left[\matrix{\cos \theta \cr \sin \theta \cr}\right] \qquad \left[\matrix{\cos \theta & -\sin \theta \cr \sin \theta & \cos \theta \cr}\right] \left[\matrix{0 \cr 1 \cr}\right] = \left[\matrix{-\sin \theta \cr \cos \theta \cr}\right]$

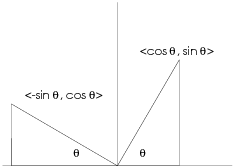
$\hbox{\epsfysize=1.5in \epsffile{transform9.eps}}$

You can see from the picture that $\langle 1,0\rangle$ and $\langle 0,1\rangle$ have both been rotated by an angle $\theta$ . Other vectors can be built out of these two vectors, so other vectors are rotated by $\theta$ as well.

4. Reflections. This is how to do a reflection across the x-axis:

$\left[\matrix{x \cr y \cr}\right] = \left[\matrix{1 & 0 \cr 0 & -1 \cr}\right] \left[\matrix{u \cr v \cr}\right] = \left[\matrix{u \cr -v \cr}\right].$

It is clear that this reflects things across the x-axis, because it simply negates the second component.

$\hbox{\epsfysize=1.5in \epsffile{transform10.eps}}$

What about reflection across a line L making an angle $\theta$ with the origin? It's messy to do using analytic geometry, but very easy using matrices. Simply do a rotation through $-\theta$ which carries L to the . Next, reflect across the x-axis. Finally, do a rotation through $-\theta$ which carries the x-axis back to L. Each of these transformations can be accomplished by matrix multiplication; just multiply the three matrices to do reflection across L.

Translations, rotations, and reflections are examples of rigid motions. They preserve distances between points, as well as areas.

Example. Find a real $2 \times 2$ matrix A such that

$f\left(\left[\matrix{x \cr y \cr}\right]\right) = A\left[\matrix{x \cr y \cr}\right]$

reflects points across the line $y = \sqrt{3}\,x$ .

The line $y = \sqrt{3}\,x$ makes an angle of $\dfrac{\pi}{3}$ with the positive x-axis. I can accomplish this transformation as follows:

$\hbox{\epsfysize=2in \epsffile{transform11.eps}}$

Thus,

$A = \left[\matrix{\cos \dfrac{\pi}{3} & -\sin \dfrac{\pi}{3} \cr \noalign{\vskip2pt} \sin \dfrac{\pi}{3} & \cos \dfrac{\pi}{3} \cr}\right] \left[\matrix{1 & 0 \cr 0 & -1 \cr}\right] \left[\matrix{\cos \dfrac{\pi}{3} & \sin \dfrac{\pi}{3} \cr \noalign{\vskip2pt} -\sin \dfrac{\pi}{3} & \cos \dfrac{\pi}{3} \cr}\right] = \left[\matrix{-\dfrac{1}{2} & \dfrac{\sqrt{3}}{2} \cr \noalign{\vskip2pt} \dfrac{\sqrt{3}}{2} & \dfrac{1}{2} \cr}\right].\quad\halmos$

Contact information

Bruce Ikenaga's Home Page