Vector Spaces

Vector spaces and linear transformations are the primary objects of study in linear algebra. A vector space (which I'll define below) consists of two sets: A set of objects called vectors and a field (the scalars).

You may have seen vectors before --- in physics or engineering courses, or in multivariable calculus. In those courses, you tend to see particular kinds of vectors, and it could lead you to think that those particular kinds of vectors are the only kinds of vectors. We'll discuss vectors by giving axioms for vectors. When you define a mathematical object using a set of axioms, you are describing how it behaves. Why is this important?

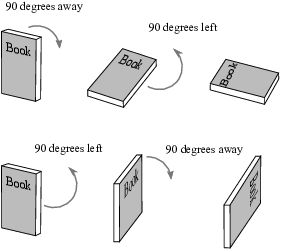
One common intuitive description of vectors is that they're things which "have a magnitude and a direction". This isn't a bad description for certain kinds of vectors, but it has some shortcomings. Consider the following example: Take a book and hold it out in front of you with the cover facing toward you.

$$\hbox{\epsfysize=2.25in \epsffile{vector-spaces-0.eps}}$$

First, rotate the book $90^{\circ}$ away from you, then (without returning the book to its original position) rotate the book $90^{\circ}$ to your left. The first three pictures illustrate the result.

Next, return the book to its original position facing you. Rotate the book $90^{\circ}$ to your left, then (without returning the book to its original position) rotate the book (without returning the book to its original position) away from you. The next three pictures illustrate the result.

In other words, we're doing two rotations --- $90^{\circ}$ away from you and $90^{\circ}$ to your left --- one after the other, in the two possible orders. Note that the final positions are different.

It's certainly reasonable to say that rotations by $90^{\circ}$ away from you or to your left are things with "magnitudes" and "directions". And it seems reasonable to "add" such rotations by doing one followed by the other. However, we saw that when we performed the "addition" in different orders, we got different results. Symbolically,

$$A + B \ne B + A.$$

The addition fails to be commutative. But it happens that we really do want vector addition to be commutative, for all of the "vectors" that come up in practice.

It is not enough to tell what a thing "looks like" ("magnitude and direction"); we need to say how the thing behaves. This example also showed that words like "magnitude" and "direction" are ambiguous.

Other descriptions of vectors --- as "arrow", or as "lists of numbers" --- also describe particular kinds of vectors. And as with "magnitude and direction", they're incomplete: They don't tell how the "vectors" in question behave.

Our axioms for a vector space describe how vectors should behave --- and if they behave right, we don't care what they look like! It's okay to think of "magnitude and direction" or "arrow" or "list of numbers", as long as you remember that these are only particular kinds of vectors.

Let's see the axioms for a vector space.

Definition. A vector space V over a field F is a set V equipped with two operations. The first is called (vector) addition; it takes vectors u and v and produces another vector $u + v$ .

The second operation is called scalar multiplication; it takes an element $a \in F$ and a vector $u \in V$ and produces a vector $au \in V$ .

These operations satisfy the following axioms:

1. Vector addition is associative: If $u, v, w \in V$ , then

$$(u + v) + w = u + (v + w).$$

2. Vector addition is commutative: If $u, v \in V$ , then

$$u + v = v + u.$$

3. There is a zero vector 0 which satisfies

$$0 + u = u = u + 0 \quad\hbox{for all}\quad u \in V.$$

Note: Some people prefer to write something like "$\vec{0}$ " for the zero vector to distinguish it from the number 0 in the field F. I'll be a little lazy and just write "0" and rely on you to determine whether it's the zero vector or the number zero from the context.

4. For every vector $u \in V$ , there is a vector $-u \in V$ which satisfies

$$u + (-u) = 0 = (-u) + u.$$

5. If $a, b \in F$ and $x \in V$ , then

$$a(b x) = (a b)x.$$

6. If $a, b \in F$ and $x \in V$ , then

$$(a + b)x = a x + b x.$$

7. If $a \in F$ and $x, y \in V$ , then

$$a(x + y) = a x + a y.$$

8. If $x \in V$ , then

$$1 \cdot x = x.$$

The elements of V are called vectors; the elements of F are called scalars. As usual, the use of words like "multiplication" does not imply that the operations involved look like ordinary "multiplication".

Note that Axiom (4) allows us to define subtraction of vectors this way:

$$x - y = x + (-y).$$

An easy (and trivial) vector space (over any field F) is the zero vector space $V = \{0\}$ . It consists of a zero vector (which is required by Axiom 3) and nothing else. The scalar multiplication is $a \cdot 0 = 0$ for any $a \in F$ . You can easily check that all the axioms hold.

The most important example of a vector space over a field F is given by the "standard" vector space $F^n$ . In fact, every (finite-dimensional) vector space over F is isomorphic to $F^n$ for some nonnegative integer n. We'll discuss isomorphisms later; let's give the definition of $F^n$ .

If F is a field and $n \ge 1$ , then $F^n$ denotes the set

$$F^n = \{(a_1, \ldots, a_n) \mid a_1, \ldots, a_n \in F\}.$$

If you know about (Cartesian) products, you can see that $F^n$ is the product of n copies of F.

We can also define $F^0$ to be the zero vector space $\{0\}$ .

If $v \in F^n$ and $v = (v_1, v_2, \ldots v_n)$ , I'll often refer to $v_1$ , $v_2$ , ... $v_n$ as the components of v.

Proposition. $F^n$ becomes a vector space over F with the following operations:

$$(a_1, \ldots, a_n) + (b_1, \ldots, b_n) = (a_1 + b_1, \ldots, a_n + b_n).$$

$$p \cdot (a_1, \ldots, a_n) = (p a_1, \ldots, p a_n), \quad\hbox{where}\quad p \in F.$$

$F^n$ is called the vector space of n-dimensional vectors over F. The elements $a_1$ , ..., $a_n$ are called the vector's components.

Proof. I'll check a few of the axioms by way of example.

To check Axiom 2, take $u, v \in F^n$ and write

$$u = (u_1, u_2, \ldots u_n) \quad\hbox{and}\quad v = (v_1, v_2, \ldots v_n).$$

Thus, $u_i, v_i \in F$ for $i = 1, \ldots n$ .

Then

$$u + v = (u_1, u_2, \ldots u_n) + (v_1, v_2, \ldots v_n) = (u_1 + v_1, u_2 + v_2, \ldots u_n + v_n) = (v_1 + u_1, v_2 + u_2, \ldots v_n + u_n) =$$

$$(v_1, v_2, \ldots v_n) +(u_1, u_2, \ldots u_n) = v + u.$$

The second equality used the fact that $u_i + v_i = v_i + u_i$ for each i, because the u's and v's are elements of the field F, and addition in F is commutative.

The zero vector is $0 = (0, 0, \ldots 0)$ (n components). I'll use "0" to denote the zero vector as well as the number 0 in the field F; the context should make it clear which of the two is intended. For instance, if v is a vector and I write "$0 + v$ ", the "0" must be the zero vector, since adding the number 0 to the vector v is not defined.

If $u = (u_1, u_2, \ldots u_n) \in F^n$ , then

$$0 + u = (0, 0, \ldots 0) + (u_1, u_2, \ldots u_n) = (0 + u_1, 0 + u_2, \ldots 0 + u_n) = (u_1, u_2, \ldots u_n) = u.$$

Since I already showed that addition of vectors is commutative, it follows that $u + 0 = 0$ as well. This verifies Axiom 3.

If $u = (u_1, u_2, \ldots u_n) \in F^n$ , then I'll define $-u = (-u_1, -u_2, \ldots -u_n)$ . Then

$$u + (-u) = (u_1, u_2, \ldots u_n) + (-u_1, -u_2, \ldots -u_n) = (u_1 - u_1, u_2 - u_2, \ldots u_n - u_n) = (0, 0, \ldots 0) = 0.$$

Commutativity of addition gives $(-u) + u = 0$ as well, and this verifies Axiom 4.

I'll write out the proof Axiom 6 in a little more detail. Let $p, q \in F$ , and let $(a_1, \ldots, a_n) \in F^n$ . Then

$$\matrix{(p + q)(a_1, \ldots, a_n) & = & \left((p + q)a_1, \ldots, (p + q)a_n\right) & \hbox{Definition of scalar multiplication} \cr & = & \left(p a_1 + q a_1, \ldots, p a_n + q a_n\right) & \hbox{Field axiom: Distributivity} \cr & = & (p a_1, \ldots, p a_n) + (q a_1, \ldots, q a_n) & \hbox{Definition of vector additon} \cr & = & p(a_1, \ldots, a_n) + q(a_1, \ldots, a_n) & \hbox{Definition of scalar multiplication} \cr}$$

You can see that checking the axioms amounts to writing out the vectors in component form, applying the definitions of vector addition and scalar multiplication, and using the axioms for a field.

While all vector spaces "look like" $F^n$ (at least if "n" is allowed to be infinite --- the fancy word is "isomorphism"), you should not assume that a given vector space is $F^n$ , unless you're explicitly told that it is. We'll see examples (like $C[0, 1]$ below) where it's not easy to see why a given vector space "looks like" $F^n$ .

In discussing matrices, we've referred to a matrix with a single row as a row vector and a matrix with a single column as a column vector.

$$\matrix{ \left[\matrix{1 & 2 & 3 \cr}\right] & \left[\matrix{1 \cr 2 \cr 3 \cr}\right] \cr \noalign{\vskip2pt} \hbox{row vector} & \hbox{column vector} \cr}$$

The elements of $F^n$ are just ordered n-tuples, not matrices. In certain situations, we may "identify" a vector in $F^n$ with a row vector or a column vector in the obvious way:

$$(1, 2, 3) \leftrightarrow \left[\matrix{1 & 2 & 3 \cr}\right] \leftrightarrow \left[\matrix{1 \cr 2 \cr 3 \cr}\right]$$

(Very often, we'll use a column vector, for reasons we'll see later.) I will mention this identification explicitly if we're doing this, but for right now just think of $(1, 2, 3)$ as an ordered triple, not a matrix.

You may have seen examples of $F^n$ -vector spaces before.

For instance, $\real^3$ consists of 3-dimensional vectors with real components, like

$$(3, -2, \pi) \quad\hbox{or}\quad \left(\dfrac{1}{2}, 0, -1.234\right).$$

You're probably familiar with addition and scalar multiplication for these vectors:

$$(1, -2, 4) + (4, 5, 2) = (1 + 4, -2 + 5, 4 + 2) = (5, 3, 6).$$

$$7 \cdot (-2, 0, 3) = (7 \cdot (-2), 7 \cdot 0, 7 \cdot 3) = (-14, 0, 21).$$

Note: Some people write $(3, -2, \pi)$ as "$\langle 3, -2, \pi\rangle$ ", using angle brackets to distinguish vectors from points.

Recall that $\integer_3$ is the field $\{0, 1, 2\}$ , where the operations are addition and multiplication mod 3. Thus, $\integer_3^2$ consists of 2-dimensional vectors with components in $\integer_3$ . Since each of the two components can be any element in $\{0, 1, 2\}$ , there are $3 \cdot 3 = 9$ such vectors:

$$(0, 0), (0, 1), (0, 2), (1, 0), (1, 1), (1, 2), (2, 0), (2, 1), (2, 2).$$

Here are examples of vector addition and multiplication in $\integer_3^2$ :

$$(1, 2) + (1, 1) = (1 + 1, 2 + 1) = (2, 0).$$

$$2 \cdot (2, 1) = (2 \cdot 2, 2 \cdot 1) = (1, 2).$$

We can picture elements of $F^n$ as points in n-dimensional space. Let's look at $\real^2$ , since it's easy to draw the pictures. $\real^2$ is the x-y-plane, and elements of $\real^2$ are points in the plane:

$$\hbox{\epsfysize=2in \epsffile{vector-spaces-1.eps}}$$

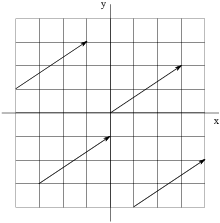
In the picture above, each grid square is $1 \times 1$ . The vectors $(2, 3)$ , $(2, -2)$ , $(-3, 0)$ , and $(-1, -4)$ are shown.

Vectors in $\real^n$ are often drawn as arrows going from the origin $(0, 0, \ldots, 0)$ to the corresponding point. Here's how the vectors in the previous picture look when represented with arrows:

$$\hbox{\epsfysize=2in \epsffile{vector-spaces-2.eps}}$$

If the x-component is negative, the arrow goes to the left; if the y-component is negative, the arrow goes down.

When you represent vectors in $\real^n$ as arrows, the arrows do not have to start at the origin. For instance, in $\real^2$ the vector $(3, 2)$ can be represented by any arrow which goes 3 units in the x-direction and 2 units in the y-direction, from the start of the arrow to the end of the arrow. All of the arrows in the picture below represent the vector $(3, 2)$ :

$$\hbox{\epsfysize=2in \epsffile{vector-spaces-3.eps}}$$

As long as the length and direction of the arrow don't change as it is moved around, it represents the same vector.

Representing vectors in $\real^n$ as arrows gives us a way of picturing vector addition, vector subtraction, and scalar multiplication.

To add vectors a and b represented as arrows, move one of the arrows --- say b --- so that it starts at the end of the vector a. As you move b, keep its length and direction the same:

$$\hbox{\epsfysize=1.15in \epsffile{vector-spaces-4.eps}}$$

As we noted earlier, if you don't change an arrow's length or direction, it represents the same vector. So the new vector is still b. The sum $a + b$ is represented by the arrow that goes from the start of a to the end of b.

You can also leave b alone and move a so it starts at the end of b. Then $b + a$ is the arrow going from the start of b to the end of a. Notice that it's the same as the arrow $a + b$ , which reflects the commutativity of vector addition: $a + b = b + a$ .

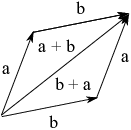
$$\hbox{\epsfysize=1.15in \epsffile{vector-spaces-5.eps}}$$

This picture also shows that you can think of $a + b$ (or $b + a$ ) as the arrow given by the diagonal of the parallelogram whose sides are a and b.

You can add more than two vectors in the same way. Move the vectors to make a chain, so that the next vector's arrow starts at the end of the previous vector's arrow. The sum is the arrow that goes from the start of the first arrow to the end of the last arrow:

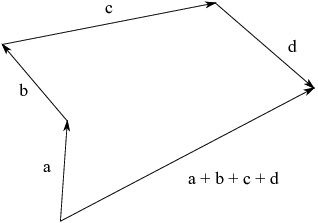
$$\hbox{\epsfysize=2in \epsffile{vector-spaces-6.eps}}$$

To subtract a vector b from a vector a --- that is, to do $a - b$ --- draw the arrow from the end of b to the end of a. This assumes that the arrows for a and b start at the same point:

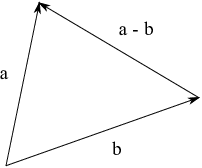
$$\hbox{\epsfysize=1.5in \epsffile{vector-spaces-7.eps}}$$

To see that this picture is correct, interpret it as an addition picture, where we're adding $a - b$ to b. The sum $(a - b) + b = a$ should be the arrow from the start of b to the end of $a - b$ , which it is.

When a vector a is multiplied by a real number k to get $k a$ , the arrow representing the vector is scaled up by a factor of k. In addition, if k is negative, the arrow is "flipped" $180^\circ$ , so it points in the opposite direction to the arrow for a.

$$\hbox{\epsfysize=1.75in \epsffile{vector-spaces-8.eps}}$$

In the picture above, the vector $2 a$ is twice as long as a and points in the same direction as a. The vector $-3 a$ is 3 times as long as a, but points in the opposite direction.

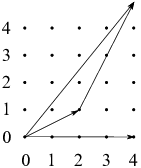
Example. Three vectors in $\real^2$ are shown in the picture below.

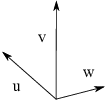
$$\hbox{\epsfysize=0.9in \epsffile{vector-spaces-9.eps}}$$

Draw the vector $u - 2 v + 3 w$ .

I start by constructing $2 v$ , an arrow twice as long as v in the same direction as v. I place it so it starts at the same place as u. Then the arrow that goes from the end of $2 v$ to the end of u is $u - 2 v$ .

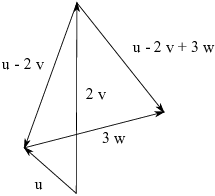
$$\hbox{\epsfysize=1.75in \epsffile{vector-spaces-10.eps}}$$

Next, I construct $3 w$ , an arrow 3 times as long as w in the same direction as w. I move $3 w$ so it starts at the end of $u - 2 v$ . Then the arrow from the start of $u - 2 v$ to the end of $3 w$ is $u - 2 v + 3 w$ .

While we can draw pictures of vectors when the field of scalars is the real numbers $\real$ , pictures don't work quite as well with other fields. As an example, suppose the field is $\integer_5 = \{0, 1, 2, 3, 4\}$ . Remember that the operations in $\integer_5$ are addition mod 5 and multiplication mod 5. So, for instance,

$$4 + 3 = 2 \quad\hbox{and}\quad 2 \cdot 4 = 3.$$

We saw that $\real^2$ is just the x-y plane. What about $\integer_5^2$ ? It consists of pairs $(a, b)$ where a and b are elements of $\integer_5$ . Since there are 5 choices for a and 5 choices for b, there are $5 \cdot 5 = 25$ elements in $\integer_5^2$ . We can picture it as a $5 \times 5$ grid of dots:

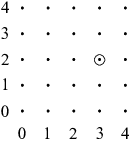
$$\hbox{\epsfysize=1.25in \epsffile{vector-spaces-11.eps}}$$

The dot corresponding to the vector $(3, 2)$ is circled as an example.

Picturing vectors as arrows seems to work until we try to do vector arithmetic. For example, suppose $v = (3, 4)$ in $\integer_5^2$ . We can represent it with an arrow from the origin to the point $(3, 4)$ .

Suppose we multiply v by 2. You can check that $2 v = (1, 3)$ .

Here's a picture showing $v = (3, 4)$ and $2 v = (1, 3)$ :

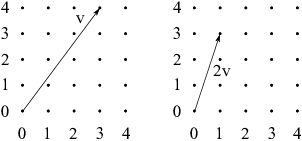
$$\hbox{\epsfysize=1.25in \epsffile{vector-spaces-12.eps}}$$

In $\real^2$ , we'd expect $2 v$ to have the same direction as v and twice the length. You can see that it doesn't work that way in $\integer_5^2$ .

What about vector addition in $\integer_5^2$ ? Suppose we add $(2, 1)$ and $(2, 4)$ :

$$(2, 1) + (2, 4) = (2 + 2, 1 + 4) = (4, 0).$$

If we represent the vectors as arrows and try to add the arrows as we did in $\real^2$ , we encounter problems. First, when I move $(2, 4)$ so that it starts at the end of $(2, 1)$ , the end of $(2, 4)$ sticks outside of the $5 \times 5$ grid which represents $\integer_5^2$ .

$$\hbox{\epsfysize=1.5in \epsffile{vector-spaces-13.eps}}$$

If I ignore this problem and I draw the arrow from the start of $(1, 2)$ to the end of $(2, 4)$ , the diagonal arrow which should represent the sum looks very different from the actual sum arrow $(4, 0)$ (the horizontal arrow in the picture) --- and as with $(2, 4)$ , the end of the sum arrow sticks outside the grid which represents $\integer_5^2$ .

You can see that thinking of vectors as arrows has limitations. It's okay for vectors in $\real^n$ .

What about thinking of vectors as "lists of numbers"? That seemed to work in the examples above in $\real^n$ and in $\integer_5^2$ . In general, this works for the $F^n$ vector spaces for finite n, but those aren't the only vector spaces.

Here are some examples of vector spaces which are not $F^n$ 's, at least for finite n.

The set $\real[x]$ of polynomials with real coefficients is a vector space over $\real$ , using the standard operations on polynomials. For example, you add polynomials and multiply them by numbers in the usual ways:

$$(2 x^2 + 3 x + 5) + (x^3 + 7 x - 11) = x^3 + 2 x^2 + 10 x - 6.$$

$$4 \cdot (-3 x^2 + 10) = -12 x^2 + 40.$$

Unlike $\real^n$ , the set of polynomials $\real[x]$ is infinite dimensional. (We'll discuss the dimension of a vector space more precisely later). Intuitively, you need an infinite set of polynomials, like $1, x, x^2, x^3, \ldots$ to "construct" all the elements of $\real[x]$ .

You might notice that we can represent polynomials as "lists of numbers", as long as we're willing to allow infinite lists. For example,

$$x^3 + 2 x^2 + 10 x - 6 = (-6, 10, 2, 1, 0, 0, \ldots), \quad\hbox{and}\quad -12 x^2 + 40 = (40, 0, -12, 0, 0, \ldots).$$

We have to begin with the lowest degree coefficient and work our way up, because polynomials can have arbitrarily large degree. So a polynomial whose highest power term was $3 x^{100}$ might have nonzero numbers from the zeroth slot up to the "3" in the $101^{\rm st}$ slot, followed by an infinite number of zeros.

Not bad! It's hard to see how we could think of these as "arrows", but at least we have something like our earlier examples.

However, sometimes you can't represent an element of a vector space as a "list of numbers", even if you allow an "infinite list".

Let $C([0, 1])$ denote the continuous real-valued functions defined on the interval $0 \le x \le 1$ . You add functions pointwise:

$$(f + g)(x) = f(x) + g(x) \quad\hbox{for}\quad f, g \in C([0, 1]).$$

From calculus, you know that the sum of continuous functions is a continuous function. For instance, if $f(x) = e^x$ and $g(x) = \sin (x^3 + 1)$ , then

$$f(x) + g(x) = e^x + \sin (x^3 + 1).$$

If $a \in \real$ and $f \in C([0, 1])$ , define scalar multiplication in pointwise fashion:

$$(a f)(x) = a \cdot f(x).$$

For example, if $f(x) = x^2$ and $a = 3$ , then

$$(a f)(x) = 3 x^2.$$

These operations make $C([0, 1])$ into an $\real$ -vector space.

$C([0, 1])$ is infinite dimensional just like $\real[x]$ . However, its dimension is uncountably infinite, while $\real[x]$ has countably infinite dimension over $\real$ . We can't represent elements of $C([0, 1])$ as a "list of numbers", even infinite lists of numbers.

Thinking of vectors as arrows or lists of numbers is fine where it's appropriate. But be aware that those ways of thinking about vectors don't apply in every case.

Having seen some examples, let's wind up by proving some easy properties of vectors in vector spaces. The next result says that many of the "obvious" things you'd assume about vector arithmetic are true.

Proposition. Let V be a vector space over a field F.

(a) $0 \cdot x = 0$ for all $x \in V$ .

Note: The "0" on the left is the number 0 in the field F, while the "0" on the right is the zero vector in V.

(b) $k \cdot 0 = 0$ for all $k \in F$ .

Note: On both the left and right, "0" denotes the zero vector in V.

(c) $(-1) \cdot x = -x$ for all $x \in V$ .

(d) $-(-x) = x$ for all $x \in V$ .

Proof. (a) As I noted above, the "0" on the left is the zero in F, whereas the "0" on the right is the zero vector in V. We use a little trick, writing 0 as $0 + 0$ :

$$0 \cdot x = (0 + 0) \cdot x = 0 \cdot x + 0 \cdot x.$$

The first step used the definition of the number zero: "Zero plus anything gives the anything", so take the "anything" to be the number 0 itself. The second step used distributivity.

Next, I'll subtract $0 \cdot x$ from both sides. Just this once, I'll show all the steps using the axioms. Start with the equation above, and add $-(0 \cdot x)$ to both sides:

$$\matrix{ 0 \cdot x = 0 \cdot x + 0 \cdot x & \cr 0 \cdot x + [-(0 \cdot x)] = (0 \cdot x + 0 \cdot x) + [-(0 \cdot x)] & \cr 0 = (0 \cdot x + 0 \cdot x) + [-(0 \cdot x)] & (\hbox{Axiom (4)}) \cr 0 = 0 \cdot x + (0 \cdot x + [-(0 \cdot x)]) & (\hbox{Axiom (1)}) \cr 0 = 0 \cdot x + 0 & (\hbox{Axiom (4)}) \cr 0 = 0 \cdot x & (\hbox{Axiom (3)}) \cr}$$

Normally, I would just say: "Subtracting $0 \cdot x$ from both sides, I get $0 = 0 \cdot x$ ." It's important to go through a few simple proofs based on axioms to ensure that you really can do them. But the result isn't very surprising: You'd expect "zero times anything to equal zero". In the future, I won't usually do elementary proofs like this one in such detail.

(b) Note that "0" on both the left and right denotes the zero vector, not the number 0 in F. I use the same idea as in the proof of (a):

$$k \cdot 0 = k \cdot (0 + 0) = k \cdot 0 + k \cdot 0.$$

The first step used the definition of the zero vector, and the second used distributivity. Now subtract $k \cdot 0$ from both sides to get $0 = k \cdot 0$ .

(c) (The "-1" on the left is the scalar -1; the "$-x$ " on the right is the "negative" of $x \in V$ .)

$$(-1) \cdot x + x = (-1) \cdot x + 1 \cdot x = \left((-1) + 1\right) \cdot x = 0 \cdot x = 0.$$

(d)

$$-(-x) = (-1) \cdot [(-1) \cdot x] = [(-1) \cdot (-1)]x = 1 \cdot x = x.\quad\halmos$$

Contact information

Bruce Ikenaga's Home Page

Copyright 2022 by Bruce Ikenaga