The Fermat-Pell Equation

Consider a Diophantine equation of the form

$$x^2 - d y^2 = n.$$

If d is a perfect square, you can solve the equation directly.

Example. Solve the Diophantine equation $x^2 - 9 y^2 = 13$ .

What about the equation $x^2 - 9 y^2 = 10$ ?

I can write the equation as

$$(x - 3 y)(x + 3 y) = 13.$$

This is an equation in integers, and represents a factorization of 13. There are only two ways to factor 13 in positive integers: $1 \cdot 13$ and $13 \cdot 1$ . (You can check that the negative factorizations give the same results.)

Suppose $x - 3 y = 1$ and $x + 3y = 13$ . This is

$$\matrix{ x & - & 3 y & = & 1 \cr x & + & 3 y & = & 13 \cr} \quad\hbox{or}\quad \left[\matrix{ 1 & -3 \cr 1 & 3 \cr}\right] \left[\matrix{x \cr y \cr}\right] = \left[\matrix{1 \cr 13 \cr}\right].$$

So

$$\left[\matrix{x \cr y \cr}\right] = \dfrac{1}{6} \left[\matrix{ 3 & 3 \cr -1 & 1 \cr}\right] \left[\matrix{1 \cr 13 \cr}\right] = \left[\matrix{7 \cr 2 \cr}\right].$$

$(x, y) = (7, 2)$ is an integer solution, so it qualifies as a solution to the original equation. Since x and y appear as $x^2$ and $y^2$ in the original equation, $(-7, 2)$ , $(7, -2)$ , and $(-7, -2)$ also work.

Similarly, $x - 3 y = 13$ and $x + 3 y = 1$ give $(x, y) = (-7, 2)$ (which I already know).

So the solutions to the Diophantine equation $x^2 - 9 y^2 = 13$ are $(7, 2)$ , $(-7, 2)$ , $(7, -2)$ , and $(-7, -2)$ .

Now suppose I change the problem to $x^2 - 9 y^2 = 10$ . Write it as

$$(x - 3 y)(x + 3 y) = 10.$$

The possible factorizations of 10 are $1 \cdot 10$ , $10 \cdot 1$ , $2 \cdot 5$ , and $5 \cdot 2$ .

Try $x - 3 y = 1$ , $x + 3 y = 10$ . Then

$$\left[\matrix{ 1 & -3 \cr 1 & 3 \cr}\right] \left[\matrix{x \cr y \cr}\right] = \left[\matrix{1 \cr 10 \cr}\right], \quad\hbox{so}\quad \left[\matrix{x \cr y \cr}\right] = \dfrac{1}{6} \left[\matrix{ 3 & 3 \cr -1 & 1 \cr}\right] \left[\matrix{1 \cr 10 \cr}\right] = \left[\matrix{\dfrac{11}{2} \cr \noalign{\vskip2pt} \dfrac{3}{2} \cr}\right].$$

This is not a solution in integers, so this factorization gives no integer solutions.

You can verify that the other factorizations do not give integer solutions. Hence, $x^2 - 9 y^2 = 10$ has no integer solutions.

Now consider the case where d is not a perfect square. The following facts (which I'll state without proof) relate the solutions to $x^2 - d y^2 = n$ to the continued fraction expansion of $\sqrt{d}$ .

Theorem. Suppose $d > 0$ , d is not a perfect square, and $|k| < \sqrt{d}$ . Any positive solution of $x^2 - d y^2 = k$ with $(x, y) = 1$ satisfies $x = p_n$ , $y = q_n$ for some $n > 0$ , where $\dfrac{p_n}{q_n}$ is the n-th convergent of the continued fraction expansion of $\sqrt{d}$ .

The theorem doesn't say which convergent will give a solution. The special form $x^2 - d y^2 = \pm 1$ is called the Fermat-Pell equation. In this case, it's possible to say which convergent will solve the equation. I'll state the following facts without proof, and give some examples.

First, recall from the theory of periodic continued fractions that a quadratic irrational --- in particular, a number of the form $\sqrt{d}$ , where d is not a square --- has a periodic continued fraction expansion.

Theorem. If $d > 0$ and d is not a perfect square, then the continued fraction expansion of $\sqrt{d}$ is periodic, and has the form

$$[a_0, \overline{a_1, \ldots, a_{n - 1}, 2 a_0}].\quad\halmos$$

Theorem. Suppose $d > 0$ and d is not a perfect square. Any positive solution of $x^2 - d y^2 = \pm 1$ with $(x, y) = 1$ satisfies $x = p_n$ , $y = q_n$ for some $n > 0$ , where $\dfrac{p_n}{q_n}$ is the n-th convergent of the continued fraction expansion of $\sqrt{d}$ .

Let t be the period of the expansion of $\sqrt{d}$ .

(a) If t is even, then $x^2 - d y^2 = -1$ has no solutions. $x^2 - d y^2 = 1$ has solutions $x = p_{n t - 1}$ , $y = q_{n t - 1}$ for $n \ge 1$ .

(b) If t is odd, then $x^2 - d y^2 = -1$ has solutions $x = p_{n t - 1}$ , $y = q_{n t - 1}$ for $n = 1, 3, 5, \ldots$ , and $x^2 - d y^2 = 1$ has solutions $x = p_{n t - 1}$ , $y = q_{n t - 1}$ for $n = 2, 4, 6, \ldots$ .

Example. (a) Find the first 6 terms ($a_0$ through $a_5$ ) and the numerators and denominators of the first 6 convergents ($p_0$ , $q_0$ through $p_5$ , $q_5$ ) of the continued fraction expansion of $\sqrt{14}$ .

(b) Use the continued fraction for $\sqrt{14}$ to find solutions to the Fermat-Pell equations

$$x^2 - 14 y^2 = -1 \quad\hbox{and}\quad x^2 - 14 y^2 = 1.$$

(a)

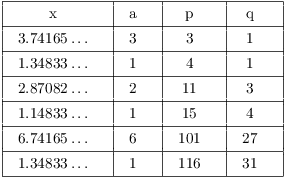
$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & \cr & x & & a & & p & & q & \cr height2pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & \cr & $3.74165 \ldots$ & & 3 & & 3 & & 1 & \cr height2pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & \cr & $1.34833 \ldots$ & & 1 & & 4 & & 1 & \cr height2pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & \cr & $2.87082 \ldots$ & & 2 & & 11 & & 3 & \cr height2pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & \cr & $1.14833 \ldots$ & & 1 & & 15 & & 4 & \cr height2pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & \cr & $6.74165 \ldots$ & & 6 & & 101 & & 27 & \cr height2pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & \cr & $1.34833 \ldots$ & & 1 & & 116 & & 31 & \cr height2pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} }} $$

(b) The expansion has period 4, which is even. Hence, $x^2 - 14 y^2 = -1$ has no solutions.

The first solution to $x^2 -14 y^2 = 1$ is $(p_{4 - 1}, q_{4 - 1}) = (p_3, q_3) = (15, 4)$ . You can check that

$$15^2 - 14 \cdot 4^2 = 1.\quad\halmos$$

Example. (a) Find the first 6 terms ($a_0$ through $a_5$ ) and the numerators and denominators of the first 6 convergents ($p_0$ , $q_0$ through $p_5$ , $q_5$ ) of the continued fraction expansion of $\sqrt{41}$ .

(b) Use the continued fraction for $\sqrt{41}$ to find solutions to the Fermat-Pell equations

$$x^2 - 41 y^2 = -1 \quad\hbox{and}\quad x^2 - 41 y^2 = 1.$$

(a)

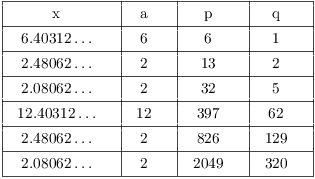
$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & \cr & x & & a & & p & & q & \cr height2pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & \cr & $6.40312 \ldots$ & & 6 & & 6 & & 1 & \cr height2pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & \cr & $2.48062 \ldots$ & & 2 & & 13 & & 2 & \cr height2pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & \cr & $2.08062 \ldots$ & & 2 & & 32 & & 5 & \cr height2pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & \cr & $12.40312 \ldots$ & & 12 & & 397 & & 62 & \cr height2pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & \cr & $2.48062 \ldots$ & & 2 & & 826 & & 129 & \cr height2pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & \cr & $2.08062 \ldots$ & & 2 & & 2049 & & 320 & \cr height2pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} }} $$

(b) The period is 3, which is odd. The first solution to $x^2 - 41 y^2 = -1$ is given by $(p_{3 - 1}, q_{3 - 1}) = (p_2, q_2) = (32, 5)$ . You can check that

$$32^2 - 41 \cdot 5^2 = -1.$$

For $x^2 - 41 y^2 = 1$ , I have $2 \cdot 3 - 1 = 5$ , so the first solution is given by $(p_5, q_5) = (2049, 320)$ . You can check that

$$2049^2 - 41 \cdot 320^2 = 1.\quad\halmos$$

In fact, you can generate the solution to the second equation using the solution to the first. Take $(32, 5)$ , and compute

$$(32 - 5 \sqrt{41})^2 = 2049 + 320 \sqrt{41}.$$

The coefficients $(2049, 320)$ give the solution to the second equation.

Here's an interesting example. The continued fraction expansion of $\sqrt{1141}$ is

$$[33, 1, 3, 1, 1, 12, 1, 21, 1, 1, 2, 5, 4, 3, 7, 5, 16, 1, 2, 3, 1, 1, 1, 2, 1, 2, 1, 4, 1, 8, 1, 4, 1,$$

$$\hskip0.5in 2, 1, 2, 1, 1, 1, 3, 2, 1, 16, 5, 7, 3, 4, 5, 2, 1, 1, 21, 1, 12, 1, 1, 3, 1, 66, \ldots]$$

It repeats after that.

The period is $t = 58$ , so $x^2 - 1141 y^2 = 1$ has solutions of the form $p_{58 n - 1}$ , $q_{58 n - 1}$ . Here's one:

$$x = 1036782394157223963237125215, \quad y = 30693385322765657197397208.$$

Contact information

Bruce Ikenaga's Home Page

Copyright 2024 by Bruce Ikenaga