Finite Continued Fractions

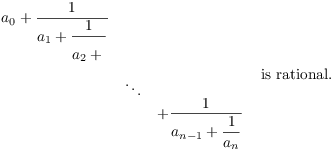
Definition. Let $a_0$ , ... $a_n$ be real numbers, with $a_1$ , ..., $a_n$ positive. A finite continued fraction is an expression of the form

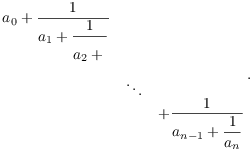
$$\matrix{a_0 + \dfrac{1}{a_1 + \dfrac{1}{a_2 + \vphantom{\dfrac{1}{a_3}}}} & & \cr & \ddots & \cr & & + \dfrac{1}{a_{n - 1} + \dfrac{1}{a_n}} \cr}.$$

To make the writing easier, I'll denote the continued fraction above by $[a_0; a_1, a_2, \ldots, a_n]$ . In most cases, the $a_i$ 's will be integers.

Remark. In some cases people have considered continued fractions where the numerators don't have to be 1. For example,

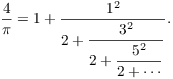
$$\dfrac{4}{\pi} = 1 + \dfrac{1^2}{2 + \dfrac{3^2}{2 + \dfrac{5^2}{2 + \cdots}}}.$$

In this case, they refer to continued fractions where the numerators are all 1 as simple continued fractions.

I will only be considering continued fractions where the numerators are all 1. So to save writing, I won't use the adjective "simple", and use the phrase "continued fraction" to mean a continued fraction with numerators all eqaul to 1.

Example. Find a continued fraction expansion for $\dfrac{47}{17}$ .

I can do this by repeated division:

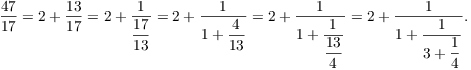
$$\dfrac{47}{17} = 2 + \dfrac{13}{17} = 2 + \dfrac{1}{\dfrac{17}{13}} = 2 + \dfrac{1}{1 + \dfrac{4}{13}} = 2 + \dfrac{1}{1 + \dfrac{1}{\dfrac{13}{4}}} = 2 + \dfrac{1}{1 + \dfrac{1}{3 + \dfrac{1}{4}}}.$$

In short form, $\dfrac{47}{17} = [2; 1, 3, 4]$ .

Now repeated division is what you do in executing the Euclidean algorithm and so a little bit of thought should convince you that you can express any rational number as a finite continued fraction in this way. Specifically,

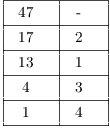
$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2pt & \omit & & \omit & \cr & 47 & & - & \cr height2pt & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & \cr & 17 & & 2 & \cr height2pt & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & \cr & 13 & & 1 & \cr height2pt & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & \cr & 4 & & 3 & \cr height2pt & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & \cr & 1 & & 4 & \cr height2pt & \omit & & \omit & \cr \noalign{\hrule} }} $$

Notice that the successive quotients 2, 1, 3, and 4 are the numbers in the continued fraction expansion.

Example. Find a finite continued fraction expansion for $\dfrac{117}{17}$ .

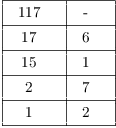
$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2pt & \omit & & \omit & \cr & 117 & & - & \cr height2pt & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & \cr & 17 & & 6 & \cr height2pt & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & \cr & 15 & & 1 & \cr height2pt & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & \cr & 2 & & 7 & \cr height2pt & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & \cr & 1 & & 2 & \cr height2pt & \omit & & \omit & \cr \noalign{\hrule} }} $$

$$\dfrac{117}{17} = [6; 1, 7, 2] = 6 + \dfrac{1}{1 + \dfrac{1}{7 + \dfrac{1}{2}}}.\quad\halmos$$

I have been asking for a finite continued fraction expansion, not the finite continued fraction expansion. In fact, the continued fraction expansion of a rational number is not unique. For example,

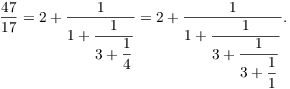
$$\dfrac{47}{17} = 2 + \dfrac{1}{1 + \dfrac{1}{3 + \dfrac{1}{4}}} = 2 + \dfrac{1}{1 + \dfrac{1}{3 + \dfrac{1}{3 + \dfrac{1}{1}}}}.$$

And in general,

$$[a_0; a_1, a_2, \ldots, a_{n - 1}, a_n] = [a_0; a_1, a_2, \ldots, a_{n - 1}, a_n - 1, 1].\quad\halmos$$

Lemma. Every finite continued fraction with integer terms represents a rational number.

Proof. If $a_0 \in \integer$ , then $[a_0]$ is rational.

Inductively, suppose that a finite continued fraction with $n - 1$ "levels" is a rational number. I want to show that

$$\matrix{a_0 + \dfrac{1}{a_1 + \dfrac{1}{a_2 + \vphantom{\dfrac{1}{a_3}}}} & & \cr & \ddots & \cr & & + \dfrac{1}{a_{n - 1} + \dfrac{1}{a_n}} \cr} \quad\hbox{is rational}.$$

By induction,

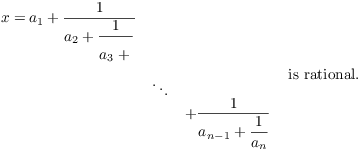
$$\raise0.52in\hbox{$x =$} \matrix{a_1 + \dfrac{1}{a_2 + \dfrac{1}{a_3 + \vphantom{\dfrac{1}{a_4}}}} & & \cr & \ddots & \cr & & + \dfrac{1}{a_{n - 1} + \dfrac{1}{a_n}} \cr} \quad\hbox{is rational}.$$

So

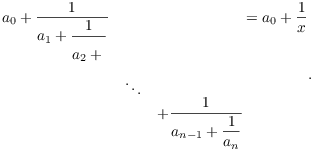
$$\matrix{a_0 + \dfrac{1}{a_1 + \dfrac{1}{a_2 + \vphantom{\dfrac{1}{a_3}}}} & & \cr & \ddots & \cr & & + \dfrac{1}{a_{n - 1} + \dfrac{1}{a_n}} \cr} \raise0.52in\hbox{$= a_0 + \dfrac{1}{x}$}.$$

This is the sum of two rational numbers, which is rational as well.

I'd like eventually to discuss infinite continued fractions --- things that look like

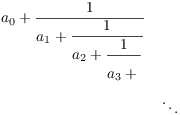
$$\matrix{a_0 + \dfrac{1}{a_1 + \dfrac{1}{a_2 + \dfrac{1}{a_3 + \vphantom{\dfrac{1}{a_4}}}}} & & \cr & \ddots & \cr}$$

In preparation for this, I'll look at the effect of truncating a continued fraction.

Definition. The $k^{\rm th}$ convergent of the continued fraction $[a_0; a_1, a_2, \ldots, a_n]$ is

$$c_k = [a_0; a_1, a_2, \ldots, a_k].$$

Note that for $k \ge n$ , $c_k = [a_0; a_1, a_2, \ldots, a_n]$ .

Example. Find the first four convergents of $[1; 2, 3, 2]$ .

$$c_0 = 1$$

$$c_1 = 1 + \dfrac{1}{2} = \dfrac{3}{2}$$

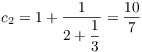
$$c_2 = 1 + \dfrac{1}{2 + \dfrac{1}{3}} = \dfrac{10}{7}$$

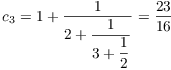
$$c_3 = 1 + \dfrac{1}{2 + \dfrac{1}{3 + \dfrac{1}{2}}} = \dfrac{23}{16}$$

And $c_4 = c_5 = \cdots = \dfrac{23}{16}$ as well.

It is tedious to have to compute convergents by doing the algebra to simplify an enormous fraction. The next result gives an algorithm for computing the convergents of a continued fraction. It's important for theoretical reasons, too --- I'll need it for several of the proofs that follow. For the theorem, I won't assume that the $a_i$ 's are integers, since I will need the general result later on.

Theorem. Let $a_0, a_1, \ldots \in \real$ , where $a_0 \ge 0$ and $a_1, \ldots a_n > 0$ . Let

$$p_0 = a_0, \quad q_0 = 1$$

$$p_1 = a_1 a_0 + 1, \quad q_1 = a_1$$

$$p_k = a_k p_{k - 1} + p_{k - 2}, \quad q_k = a_k q_{k - 1} + q_{k - 2} \quad\hbox{for}\quad k \ge 2.$$

Then the k-th convergent of $[a_0; a_1, a_2, \ldots, a_n]$ is $c_k = \dfrac{p_k}{q_k}$ .

Proof. First, note that

$$\raise0.61in\hbox{$[b_0; b_1, \ldots, b_k, b_{k + 1}] =$} \matrix{b_0 + \dfrac{1}{b_1 + \dfrac{1}{b_2 + \vphantom{\dfrac{1}{b_3}}}} & & \cr & \ddots & \cr & & + \dfrac{1}{b_{k - 1} + \dfrac{1}{b_k + \dfrac{1}{b_{k + 1}}}} \cr} \raise0.61in\hbox{$= \left[b_0; b_1, \ldots, b_k + \dfrac{1}{b_{k + 1}}\right]$}.$$

I got this by regarding the last two terms as a single term.

Note also that $p_0$ , ..., $p_{k - 1}$ and $q_0$ , ..., $q_{k - 1}$ are the same for these two fractions, since they only differ in the k-th term.

Now I'll start the proof --- it will go by induction on k. For $k = 0$ ,

$$c_0 = a_0 = \dfrac{a_0}{1} = \dfrac{p_0}{q_0}.$$

And for $k = 1$ ,

$$c_1 = a_0 + \dfrac{1}{a_1} = \dfrac{a_1a_0 + 1}{a_1} = \dfrac{p_1}{q_1}.$$

Suppose $k \ge 2$ , and assume that result holds through the k-th convergent. Then

$$c_{k + 1} = [a_0; a_1, \ldots, a_k, a_{k + 1}] = \left[a_0; a_1, \ldots, a_k + \dfrac{1}{a_{k + 1}}\right].$$

Now this is the k-th convergent of a continued fraction, so by induction this is $\dfrac{p_k}{q_k}$ , where $p_k$ and $q_k$ refer to $\left[a_0; a_1, \ldots, a_k + \dfrac{1}{a_{k + 1}}\right]$ (as opposed to $[a_0; a_1, \ldots, a_k, a_{k + 1}]$ ). But what are the $p_k$ and $q_k$ for this fraction? They're given inductively by

$$p_k = (k\hbox{-th term})p_{k - 1} + p_{k - 2}, \quad q_k = (k\hbox{-th term})q_{k - 1} + q_{k - 2}.$$

Now $p_{k - 2}$ , $p_{k - 1}$ , $q_{k - 2}$ , $q_{k - 1}$ are the same for $\left[a_0; a_1, \ldots, a_k + \dfrac{1}{a_{k + 1}}\right]$ and $[a_0; a_1, \ldots, a_k, a_{k + 1}]$ , as I noted at the start. On the other hand, the k-th term of $\left[a_0; a_1, \ldots, a_k + \dfrac{1}{a_{k + 1}}\right]$ is $a_k + \dfrac{1}{a_{k + 1}}$ . So

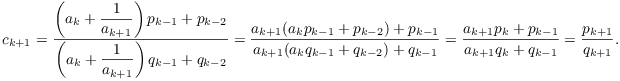
$$c_{k + 1} = \dfrac{\left(a_k + \dfrac{1}{a_{k + 1}}\right)p_{k - 1} + p_{k - 2}}{\left(a_k + \dfrac{1}{a_{k + 1}}\right)q_{k - 1} + q_{k - 2}} = \dfrac{a_{k + 1}(a_kp_{k - 1} + p_{k - 2}) + p_{k - 1}}{a_{k + 1}(a_kq_{k - 1} + q_{k - 2}) + q_{k - 1}} = \dfrac{a_{k + 1}p_k + p_{k - 1}}{a_{k + 1}q_k + q_{k - 1}} = \dfrac{p_{k + 1}}{q_{k + 1}}.$$

(The next to the last equality also follows by induction.) This shows that the result holds for $k + 1$ , so the induction step is complete.

Example. Compute $c_4$ for $[1; 2, 1, 2, 1]$ .

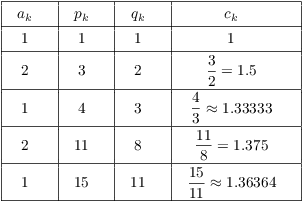
$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & \cr & $a_k$ & & $p_k$ & & $q_k$ & & $c_k$ & \cr height2pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & \cr & 1 & & 1 & & 1 & & 1 & \cr height2pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & \cr & 2 & & 3 & & 2 & & $\dfrac{3}{2} = 1.5$ & \cr height2pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & \cr & 1 & & 4 & & 3 & & $\dfrac{4}{3} \approx 1.33333$ & \cr height2pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & \cr & 2 & & 11 & & 8 & & $\dfrac{11}{8} = 1.375$ & \cr height2pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & \cr & 1 & & 15 & & 11 & & $\dfrac{15}{11} \approx 1.36364$ & \cr height2pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} }} $$

There is a pattern to the computation of the p's and q's which makes things pretty easy. To get the next p, for instance, multiply the current a by the last p and add the next-to-the-last p.

$$\hbox{\epsfysize=3in \epsffile{finite-continued-fractions-1.eps}}$$

Notice that in the last example, the convergents oscillate, and that the fractions which give the convergents are always in lowest terms. We'll see that this holds in general.

Example. Find $c_4$ for $[1; 1, 3, 1, 3]$ .

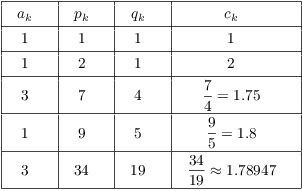
$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & \cr & $a_k$ & & $p_k$ & & $q_k$ & & $c_k$ & \cr height2pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & \cr & 1 & & 1 & & 1 & & 1 & \cr height2pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & \cr & 1 & & 2 & & 1 & & 2 & \cr height2pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & \cr & 3 & & 7 & & 4 & & $\dfrac{7}{4} = 1.75$ & \cr height2pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & \cr & 1 & & 9 & & 5 & & $\dfrac{9}{5} = 1.8$ & \cr height2pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & \cr & 3 & & 34 & & 19 & & $\dfrac{34}{19} \approx 1.78947$ & \cr height2pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} }} $$

Again, notice that the convergents oscillate, and that the fractions for the convergents are always in lowest terms.

I'll prove that the convergent fractions are in lowest terms first.

Theorem. Let $a_0, a_1, \ldots \in \real$ , where $a_0 \ge 0$ and $a_1, \ldots a_n > 0$ . Let

$$p_0 = a_0, \quad q_0 = 1$$

$$p_1 = a_1 a_0 + 1, \quad q_1 = a_1$$

$$p_k = a_k p_{k - 1} + p_{k - 2}, \quad q_k = a_k q_{k - 1} + q_{k - 2} \quad\hbox{for}\quad k \ge 2.$$

Then

$$p_k q_{k - 1} - p_{k - 1} q_k = (-1)^{k - 1} \quad\hbox{for}\quad k \ge 1.$$

Proof. I'll induct on k. For $k = 1$ ,

$$p_1 q_0 - p_0 q_1 = (a_1 a_0 + 1)(1) - (a_0)(a_1) = 1 = 1^{1-1}.$$

Take $k > 1$ , and assume the result holds for k. Then

$$p_{k + 1} q_k - p_k q_{k + 1} = (a_{k + 1} p_k + p_{k - 1}) q_k - p_k(a_{k + 1} q_k + q_{k - 1}) = p_{k - 1} q_k - p_k q_{k - 1} =$$

$$-\left(p_kq _{k - 1} - p_{k - 1} q_k = (-1)^{k - 1}\right) = -(-1)^{k - 1} = (-1)^k.$$

This proves the result for $k + 1$ , so the general result is true by induction.

Corollary. Let $a_0, a_1, \ldots \in \real$ , where $a_0 \ge 0$ and $a_1, \ldots a_n > 0$ . Let

$$p_0 = a_0, \quad q_0 = 1$$

$$p_1 = a_1a _0 + 1, \quad q_1 = a_1$$

$$p_k = a_k p_{k - 1} + p_{k - 2}, \quad q_k = a_k q_{k - 1} + q_{k - 2} \quad\hbox{for}\quad k \ge 2.$$

Then $\dfrac{p_k}{q_k}$ is in lowest terms for $k \ge 1$ .

Proof. $p_k q_{k - 1} - p_{k - 1} q_k = (-1)^{k - 1} = \pm 1$ implies that $(p_k, q_k) = 1$ .

Example. The Golden Ratio $\dfrac{1 + \sqrt{5}}{2}$ has the infinite continued fraction expansion $[1; 1, 1, \ldots]$ .

(a) Find the first 10 convergents.

(b) Find an integer linear combination of 89 and 55 that is equal to 1.

(a)

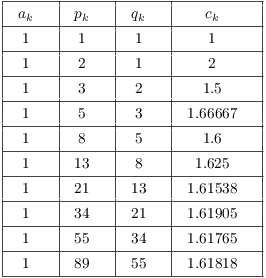
$$\vbox{\offinterlineskip \halign{& \vrule # & \strut \hfil \quad # \quad \hfil \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & \cr & $a_k$ & & $p_k$ & & $q_k$ & & $c_k$ & \cr height2pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & \cr & 1 & & 1 & & 1 & & 1 & \cr height2pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & \cr & 1 & & 2 & & 1 & & 2 & \cr height2pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & \cr & 1 & & 3 & & 2 & & 1.5 & \cr height2pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & \cr & 1 & & 5 & & 3 & & 1.66667 & \cr height2pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & \cr & 1 & & 8 & & 5 & & 1.6 & \cr height2pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & \cr & 1 & & 13 & & 8 & & 1.625 & \cr height2pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & \cr & 1 & & 21 & & 13 & & 1.61538 & \cr height2pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & \cr & 1 & & 34 & & 21 & & 1.61905 & \cr height2pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & \cr & 1 & & 55 & & 34 & & 1.61765 & \cr height2pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} height2pt & \omit & & \omit & & \omit & & \omit & \cr & 1 & & 89 & & 55 & & 1.61818 & \cr height2pt & \omit & & \omit & & \omit & & \omit & \cr \noalign{\hrule} }} $$

(You might have noticed that the p's and q's are the Fibonacci numbers!)

In fact, $\dfrac{1 + \sqrt{5}}{2} \approx 1.61803$ . In this case, you can see formally that $[1; 1, 1, \ldots]$ should be $\dfrac{1 + \sqrt{5}}{2}$ . Let

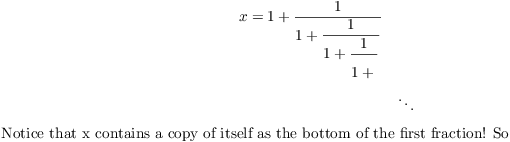
$$\raise0.38in\hbox{$x = $} \matrix{1 + \dfrac{1}{1 + \dfrac{1}{1 + \dfrac{1}{1 + \vphantom{\dfrac{1}{1}}}}} & \cr & \ddots \cr}$$ Notice that x contains a copy of itself as the bottom of the first fraction! So

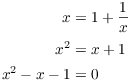
$$\eqalign{ x & = 1 + \dfrac{1}{x} \cr \noalign{\vskip2pt} x^2 & = x + 1 \cr x^2 - x - 1 & = 0 \cr}$$

The roots are $\dfrac{1 \pm \sqrt{5}}{2}$ . Since the fraction is positive, take the positive root to obtain $x = \dfrac{1 + \sqrt{5}}{2}$ .

(b) Applying the Theorem to the last two rows of the table, I have

$$34 \cdot 89 - 55 \cdot 55 = 1.\quad\halmos$$

Contact information

Bruce Ikenaga's Home Page

Copyright 2022 by Bruce Ikenaga